超外差式收音机的统调

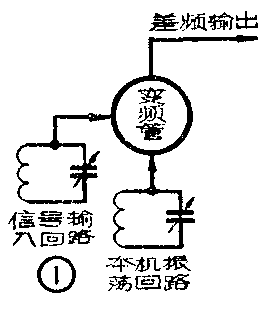
超外差式收音机的主要特点是它有一个变频级。这个变频级包括两个调谐回路（见图1），一个是信号输入回路。调节这个回路可以选择不同信号频率的电台；另一个是本机振荡回路，调节这个回路可以改变本机振荡器的振荡频率。振荡频率和信号频率之间的关系是：振荡频率永远高于信号频率，并且它们二者之差为一固定的中频。在我国，这个中频频率选用465千赫。例如当信号输入回路调谐到中央人民广播电台的640千赫时，本机振荡就应该调到640+465=1105（千赫）。同样的，当选择其他电台而调节信号输入回路时，也必须同时调节振荡回路的频率，以使两回路频率之差为一固定的中频，这就叫做超外差式收音机的统调，也叫跟踪调谐，意思是说，振荡回路的频率永远跟随着信号回路的频率而变化。

要求振荡回路频率与信号回路频率实现统调，在技术上是有困难的。下面我们以中波广播波段为例，来分析一下有些什么困难。

中波广播波段是550—1600千赫，因此收音机在中波波段的信号回路的调谐范围也应当是550—1600千赫。

通常我们把一个调谐回路所能调谐的最高频率与最低频率之比，叫做这个调谐回路的复盖系数。如果这个最高频率与最低频率是某一波段的最高频率与最低频率，那么它们二者之比就叫做波段复盖系数，用符号K来表示：

这样看来，收音机的信号回路在中波波段的波段复盖系数为

根据统调的要求，振荡回路的最低频率应该是550＋465=1015（千赫）；最高频率应该是1600＋465=2065（千赫）。所以振荡回路的波段复盖系数就是

由此可见，振荡回路与信号回路的波段复盖系数不相同。

波段复盖系数不同有什么问题呢？大家知道，调谐回路的谐振频率，决定于这个回路的电容量及电感量，它们的关系式为

如果只改变调谐回路的电容，而不改变电感，那么波段复盖系数与回路电容量有下列关系：

其中C\(_{最大}\)和C最小分别表示调谐回路的最大电容和最小电容值。由上述关系式可以看出，在一个波段内，振荡回路与信号回路的波段复盖系数不同，那么两个回路的C\(_{最大}\)与C最小的比值就不相等，它们分别从最低频率变到最高频率时，所要求的可变电容变化量也就不一样。因此，振荡回路与信号回路就必须用两种不同的可变电容来调谐，以使信号回路在中波段从550千赫连续地变到1600千赫时，振荡回路能够从1015千赫连续地变到2065千赫。这就给实现统调造成了困难。为了克服这个困难，一般说来有下列几种方法：

一个方法是将信号回路与振荡回路分别用两个旋钮来调两个电容。用一个旋钮调信号回路，找到欲收听的电台；然后再调振荡回路旋钮，得到准确的差频。但是这种方法既不方便，又难调得准确，并且结构也复杂，所以一般不采用。

另一方法是采用一只同轴双连可变电容器，因而只需要一个调谐旋钮。双连电容器的两组电容量不同，它们各自构成信号回路及振荡回路的调谐电容。为了使它们旋转到任何角度时，都能满足统调的要求，这两组电容器的极片必须经过特殊设计。但这种电容器也只能在一个波段内能满足统调的要求，对于多波段收音机就不适用了。

另外还可以固定两个回路的电容，而调节电感线圈的铁芯使两回路的电感量发生同步变化，以达到统调目的。但这种方法成本高，容易失谐，而且制作困难，也很少用。

目前广泛采用的方法是用一个旋钮，调节一个同轴双连可变电容器，这个双连电容器的两组电容量是相同的。为了达到统调的目的，在振荡回路里串联及并联微调电容。这种方法既简单、方便，又能满足统调的要求，这就是我们平常所说的“三点统调”。下面介绍它的工作原理。

在介绍三点统调的原理之前，我们先研究一下信号回路和振荡回路采用相同的调谐电容会产生什么影响。

上面已经谈到，信号回路与振荡回路的波段复盖系数不应该相等。如果电感不变，而两回路采用相同的可变电容，那么实际上它们的波段复盖系数是相等的，即：

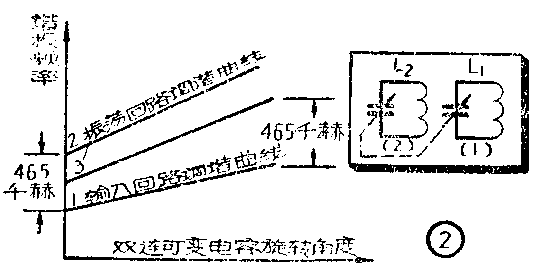
因此与上述要求违背。在这种情况下，信号回路的波段复盖系数决定于中波广播波段的频率，已知它近似等于3，因此信号回路电容的调谐范围必须满足这个数值。但是这样就使振荡回路的波段复盖系数也近似地等于3。如果使中波段的最低频率满足统调要求，即f\(_{振最小}\)=550＋465=1015（千赫），根据波段复盖系数的定义，振荡回路的最高频率就变成f振最大=3×1015=3045（千赫），远高于所要求的2065千赫。假设可变电容器的动片旋转角度（即电容量的变化）与谐振回路的频率成直线关系（这种假设符合实际情况），上述情况就如图2的曲线1和2所示，可以明显地看出来，振荡回路与信号回路除在最低频率处相差为中频以外，其他各点都不等于中频，而且频率越高离中频越远。同样，如果在中波波段的最高频率处满足统调要求，即振荡回路的最高频率f\(_{振最大}\)=1600＋465=2065（千赫），那么它的最低频率则为f振最小=2065/3=688（千赫），比要求的1015千赫低得多。这就是说，除了在f\(_{振最大}\)处两回路频率相差为中频外，其他各点都不等于中频。频率越低距中频越远，如图2的曲线1、3所示。我们还可以使振荡回路在其它某一个频率上与信号回路频率之差为中频，但是，在这种情况下也只能有这一点满足统调要求，其他各点都不能满足，离这点越远，偏差就越大。

为了解决在全波段内都满足统调要求的问题，可以采用在振荡回路里串联及并联微调电容的办法。

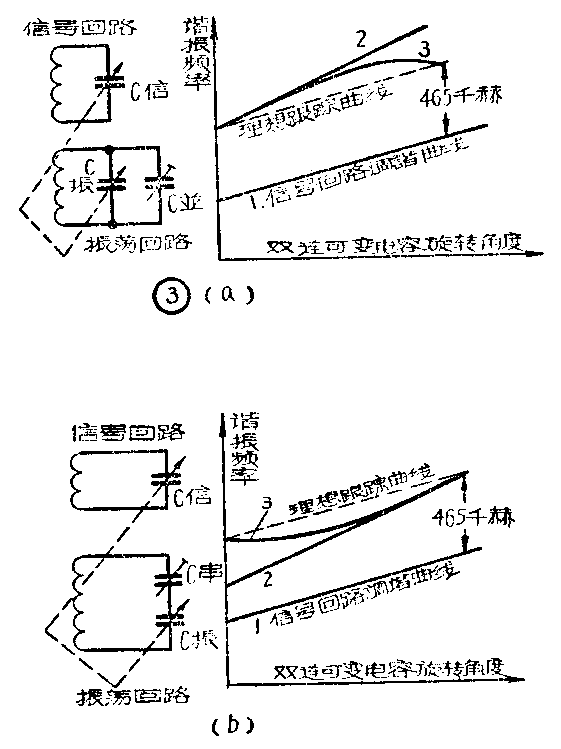
并联在振荡回路里的电容叫补偿电容（图3a的C\(_{并}\)）。图3a中曲线2是不加并联补偿电容时，振荡回路的调谐曲线，它在f振最小处满足统调要求。图中的理想跟踪曲线就是总保持两回路频率之差为中频的曲低。C\(_{并}\)的容量与C振的最小值相近，当振荡回路在最低频率时，C\(_{振}\)的值最大，这时C并远小于C\(_{振最大}\)，所以C并对回路电容几乎没有影响，因而对振荡回路的调谐频率也几乎没有影响。但是当回路频率升高时，由于C\(_{振}\)逐渐旋开，电容量逐渐减小，C并对回路电容的影响就逐渐显著，一直到C\(_{振最小}\)时，C并对回路电容的影响最大。这种影响的结果，便使振荡频率不随C\(_{振}\)的减小成直线上升，而是如图3a的曲线3所示。在上升中逐渐向下弯曲，因而可得一点与信号频率之差再次等于中频。

串联在振荡回路里的电容叫垫整电容（图3b的C\(_{串}\)）。图中曲线2是不加热整电容时，振荡回路的调谐曲线，它在最高频率处满足统调要求。C串的电容量与C\(_{振最大}\)相近，当振荡回路在最高频率时，C振的值最小。由于C\(_{串}\)远大于C振最小，所以C\(_{串}\)对回路电容几乎没有影响，因而对振荡频率也几乎没有影响。但是当C振逐渐增大时，即振荡频率逐渐下降时，C\(_{串}\)的影响就逐渐显著，其结果便使振荡频率不随C振的增大成直线下降，而是如图3b的曲线3所示，在下降过程中逐渐向上弯曲，因而在某一点与信号频率之差再次等于中频。

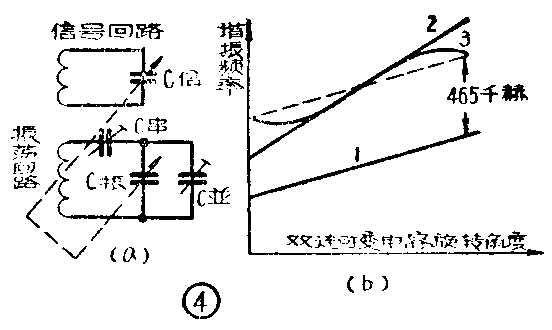
如果在振荡回路中只串联或只并联一个微调电容，那么就只有两点满足统调要求。但是，如果在振荡回路中同时并联及串联上述的微调电容（见图4a），而又使振荡回路在中间的振荡频率处满足统调要求，那么振荡回路的谐振曲线就是一个S形（图4b的曲线3），这个S形曲线很接近于理想曲线。在S形曲线中有三点是和信号频率刚好相差一个中频，其他各点则稍差一些，但也很接近于中频，所以这种方法称为三点统调。虽然在整个波段内只有三点完全符合要求，但由于中频变压器的通频带不是很窄，所以在实际运用中是完全允许的。

能不能再增加一些串并联电容，因而再增加几个准确跟踪点呢？不能了。因为串联或并联电容的数目虽然增加，归根到底也还是相当于串联及并联一个电容的作用，只不过是使准确跟踪点的位置移动罢了，而准确跟踪点的数目仍等于3。(荣田)