从一个现象谈起
在调试收音机的时候,我们会遇到这样的现象:电子管正常工作时,测得灯丝电压U\(_{L}\)是6.3伏(见图1a);假如把电子管拔下来,即让灯丝变压器的次级开路,再来测量这个电压(这样测得的电压叫做开路电压),就变成6.8伏左右了,这是什么原因呢?
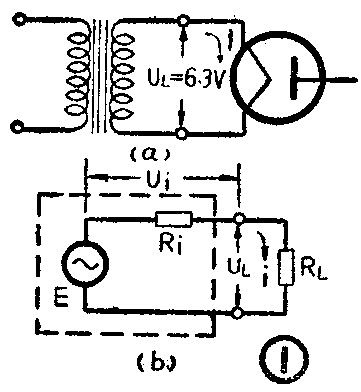
我们知道,对电子管的灯丝来说,灯丝变压器就是它的电源,这个电源的电动势等于灯丝变压器次级线圈的开路电压。同时我们还知道,变压器的次级线圈存在着电阻,虽然这个电阻的数值很小,只有零点几欧(因为次级线圈的圈数很少,所用漆包线也较粗),但是它在电子管的灯丝电路中却是不能忽略的。
图1b是电子管正常工作时的等效电路。E是电源电动势,R\(_{i}\)是变压器次级线圈的电阻,RL是负载(即电子管灯丝)。由图可见,在电子管正常工作时,由于回路电流在电阻R\(_{i}\)上也要产生一个电压降(Ui),因此,这时我们所测得的灯丝电压实际上等于电源电动势与次级线圈本身的电压降之差,即U\(_{L}\)=E-Ui,自然U\(_{L}\)的值是小于E的。
从这里可以看出,电子管正常工作时的灯丝电压比开路电压低,就是由于灯丝变压器次级线圈中存在着电阻造成的。而这个电阻一般叫做灯丝电源的内阻。
在无线电技术中,使用着各种各样的电源。例如,最常见的直流电源有电池、整流器等,最常见的交流电源有交流发电机、振荡器等。所有的电源,都有内阻。电源内阻的大小,在电路中起着很大的作用,在不同的场合,对它有着不同的要求。有些地方要求内阻越小越好;有些地方则相反地要求它越大越好;而另一些场合则要求大小适度。
越小越好
上面的例子要求电源的内阻越小越好,最好等于零。这样,电源电压就可以全部加到负载上。下面再举一些要求电源内阻越小越好的例子。
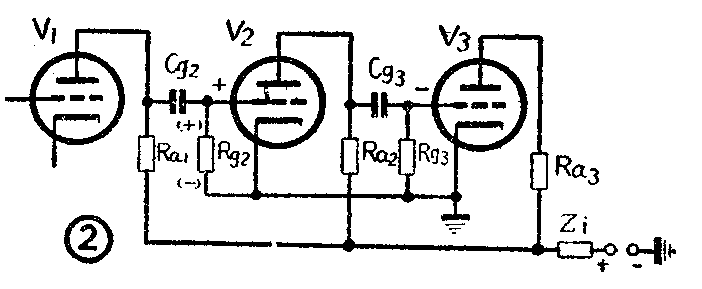
图2是一个三级电压放大器。电子管V\(_{1}\)、V2、V\(_{3}\)使用一个分共电源,该电源内阻为Zi。
假如V\(_{3}\)的屏流由于某种原因引起一个低频骚动,这个骚动电流就会在电源内阻Zi上产生一个电压降。如果Z\(_{i}\)的数值很大,这个电压降也就很大。这个电压经过高压线和偶合电容Cg2输送到V\(_{2}\)的栅极上。因为V3的输出和V\(_{2}\)的输入同相,所以是正反馈。这样就能产生低频自激,在收音机和扩音机中就形成卜卜的“汽船声”。
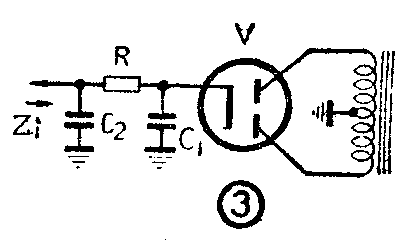
防止低频自激的最根本的方法,是减小电源的交流内阻Z\(_{i}\)。因此一般放大器的电源滤波器,最后一个电解电容(图3中的C2)往往选用很大的电容量,通常为几十微微法。这时电源的交流内阻就主要决定于该电容器的容量,因此变得很小。
有一种利用串联谐振来测量电感Q值的方法,这个方法也要求使用内阻很低的电源。例如图4,E代表一个振荡器的开路电压(设该振荡器的频率可变),R\(_{i}\)是振荡器的内阻,L和C接成串联电路作为负载(忽略L的电阻)。
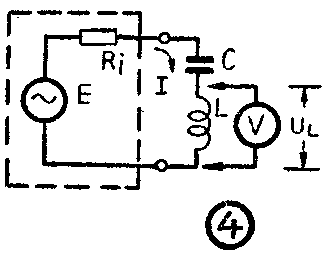
我们知道,L、C串联电路的阻抗是随频率而变化的。如果改变振荡器的频率,使L、C产生串联谐振,则负载阻抗为0,这时回路中就相当于只存在着电源内阻R\(_{i}\),因此回路电流(I=E/Ri)最大。假如振荡器的频率离开了谐振频率,则L、C在回路中就表现出一定的阻抗,因而使回路电流减小。振荡器的频率与谐振频率相差越大,则回路电流减小得越多。根据电路的这个特点,我们可以求出电感的Q值。因为在LC串联谐振时,在电感L两端的电压,也相应的有一个最大值U\(_{L}\)=QE(图4中用电压表V来指示),从这个电压的明显变化中,我们就能找到谐振点,并从公式Q=UL/E中求出电感的Q值。
如果振荡器的内阻R\(_{i}\)很大,那么谐振和不谐振时流过LC的电流就不会有明显地变化,这样就很难找到谐振点,因此Q值也就无法求出了。
越大越好
上面所举的例子,都是希望电源的内阻愈小愈好。但在另一些电路中,却希望电源内阻尽可能的大。
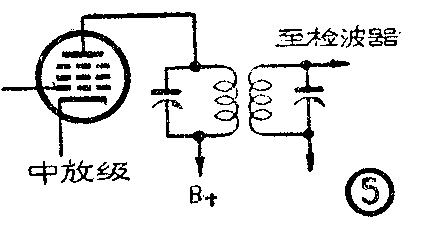
收音机中放级的中放管,对中频变压器来说就是一个交流电源(见图5)。如果这个电源的内阻很低,就会对回路产生并联作用,因而降低中频变压器回路的Q值,使收音机的选择性变坏,因此我们希望它有较高的内阻。通常中放级多采用五极管而不用三极管,其原因之一,就是因为五极管有较大的内阻。
有一种利用并联谐振测量电感或电容值的方法(被测电感或电容必须是低耗元件,使用这种方法测出来的数值才会准确),也是希望电源的内阻愈大愈好。
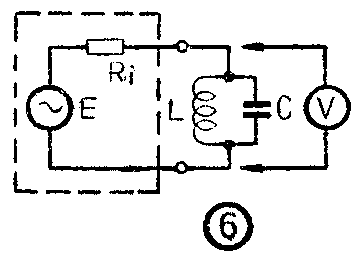
这种方法,是利用一个频率可变的振荡信号与一个LC并联回路相串联(如图6所示)。当LC并联回路谐振时,谐振频率为:
f\(_{0}\)=\(\frac{1}{2π}\)\(\sqrt{LC}\)
由此可以得到:
L=\(\frac{1}{4π}\)\(^{2}\)f\(_{0}\)2C;C=1;4π\(^{2}\)f02L
这就是说,如果预先知道了电容(或电感)的数值,就可以从上两个公式中求出电感(或电容)的数值。
使用这个方法得到准确结果的关键问题是必须准确地测出谐振频率f\(_{0}\)。如果电源的内阻很小,则在LC两端上的电压,不管是谐振或不谐振,都等于电源的开路电压E。也就是说不管在什么频率,电压表都指着一个不变的数,于是谐振频率就无法确定。
但是,如果电源的内阻很大,在没谐振时,LC的并联阻抗很小,电压表的指示也很小;当谐振时,因回路的谐振阻抗很大,LC两端就相应地有一个很大的电压,于是谐振频率就可以从电压表上准确地指示出来。
大小适度
有时候电源内阻既不能太大又不能太小,而是要求它有一个确定的数值。例如在通信方面,为了保证通信质量,常常要求电源的内阻和设备、线路的输入阻抗相等,即在阻抗匹配的情况下工作。这就要求电源的内阻有各种确定的数值,如6O0欧、150欧、75欧等等。
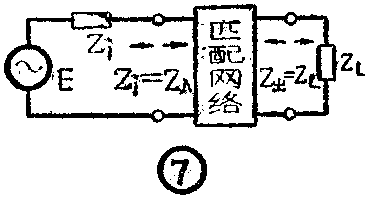
在许多场合,电源的内阻并不可能恰恰满足匹配的要求,往往不是电源的内阻高、负载阻抗低,就是电源内阻低而负载阻抗高。因此,我们常常把一些电抗网络、变压器、阴极输出器等接在电源和负载之间,使它们匹配(如图7所示)。
在功率放大级中也有匹配的要求。如在收音机的功率输出级中,负载是扬声器,而功率管的屏阻就相当于电源的内阻。因为扬声器的阻抗很低,一般只有几欧。而功率管的屏阻却很大,通常是几千欧。为了使扬声器获得较大的功率并减小失真,就必须采取匹配措施,这也就是使用输出变压器的原因。
由上述三种情况可见,不同的电路对电源内阻有不同的要求。有时大好,有时小好,有时却要求有一个确定的数值。我们应该根据不同的需要来选用电源。(方波)