多谐振荡器

在脉冲技术中，广泛地应用多谐振荡器来产生矩形波。由于矩形波中含有很多谐波，因而把这种振荡器叫做多谐振荡器。

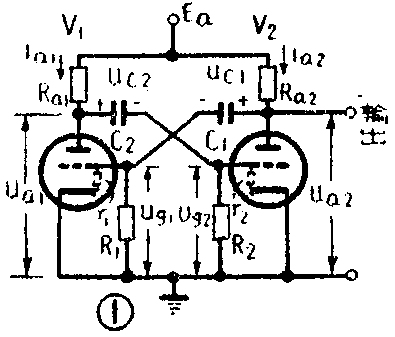
图1是多谐振荡器的基本电路，即所谓板极耦合多谐振荡器。从表面上看，这电路可能有一个稳定的平衡状态，即电子管的栅压为零，而两个管子中都通过很大的电流。但是，这种状态实际上是不可能存在的。因为图1电路实质上是一个具有强烈正反馈的二级放大器，电路中任何电流和电压的偶然变动，都会引起自激，把平衡状态破坏。

例如，设电子管V\(_{1}\)的栅压ug1由于某种原因稍有降低。于是V\(_{1}\)的屏流ia1减小，屏地ua1增加。由于C\(_{2}\)上的电压uc2不能跃变，所以u\(_{a1}\)的增加立即通过C2传到V\(_{2}\)的栅极，使ug2增高。或者换个说法，V\(_{1}\)的屏压ua1一增加，它就比C\(_{2}\)上的电压uc2高，因而C\(_{2}\)开始充电，充电电流流过R2，就使V\(_{2}\)的栅压Ug2增高。

U\(_{g2}\)一增高，电子管V2的屏流i\(_{a2}\)就增加，而屏压Ua2就减小。由于C\(_{1}\)上的电压Uc1不能跃变，所以U\(_{a2}\)的减小立即通过C1传到V\(_{1}\)的栅极，使ug1进一步降低。或者换个说法，u\(_{a2}\)一减小，C1就通过V\(_{2}\)和R1放电，放电电流是从R\(_{1}\)的下端流到上端，从而使V1的栅压进一步降低。

由此可见，V\(_{1}\)栅压的起始变化经过电子省V1、V\(_{2}\)的两级放大后，将有一个方向相同而数值被放大了的电压变化反馈到V1的栅极。这样就构成了自激的条件。u\(_{g1}\)一旦偶有降低，经过反铅将使ug1进一步降低；新的电压降低再一次经过V\(_{1}\)、V2的放大，反馈到V\(_{1}\)栅极，就使ug1更加降低。这样循环下去，就消成了一个雪崩式的跃变过程，u\(_{g1}\)急剧下降，达到很大的负值，使电子管V1截止。与此同时，u\(_{g2}\)则急剧上升，使电子管V2中通过很大的屏流。这样就转入了V\(_{1}\)截止、V2导电的状态。这个跃变过程的时间极短（不到一个微秒），在此时间内，电子管的栅压、屏压和屏流都是跃变的，而电容器两端的电压u\(_{c1}\)和uc2则几乎不变。

V\(_{1}\)截止后，ug1的变化就不能对u\(_{a1}\)发生影响，破坏了正反馈的条件，于是跃变过程结束，进入了缓变过程。在跃变过程中，ua1突然升高很多，但是u\(_{c2}\)上的电压未变，所以电源Ea将通过R\(_{a1}\)、C2、R\(_{2}\)以及V2的栅阴极间电阻r\(_{2}\)向C2充电。到充电完了时，u\(_{a1}\)=uc2=E\(_{a}\)，而ug2=0，于是V\(_{2}\)的屏流基本上等于零栅压所确定的电流I02，而u\(_{a2}\)=Ea-I\(_{0}\)2Ra2。另一方面，在跃变过程中，u\(_{a2}\)突然下降很多，而uc1未变，所以电容器C\(_{1}\)将通过电子管V2和R\(_{1}\)放电，正是这个放电电流在R1上的电压降，给V\(_{1}\)造成了很大的负栅压，使V1截止。V1截止后，这个放电电流逐渐减小，u\(_{g1}\)逐渐升高。但是在ug1未达到V\(_{1}\)的截止栅压Eg01以前，V\(_{1}\)一直保持在截止状态。这时两电子管的屏压和栅压，如图2中各曲线在t1以前时的情况所示。

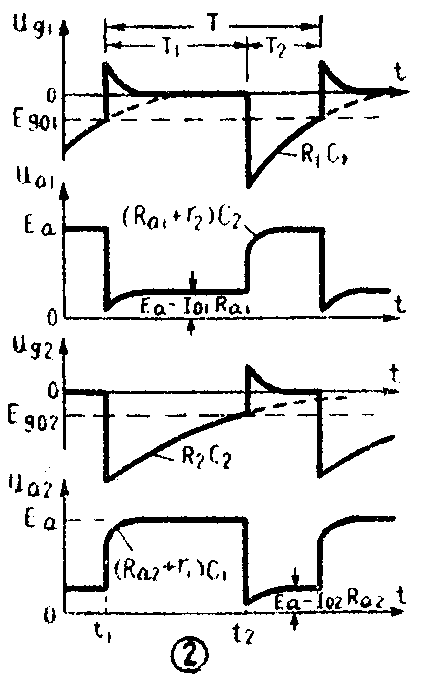
当u\(_{g1}\)上升到Eg01时（图2中的t\(_{1}\)瞬间），V1开始导电，u\(_{a1}\)降低，并立即通过C2的耦合使u\(_{a2}\)降低，于是V2屏流减小，u\(_{a2}\)增高，并立即通过C1的耦合使u\(_{g1}\)进一步上升。这样就构成了正反馈的条件，电路中又发生了雪崩式的跃变过程。这一次是ug2突然降低到很负的电压，使V\(_{2}\)截止，而ug1上升到很高的正电位，使V\(_{1}\)通过很大的屏流。即电路从V1截止、V\(_{2}\)导电的状态，突然翻转到V2截止、V\(_{1}\)导电的状态。随后跃变过程停止，开始了缓变过程。这时由于ua2突然上升，E\(_{a}\)将通过Ra2、R\(_{1}\)以及V1的栅阴极间电阻r\(_{1}\)向C1充电。而由于u\(_{a1}\)突然下降，C2开始通过V\(_{1}\)及R2放电。放电电流在R\(_{2}\)上产生电压降，使ug2具有很大负值，从而使V\(_{2}\)截止。

之后，C\(_{2}\)的放电电流逐渐减小，ug2升高，当达到V\(_{2}\)的截止栅压Eg02时（图2中t\(_{2}\)瞬间），V2导电，又开始了另一个雪崩过程，u\(_{g2}\)突然升高，ug1突然下降到截止栅压以下，电路又翻转到V\(_{1}\)截止、V2导电的状态。就这样，电路不断转换地从一个状态转入另一个状态，两个电子管交替地截止和导电，C\(_{1}\)和C2交替地充电和放电，使振荡一直维持下去，在两个电子管的屏极得到了近似的矩形波。

多谐振荡器所输出矩形波的波形，和电容器的充电有很大关系，而矩形波的周期则决定于电容器的放电过程。

前面讲过，在图2中的t\(_{1}\)瞬间，电子管V2突然截止，u\(_{a2}\)突然增加，V1的栅压突然增高到正值。这时E\(_{a}\)通过Ra2、R\(_{1}\)和V1的栅阴极间电阻r\(_{1}\)向C1充电。充电电流在R\(_{a2}\)上产生一个电压降，因此V2的屏压U\(_{a2}\)不是在V2经跃变而截止时立刻就等于电源电压E\(_{a}\)，而是随着C1的充电而逐渐上升，到C\(_{1}\)充电完毕后才能等于Ea。这样，就在输出矩形波的上角形成一个圆角，如u\(_{a2}\)曲线在t1时的情况所示。

另一方面，在跃变期间，V\(_{1}\)的屏压ua1下降到什么地步，要决定于栅压u\(_{g1}\)。在跃变时，ug1达到最大正值，i\(_{a1}\)最大，ua1降到最低值。以后，由于C\(_{1}\)的充电电流逐渐减小，ug1g1逐渐下降到零，屏流i\(_{a1}\)逐渐趋于零栅压所确定的电流I01。与此相应，屏压u\(_{a1}\)逐渐上升，到C1充电完毕时，达到u\(_{a1}\)=Ea-I\(_{0}\)1Ra1的数值，稳定下来。这样就在矩形波的下角形成一个尖角，如图2中u\(_{a1}\)曲线在t1时的情况所示。

由此可见，电容器充电越快，输出电压就越接近于矩形。充电的快慢决定于充电电路的时间常数。由于栅阴电阻r\(_{1}\)和R1并联，同时又甚小于R\(_{1}\)，所以R1的作用可以忽略。充电电路的时间常数为（R\(_{a2}\)＋r1）C\(_{1}\)。为了增大充电速度，应选取小的Ra2值和C\(_{1}\)值。但是Ra2不能小于1千欧，否则输出矩形波的幅度要减小很多，同时由于电子管的放大系数减小，跃交的持续时间增加，影响前后沿的陡度。一般R\(_{a}\)用几千欧到几十千欧。C1也不能小于100微微法，否则寄生电容将会对多谐振荡器的工作发生显著影响。上述情况也适合于C\(_{2}\)的充电电路和C2、R\(_{a1}\)的选择。

从前节的叙述还可以看到，V\(_{1}\)从开始导电到重新截止的时间，或者说V2保持截止的时间T1（见图），决定于C\(_{2}\)放电的速度。C2放电越快，u\(_{g2}\)就更早地上升到Eg02，使V\(_{2}\)重新导电。C2放电电路的时间常数为（R\(_{2}\)+Ri1）C\(_{2}\)，其中Ri1为电子管V\(_{1}\)的内阻。由于R2甚大于R\(_{i1}\)，所以可以近似地认为这个时间常数等于R2C\(_{2}\)。选择 R2C\(_{2}\)的乘积，就可以获得所需的矩形波宽度T1。同理，C\(_{1}\)放电电路的时间常数R1C\(_{1}\)确定了电子管V2导电（V\(_{1}\)截止）的持续时间T2。

栅极电阻R的数值通常约为几百千欧。

经过计算可以近似地得到，在振荡频率不太高的情况下，

多谐振荡器振荡的总周期T=T\(_{1}\)+T2。

如果电路是对称的，即采用同型号的电子管，而R\(_{a1}\)=Ra2，C\(_{1}\)＝C2，R\(_{1}\)=R2，那么输出的矩形波也将是对称的，周期T1=T2。这种多谐振荡器称为对称多谐振荡器。

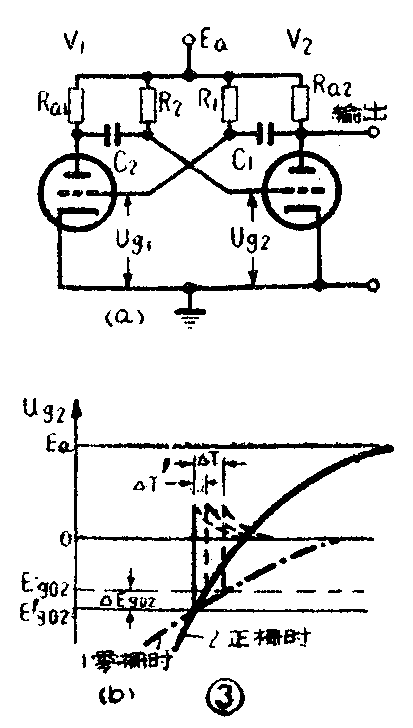
由于振荡器的周期（或频率）决定于截止管栅压上升曲线和该管截止栅压线的交点，所以电子管的截止栅压是否稳定，对振荡频率的稳定性有很大影响。例如，当电子管V\(_{2}\)的截止栅压Eg02因电源电压变化或其他原因而变化一个数值ΔE\(_{g}\)02时（参看图3b），ug2上升曲线1和截止栅压线E\(_{g}\)02的交点就要延迟ΔT的时间，也就是使振荡周期加长ΔT的时间。相似地，V1截止栅压E\(_{g}\)01的变化也会使振荡周期改变。为了减小截止栅压的变化对振荡周期的影响，常采用图3a所示的“正栅”电路，即两个栅极电阻不是接地，而是接到电源正极。这个电路和前面所讲的“零栅”电路的工作基本上相同。不同的是，当发生跃变时，例如V1突然导电和V\(_{2}\)突然截止时，C2不是像零栅电路中那样通过V\(_{1}\)和R2放电，力图使u\(_{g2}\)上升到零（图3b中曲线1），而是由电源Ea经过R\(_{2}\)和V1对C\(_{2}\)反向充电，力图使ug2从很大的负值上升到正E\(_{a}\)（图3b中曲线2）。这样，曲线2就比曲线1陡得多，当Eg02变化ΔE\(_{g}\)02时，曲线2和E′g02线的交点只延迟较短的时间ΔT′。由此可见，“正栅”电路所产生振荡的周期受E\(_{g}\)0变动的影响较小，也就是振荡频率要稳定一些。

在正栅电路和零栅电路元件相同的条件下，由于前一电路中电容器反向充电较快（图3曲线2），所以截止管的栅压（例如u\(_{g2}\)）将在较短时间内上升到截止栅压，引起跃变。因此，正栅电路所产生振荡的周期较短，或者说振荡频率较高。

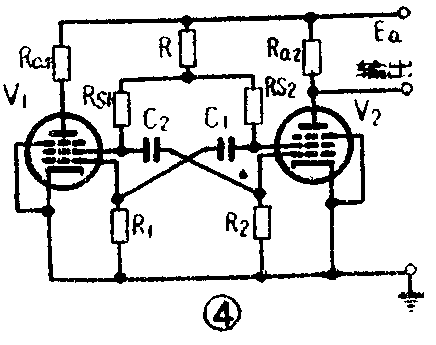
实际中常常采用五极管接成多谐振荡器，电路如图4所示。这里把帘栅极用作为多谐振荡器的屏极。当多谐振荡器工作时，通过电子管屏流的变化，屏压就重复着帘栅压的变化，输出矩形波。五极管多谐振荡器的好处是：第一，抑制栅极把屏极和其他电路部分屏蔽起来，因而负载的变化不会严重影响振荡器的工作，不会影响到振荡波形和频率。第二，因为耦合电容器没有接到屏极。所以当电子管截止时，电容器的放电电流不会流过屏极电阻，屏压可以立即跃变到电源电压E\(_{a}\)，即矩形波的左上角不会出现圆角，因而可以输出更加接近于矩形的电压。(黎明)