由电阻R和电感L组成的电路(简称RL电路),和第6期介绍过的RC电路一样,也在脉冲技术中获得了广泛的应用。这种电路和RC电路有很多相似或相对应的地方。把两者对照着看,就不难了解RL电路中的瞬变过程了。
电感线圈中的电流不能跃变
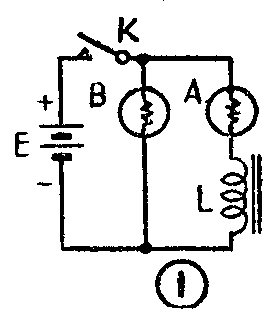
我们先来作一个实验。按照图1接成一个电路。电路中A、B两个电灯完全相同,不过在A灯支路中串接一个电感很大的线圈L。当合上开关K时,B灯立刻燃亮,而A灯却由暗逐渐变亮,经过一段时间才能达到和B灯一样的亮度。什么原因呢?
大家都知道电感线圈有自感作用。当外加电压发生变化,从而要迫使电感支路中的电流发生变化时,电感L中就产生一个反电动势,力图阻碍电流的变化。因此,电感线圈L中的电流不能跃变,只能随时间逐渐变化,就和电容器C上的电压不能跃变的情况相似。A灯逐渐变亮的情况,就是反映了电感的这个重要特性。
还可以从能量观点说明电感L中的电流不能跃变。设电感线圈L中的电流为i\(_{L}\),则线圈周围储存的磁能为WL=\(\frac{1}{2}\)Li\(^{2}\)\(_{L}\)。因为能量的积累或耗散,需要经过一定时间,不能跃变,因而从上式可以看出,和磁能密切联系着的电流也只能逐渐改变,不能跃变。
RL电路中的瞬变过程
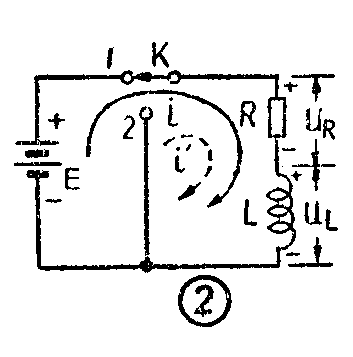
现在进一步讨论RL电路中电流和电压变化的情况。我们看一下图2。在开关K未接到点1以前,电路中没有电流,i=0。当K刚一关闭的瞬间(t=0的瞬间),由于 L中的电流不能跃变,i仍等于0(图3a)。所以电阻R上的电压降u\(_{R}\)等于0(图3b),整个电源电压都加到了L上,即L上的电压uL由0跃变到E(图3c)。换句话说,在t=0的瞬间,在电感L中产生了一个等于电源电压E的反电动势。以后,随着电流i的逐渐增长,R上的电压降u\(_{R}\)就逐渐增大,而L上的电压uL就逐渐减小。最后,电流i增加到\(\frac{E}{R}\),整个电源电压E都降落在电阻R上,L两端的电压u\(_{L}\)=0,电路就达到了新的稳态。各个电压和电流随时间变化的情况如图3所示。
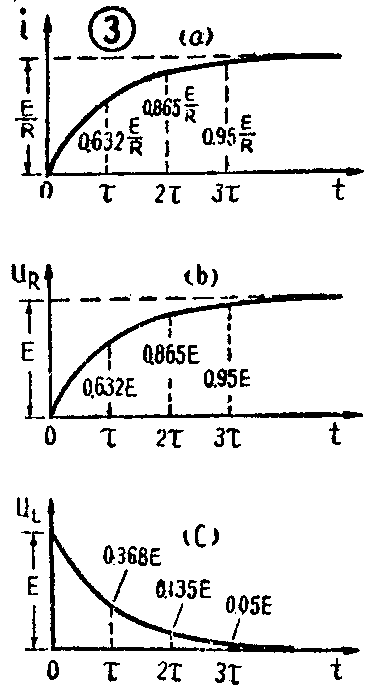
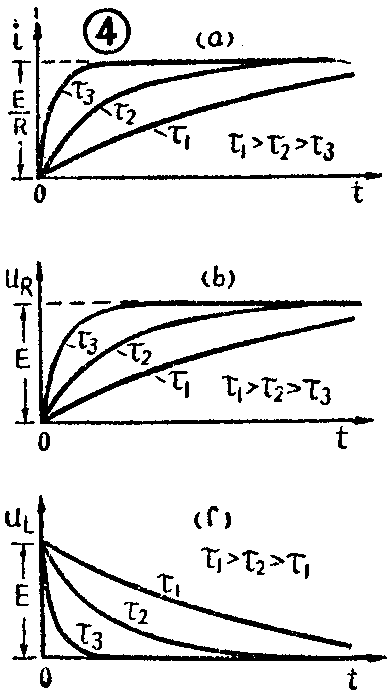
i、u\(_{R}\)增加的速度和uL减小的速度,决定于L和R的比值\(\frac{L}{R}\)。和乘积RC一样,L;R也是一个代表时间的数值。为什么呢?大家知道,电感L的电抗x\(_{L}\)=2πfL, 其中xL的单位是欧,L的单位是亨,f的单位是赫,即\(\frac{1}{秒}\)。由此可见,L=x\(_{L}\);2πf的单位可以表成\(\frac{欧}{1/秒}\)=欧·秒,而R的单位是欧,所以L;R的单位就是\(\frac{欧·秒}{欧}\)=秒了。数值L;R叫做RL电路的时间常数,也用字母τ表示。τ=\(\frac{L}{R}\)越大,i、uR的增加和u\(_{L}\)的下降就越慢,到达新的稳态所需的时间就越长。我们可以这样粗略地想像:L越大,反抗电流变化的能力就越强,电流的增长就越慢;R越大,电流i在电阻R上产生的压降就越大,电流有很小的增加就使R两端的压降增加很多,或者说使L上的电压下降很多,所以能够更快地达到稳态。因此,L越大,时间常数τ越大;相反地,R越大,时间常数τ越小。图4画出了在不同τ值下,电流、电压随时间变化的曲线。由图可见,如果τ=L;R很大(例如等于τ1),电流和电压的变化就很缓慢。如果τ=LR很小(例如等于τ\(_{3}\)),电流和电压的变化就较快。
理论证明,电流i、电压u\(_{R}\)和uL随时间t的变化可用下列公式表示
式中e\(^{-}\)\(\frac{t}{τ}\)是y=ex形式的指数函数,这里x=-t;τ是自变数,e≈2.72是自然对数的底。
从这些公式可以看到,当t=0时,e\(^{-}\)\(\frac{t}{τ}\)=e°=1,因而i=0、 u\(_{R}\)=0,uL=E。当t=τ时,e-t;τ=e\(^{-}\)1=\(\frac{1}{e}\)=0.368,因而i=(1—0.368)E;R=0.632\(\frac{E}{R}\),u\(_{R}\)=0.632E,uL= 0.368E(参看图3)。t=2τ时,e-t;τ=e\(^{-}\)2=\(\frac{1}{e}\)2=0.135,因而i=(1-0.135)E;R=0.865\(\frac{E}{R}\),u\(_{R}\)=0.865E,uL=0.135E。t=3τ时,e\(^{-}\)t;τ=e-3=\(\frac{1}{e}\)\(^{3}\)=0.05,因而i=(1-0.05)E;R=0.95\(\frac{E}{R}\),u\(_{R}\)=0.95E,uL=0.05E。……最后,只有当t=∞时,才能使e=-t;τ=e\(^{-}\)∞=\(\frac{1}{e∞}\)=0,从而使i=E;R,u\(_{R}\)=E,uL=0。
时间常数τ就是电流i从零增长到最后稳态值ER的0.632倍所需的时间,或者说是u\(_{L}\)。从起始值E下降到0.368E所需的时间。
从理论上说,只有经过无限长的时间以后,才能达到新的稳态。但是,当t=3τ时,电路中的状态即已和稳态很接近,所以实际上可以认为当t>3τ时,电路已达到新的稳态。
现在设电路已达稳态,电流i等于ER,u\(_{L}\)=0。如果忽然把图2中的开关K从1扳到2,电路中的瞬变过程又是怎样呢?
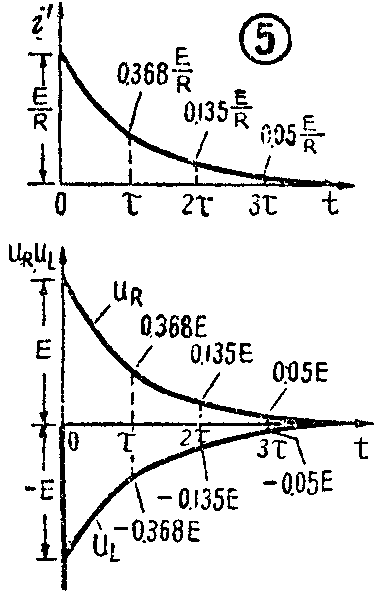
由于L中的电流不能跃变,所以当K刚扳到2的瞬间,即t=0时,新电路中的电流i'仍等于\(\frac{E}{R}\),电阻R上的电压仍等于E。这时L的两端直接和R的两端相连,所以L两端的电压和R两端的电压相同,不过这时L的下端为正,上端为负,所以它两端的电压为-E。这也就是电感L由于阻止电流减小而产生的反电动势。用来维持电流i'的是原先在L中储存的磁能W\(_{L}\)=1;2Li\(^{2}\)。i'流过R时将消耗能量,所以L中储存的磁能逐渐减小,i'也随着减小,uR和u\(_{L}\)都逐渐下降。最后,L中的磁能消耗完了,i'减小到0,uR和u\(_{L}\)也都下降到0。图5示各电流和电压随时间变化的情况。
电流和电压下降的快慢,也决定于时间常τ=\(\frac{L}{R}\)。L;R越大,下降越慢;LR越小,下降越快。
理论证明,在这种情况下,电流i'和电压u\(_{R}\)、uL随时间而变化的关系式如下:
i'=\(\frac{E}{R}\)e\(^{-}\)t;τ,
u\(_{R}\)=Ee\(^{-}\)\(\frac{t}{τ}\),
u\(_{L}\)=-Ee\(^{-}\)\(\frac{t}{τ}\)。
从这些公式可以看到。当t=0时,e\(^{-}\)
RL微分电路
在图6的RL电路中,加在输入端的不是直流电源E,而是一连串矩形脉冲。电路的时间常数τ=LR甚小于脉冲持续时间t\(_{i}\)。我们从L的两端取得输出电压。当脉冲到来时,输入电压从0跃变到脉冲幅度电压。由于电路中的电流不能跃变,R上的压降为0,所以这时L上的电压也随着跃变到U。但是由于τ=L;R甚小于ti,所以L上的电压随即下降到零,从而在输出端得到一个短脉冲。以后,输出电压即保持为0,而电路中的电流等于\(\frac{U}{R}\),R上的压降为U。直到脉冲终止时,输入电压突然变为零,相当于输入端短路。根据前面的分析,这时,L两端的电压突然从0跃变到-U。又因为时间常数τ=L;R很小,这个电压随即减小到0, 从而在输出端产生一个负的短脉冲。由此可见,这种电路和RC微分电路一样, 也能把输入的矩形波变成一连串正负交替的短脉冲。正脉冲和矩形波的前沿相应,负脉冲和矩形波的后沿相应。可见这也是一种微分电路,称为RL微分电路。它和RC微分电路一样, 需要具有很小的时间常数τ。不过要注意,由于这时τ=\(\frac{L}{R}\),所以要求R越大越好。而RC微分电路中由于τ=RC,所以要求R越小越好。另外,这里输出电压是从L上取得的。而在RC微分电路中,输出电压则是从R上取得的。
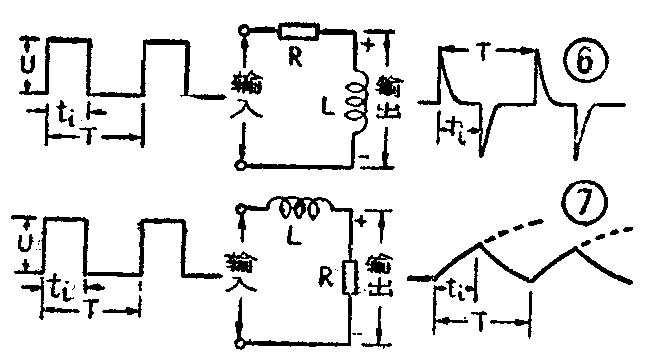
RL积分电路
图7示RL积分电路。它要求时间常数τ=\(\frac{L}{R}\)甚大于脉冲持续时间t\(_{i}\)(要求有很大的电感L和很小的电阻R),同时,输出电压是从R两端取得的。这样,当输入的矩形脉冲开始时,电路中的电流以及R两端的电压将在整个脉冲持续时间内缓慢地增长。当R两端的电压还没有增长到U时,脉冲即已终止。脉冲终止后,由于电感L的作用,R中的电流及其两端的电压又缓慢下降,结果就在电路输出端获得如图中所示的锯齿波。
可以看到,在RL积分电路中,电感L中的电流也是锯齿形的。因此,在有些场合中, 可用这种电路来产生锯齿形电流。例如在电视接收机中,就常采用这种电路的原理以在偏转线圈中得到锯齿形扫描电流。(黎明)