本文介绍产生正弦波的面接合型晶体管反馈振荡器的特点和电路。
晶体管的振荡特性
我们知道,晶体管的运用受到频率的限制。表征频率特性的最重要参数是电流放大系数α随频率而变化的关系。电流放大系数α下降至0.707倍时的频率称为截止频率f\(_{α}\)。例如П6A型晶体管的fα=100千赫,П6Г型晶体管的f\(_{α}\)=1000千赫等。
表征晶体管的振荡特性有一个更常用的参数,这就是最高振荡频率f\(_{最大}\)。它说明晶体管作为振荡器应用时,在最好条件下所能达到的最高频率。例如П401的最高振荡频率f最大=30兆赫,П402的f\(_{最大}\)=60兆赫,而П403的f最大=120兆赫。
最高振荡频率与截止频率之间的相互关系比较复杂。一般地说,对于用合金法制成的晶体管如П6、П13等,f\(_{最大}\)≤2fα。对于用扩散法制成的晶体管,如П401—403等,f\(_{最大}\)≤(3~4)fα。
最高振荡频率只说明了最大的可能性。现在要问,在低于最高振荡频率下,晶体管的振荡性能是怎样的。在低于最高振荡频率下,一般晶体管的功率增益系数K\(_{p}\)与最高振荡频率f最大之间的关系可近似表示为
K\(_{p}\)=(f最大f)\(^{2}\)。
这个公式表明,晶体管功率增益与工作频率的平方成反比例。在f=f\(_{最大}\)时,功率增益Kp=1。换句话说,最高振荡频率是功率增益等于1时的频率,在此频率下,晶体管只能维持振荡而没有功率输出。当频率低于最高振荡频率时,功率增益才会有显著的增加。例如在f=\(\frac{1}{2}\)f\(_{最大}\)时,Kp=4倍,在f=1;4f\(_{最大}\)时,Kp=16倍。以上的关系在f>0.1f\(_{最大}\)时一般是正确的。在甚低的频率下,低频功率增益约保持不变。各晶体管之间的低频增益差别很大,其数值在30—40分贝(1000—10000倍)之间变动。
对于实际应用来说,希望最少保持功率增益在10分贝(即10倍)以上,这时候才能够从振荡器取得必要的功率输出。这意味着,作为振荡器运用时晶体管应该工作在低于13f\(_{最大}\)的频率。例如,我们要做一部广播波段550—1600千赫的超外差收音机,中频为465千赫,则本机振荡频率应为1015—2065千赫。如用П6Г型晶体管作本机振荡器,则因fα=1000千赫,f\(_{最大}\)≤2fα=2000千赫,而1;3f\(_{最大}\)≤660千赫,所以一般说来是不适宜的。如果用П401—403作本机振荡器,由于fα很高,效果就很好了。
至于电子管,它的振荡特性的频率关系在很大范围内是不变化或者变化很小的。尽管它们在低频时的功率增益不如晶体管的功率增益那样大,但是它们在高频时仍能保持足够大的功率增益,这点比晶体管优越。
晶体管反馈振荡器的构成
反馈振荡器基本上由三部分组成(图1)。1)晶体管:它作为反馈放大器之用,能够将小功率的输入信号放大成为大功率的输出信号;2)振荡回路;它在某个频率下谐振;3)反馈回路:它将输出信号以适当的幅度和相位反馈至输入端。由此可见,晶体管振荡器与电子管振荡器在基本原理上是相同的。
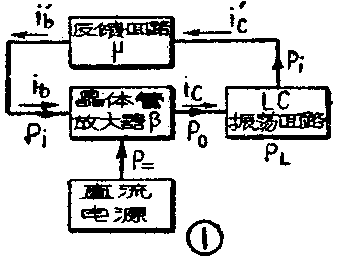
具有功率增益系数K\(_{p}\)的晶体管放大器把输入功率Pi放大成为总输出功率P\(_{0}\):
P\(_{0}\)=KpP\(_{i}\)。
总输出功率的一部分功率P\(_{L}\)输送至振荡回路(有用的输出功率)。另一部分功率Pi经反馈回路送入晶体管的输入端(反馈功率)。振荡回路所得到的有用的输出功率等于
P\(_{L}\)=P0-P\(_{i}\)=P0(1-\(\frac{1}{K}\)\(_{p}\))=P0(K\(_{p}\)-1;Kp)。
上式说明,如果晶体管的功率增益愈大,有用输出功率P\(_{L}\)也愈大。如果晶体管的功率增益接近于1,则有用的输出功率就接近于零。
振荡回路一般是用电感和电容构成的L\(_{C}\)回路,它的固有频率等于f0=12π\(\sqrt{LC}\)。在实际的振荡回路内,不可避免地会有一些能量损失。另外我们还要从振荡回路内取出必要的能量作为输出的能量,这是我们制作一个振荡器的实际目的。这两部分能量都是由晶体管的有用输出功率PL来供给的,因此振荡回路内的能量损失应力求减少。
反馈回路是将输出功率P\(_{0}\)的一部分(Pi)输送至晶体管的输入端。对于晶体管来说,反馈回路应该根据联接电路的不同而有所变化,它必须保证输出电流式输出电压以适当的相位和适当的比例输送至输入端。
反馈电流的大小很容易算出,例如对于共发射极联接的振荡器,晶体管本身具有电流放大系数β=\(\frac{i}{_{c}}\)ib(其中i\(_{c}\)=集电极电流,ib=基极电流,β=α/1-α,α=共基极联接的电流放大系数),反馈回路的反馈比μ=i'\(_{b}\);i'c,其中i'\(_{b}\)是反馈的基极电流,i'c是反馈的集电极电流。很明显,如果i'\(_{b}\)>ib,即反馈的基极电流大于维持放大状态的基极电流,就能够维持振荡。如果i\(_{c}\)=i'c,即放大后的集电极电流全部转换成反馈的集电板电流,则i'\(_{b}\)>ib的条件可改写成\(\frac{i'}{_{b}}\)i'c>i\(_{b}\);ic,也就是μ>1/β,这就是产生振荡的条件,或称起振条件。相似地可以推出,对于共基极联接的振荡器,如果μ>\(\frac{1}{α}\)即可产生振荡。反馈电流太大是不必要的,否则有用的输出电流(或者有用的输出功率)会相应降低。对反馈电流的要求是适可而止,只要使反馈比稍大于1/β或1/α就足够了。振荡回路与反馈回路有时候是由同一回路来构成的。
我们知道,共发射极电路的晶体管的输出信号与输入信号的相位是相反的,共基极电路和共集电极电路的输出信号与输入信号的相位是相同的。因此共发射极的振荡器的反馈回路应保证有180°的相移,共基极振荡器的反馈回路可以没有相移。
几种常用的晶体管振荡电路
以上我们介绍了晶体管振荡器的基本原理,现在再看一些实例。
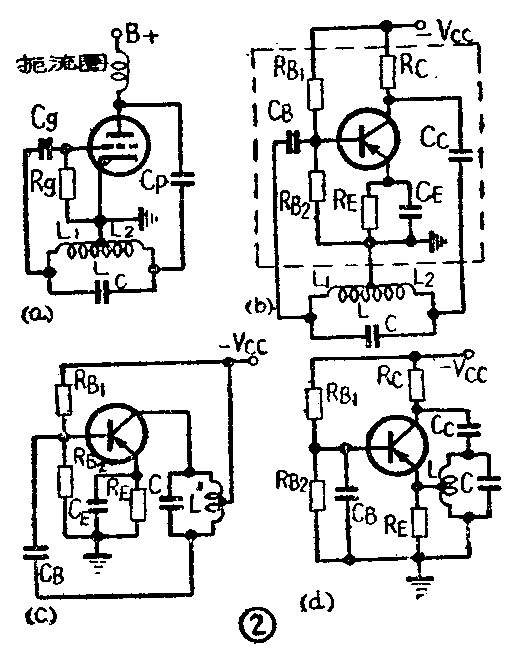
1.自偶变压器反馈式振荡器(哈特来振荡器)并联供电的共阴极电子管哈特来振荡器如图2a所示。并联供电和串联供电的共发射极晶体管哈特来振荡器如图2b和2c所示。图2b虚线方框内的晶体管是一个标准形式的共发射极放大器。供给集电极电压的电阻R\(_{c}\),可用高频扼流圈代替。电阻RB1、R\(_{B2}\)和RE用来建立稳定的直流工作点,C\(_{B}\)和CE对交流是短路的。振荡回路由电感L和电容C构成,它是集电极的交流负载。反馈回路的180°相移由自耦变压器形式的电感L提供,反馈比由L\(_{1}\)/L2决定,这里互感分别考虑在L\(_{1}\)和L2之内。
从图2a与2b的比较可知,晶体管振荡器与电子管振荡器在形式上和原理上有许多相似之处,但也有某些不同的地方。首先,电子管振荡器的栅偏压是由C\(_{g}\)Rg和栅极阴极的整流作用产生的,这样做有许多优点。而晶体管发射极的正向偏流是由直流电源供给的。其次,由于晶体管的输出阻抗比电子管的输出阻抗低,而且输入阻抗更低,增加了对振荡回路的负载。此外,晶体管在较高频率运用下,应该考虑到电流放大系数随频率的相移,反馈回路的设计要复杂一些。最后,由分析求得振荡频率f=12π\(\sqrt{LC}\)-k,式中k是与电感量和晶体管参数有关的量。为了获得频率的稳定,应该选择LC》k,亦即应在较低的频率下运用,并保持直流工作状态的稳定。看来,晶体管振荡器的频率稳定问题比电子管振荡器的要复杂一些。
共基极联接的哈特来振荡器如图2d所示。共发射极和共基极联接的振荡器在本质上是没有分别的。
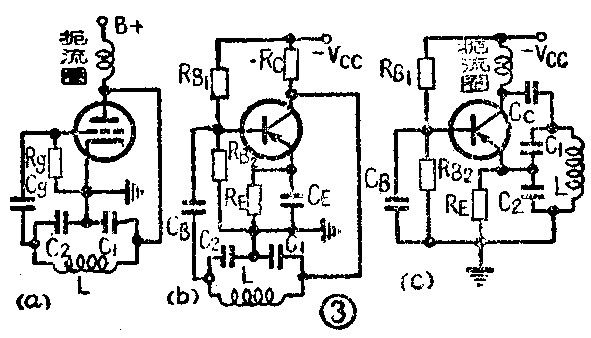
2.电容反馈式振荡器(科尔毕兹振荡器)并联供电的共阴极电子管科尔毕兹振荡器如图3a所示。并联供电的共发射极晶体管科尔毕兹振荡器如图3b所示。与哈特来振荡器比较, 科尔毕兹振荡器用电容反馈代替了电感反馈,反馈比等于C\(_{1}\)/C2。这种振荡器在调整上复杂一些,但是它的波形较好。以上关于哈特来电路的许多解释在这里仍然起作用。然而,这里振荡频率f=12π\(\sqrt{LC+k'}\), 式中k'是与电容量和晶体管参数有关的量。为了获得频率的稳定,要求LC》k'。
共基极联接的科尔毕兹振荡器如图3c所示。
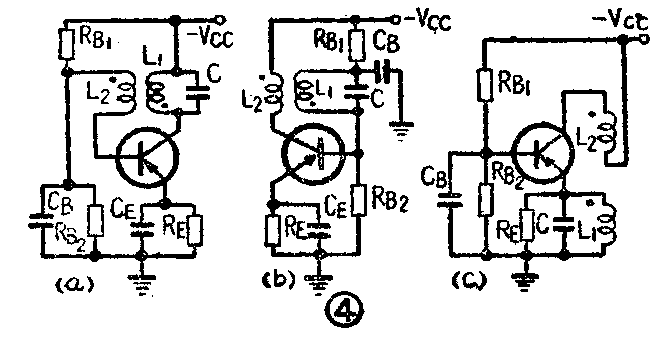
3.互感反馈式振荡器 调谐回路接在集电极电路内的电路(图4a)称为调集电极振荡器。实际上可以把它看成是哈特来振荡器的变形,这里不用电感L的自偶变压器抽头方法,而分成两个线圈L\(_{1}\)和L2的互感方法。这是一个共发射极电路。为了获得180°的相移,L\(_{1}\)和L2的联接方向是相反的。其它分析与哈特来电路完全相同。
调基极的振荡器(图4b)与调集电极的振荡器没有很大差别,它的振荡回路接在基极,反馈线圈接在集电极,并且有180°的相移。
调发射极的振荡器(图4c)在收音机的变频器里经常使用。这是一个共基极电路。它的振荡回路接在发射极,反馈线圈在集电极,两个线圈是同相的,因为在共基极联接时集电极电压与发射极电压的相位相同。
4.推挽式振荡器 推挽式晶体管振荡器如图5所示。它是由两个图4a的调集电极电路组成的,调整R\(_{B1}\)RB2和R\(_{E}\)可以使振荡器工作在甲类或乙类,因而产生更大的输出功率。
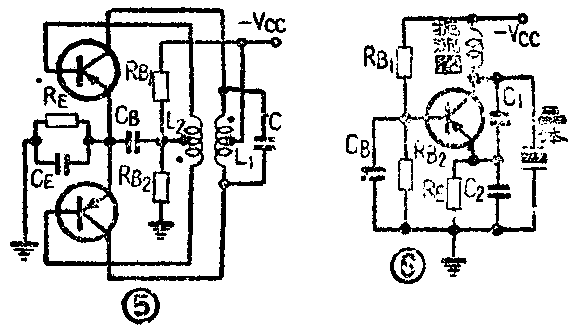
5.石英晶体控制的振荡器 为了得到更高的频率稳定度,在频率固定的振荡器中,常常采用石英晶体作为频率稳定元件,这种振荡器如图6所示。它在结构上与图3c的共基极晶体管振荡器相似。石英晶体在它的固有频率下等效于一个高Q值的LC谐振回路,并呈现感性电抗的性质。反馈回路由电容C\(_{1}\)和C2组成,它们的数值要取得大一些,使得振荡频率接近于石英晶体的固有频率。(李锦林)