RC电路

由电阻R和电容C组成的电路，简你RC电路。这是脉冲技术中最简单、最基本和应用最广的电路。这里想谈谈这种电路中的工作过程，即电路中电流和电压随时间的变化情况，并介绍脉冲技术中的一些基本概念。

无线电爱好者都知道用万用表来检验大容量电容器的方法。把万用表放在测电阻的一档。用两根试棒分别接到待测电容器的两端；这时，电表指针突然偏转到某一读数，之后又逐渐返回到起始点。于是我们断定电容器是完好的。

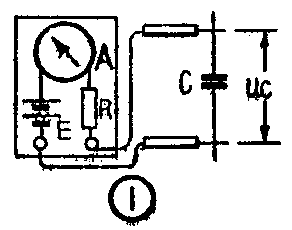
在检验电容器时，万用表实质上是像图1那样由电池E、电流表A和电阻R接成的串联电路。当这个电路和电容器C连接时，电池E就通过电流表A和电阻R向电容C充电，充电电流使指针偏转。以后，随着C上的电荷起来越多，C上的电压越来越高，充电电流逐渐减小。最后，C上的电压等于电池的电压，电路中就没有电流了。

从上例可以看出，当万用表没有接到C上时，C上的电压为0，这是一种稳定状态，简称稳态。当电表接到C上很久以后，C上的电压u\(_{c}\)等于电源电压E，电路中也没有电流流过，这又是一种稳定状态。但是，在万用表刚接到电容C上时，电路中的电流有一个突然增加和逐渐减小的过程，电容器上的电压也有一个逐渐增加到E的过程。这种从一个稳态转变到另一个稳态所经历的过程，叫做过渡过程，或称瞬变过程。与之对应的状态，称为过渡状态或瞬变状态，简称瞬态。在脉冲技术中，主要是研究瞬变过程。

研究瞬变过程时，有一个非常重要的概念，就是电容器上的电压，要从一个数值变到另一个数值，必须经过一定的时间。这时间一般很短，例如可达几微秒甚至更短，但总是需要一定时间的。换句话说，电容器上的电压不能跃变，只能随着时间逐渐地变化。这是因为电压的变化对应着电容器上电荷Q的变化，而电荷Q的积累和散去是要一定时间的。我们知道，电容器上电荷的增加，等于电路中的电流乘上时间。如果电流为i，那么在某一时间间隔△t内增加的电荷△Q就等于i乘△t即△Q=i×△t。从这个式子可以看到，不管实际的电流i是多么大，只要△t等于零，△Q就等于零。也就是说，电容器上的电荷Q不能跃变，因而电容器上的电压也就不能跃变。再从能量方面看，电容器中所储存的电能Wc=\(\frac{1}{2}\)Cu\(^{2}\)\(_{c}\)。而能量的变化△Wc=功率×△t。在实际电路中，不管电源功率有多大，只要△t=0，△Wc就等于0，也就是说能量不能跃变，因而与之相应的电容器上的电压也就不能跃变。

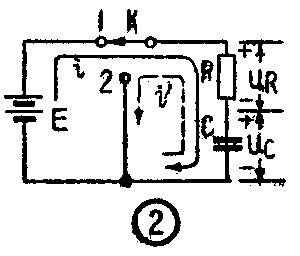
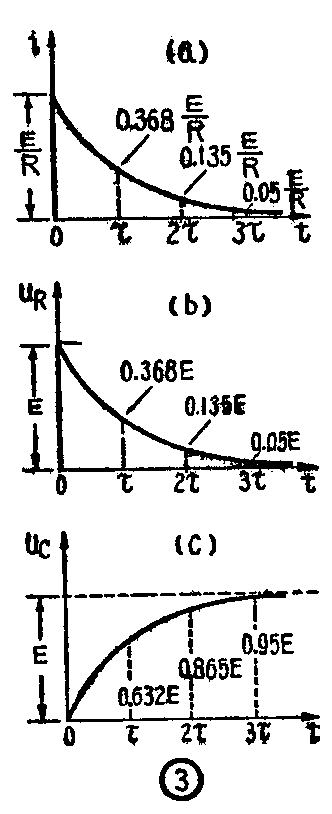
现在我们回过头来看看用万用表检验电容器的电路。这实际上就是一个RC电路。为了明显起见，我们把它改画成图2中的样子。在开关K未接到点1以前，电容器上没有电荷。u\(_{c}\)=0。当K刚一关闭的瞬间（t=0的瞬间），由于C上的电压不能跃变，uc仍等于0（图3c）。因而整个电源电压E都加在电阻R上，R上的电压跃变到E（图3b）。根据欧姆定律，R中的电流i也相应地跃变到\(\frac{E}{R}\)（图3a）。这个电流也就是电路中对电容C充电的电流。随着对电容C的充电，u\(_{c}\)逐渐增加，而uR=E-u\(_{c}\)逐渐减小，相应地，i=E-uc;R也逐渐减小。i、uR、u\(_{c}\)随时间的变化图形如图3所示。由此可见，当开关刚关闭时，充电电流最大，等于\(\frac{E}{R}\)而随着电容C的继续充电，充电电流却逐渐减小。

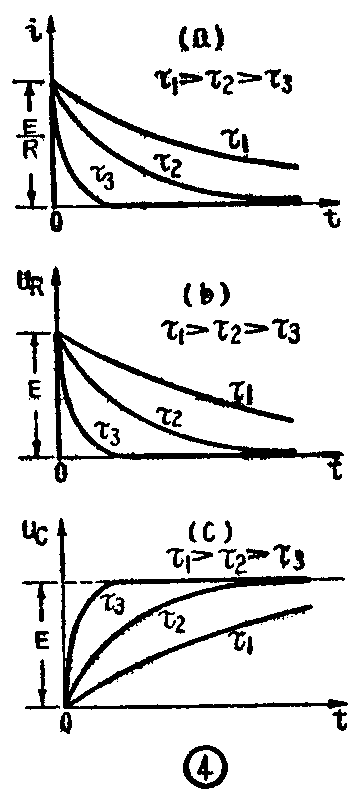
充电电流i和电阻上的电压降u\(_{R}\)的减小速度，以及uc的增加速度，决定RC的乘积。RC相乘得出的是一个代表时间的数值。因为R=\(\frac{电压}{电流}\)，C=电量;电压，所以RC=\(\frac{电压}{电流}\)×电量;电压=\(\frac{电量}{电流}\)=时间。如果R用欧，C用法，得出的时间单位就是秒。因此我们可以把RC的乘积叫做时间常数，通常以字母τ表示。τ＝RC越大,u\(_{c}\)的增长和iR、u\(_{R}\)的下降就越慢。因为R越大，充电电流就越小，uc的增加就越慢；C越大，它的电压增加就相应于更多的电荷积累，因而在同样的充电电流下，电压的增加就较慢。图4画出了不同τ值下的电流、电压随时间变化的曲线。由图可见，虽然都是相同的RC电路，但如果RC的乘积很大（例如等于τ\(_{1}\)），电流和电压的变化就很缓慢，如果RC的乘积很小（例如等于τ3），电流和电压的变化就很快。用万用表检验电容器时也有这样的体会，如果电容C很大，就可以看到指针跳到最大值后缓慢地回到起始点；C较小时，指针的回程就较快；如果C很小，指针还未来得及跳动时充电电流即已迅速减小，指针就根本不能动了。因此这种方法只能检验大容量电容器。

理论证明，充电电流i、电压u\(_{R}\)和电压uc随时间t的变化可用下列公式表示：

式中e\(^{-}\)\(\frac{t}{τ}\)是y=ex形式的指数函数，这里x=-t;τ是自变数，e≈2.72是自然对数的底。

从这些公式可以看到，当t=0时，e\(^{-}\)\(\frac{t}{τ}\)=eo=1, 因而i=E;R,u\(_{R}\)=E,uC=0。t=τ时，e\(^{-}\)\(\frac{t}{τ}\)=e-1=1;e=0.368,因而i=0.368\(\frac{E}{R}\),u\(_{R}\)=0.368E,uC=(1-0.368)E=0.632E（参看图3）。t=2τ时，e\(^{-}\)t;τ=e-2=\(\frac{1}{e}\)\(^{2}\)=0.135,因而i=0.135E;R,u\(_{R}\)=0.135E,uC=(1-0.135)E=0.865E。t=3τ时，e-\(\frac{t}{τ}\)=e\(^{-}\)3=1;e3=0.05, 因而i=0.05\(\frac{E}{R}\),u\(_{R}\)=0.05E,uC=(1-0.05)E=0.95E。…最后，只有当t=∞时，才能使e\(^{-}\)t;τ=e-∞=\(\frac{1}{e}\)\(^{∞}\)=0,从而使i=0,u\(_{R}\)=0,uC=E。

从理论上说，只有经过无限长的时间以后，才能达到新的稳态。但是，由于t=3τ时，电路中的状态即已和稳态很接近，所以实际上可以认为当t＞3τ时，电路已达到稳定状态。

设图2电路中电容器已充电到u\(_{C}\)=E。现在突然把K扳到2的位置，电容器将通过R放电。

上面讲过，电容器C上的电压不能跃变。当K刚扳到2的瞬间，C上的电压仍然是E，这个电压整个加到电阻R上，不过这时R的下端为正，上端为负，所以R上的电压为-E。电路中的放电电流i′=-ER，刚好和充电电流i的方向相反。随着电容器的放电，u\(_{C}\)逐渐减小，i′和uR也逐渐减小（见图5）。

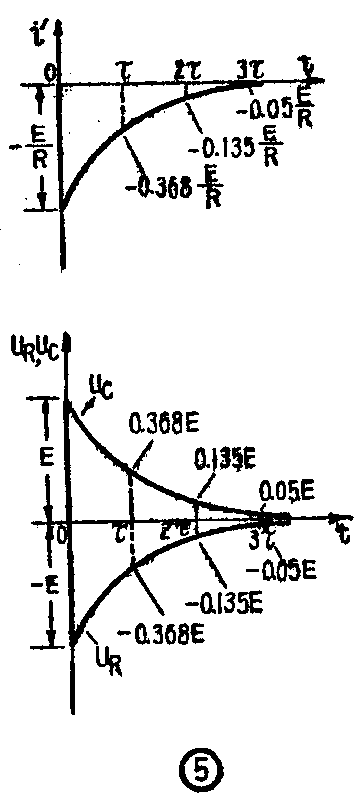
和充电时一样，当t=τ时，各电压电流减小到起始值的0.368；t=2τ时，减小到起始值的0.135；t=3τ时，减小到起始值的0.05，此后，即可以认为放电完毕，达到新的稳态。

由上述的情况可知，当电容器充放电时，电容器的电压和充放电电流从起始值变到某一给定数值所需的时间，决定于时间常数τ。因此可以利用具有不同时间常数的RC电路，做成具有各种延迟时间的继电器。

我们来看一下图6的电路。这时，加在RC电路两端的不是直流电源E，而是一连串矩形脉冲。而时间常数τ=RC甚小于脉冲持续时间ti。我们从R的两端取得输出信号。根据前面的分析可知，当脉冲到来时，输入端电压由0跃变到脉冲幅度电压U，R上的电压也相应地跃变到U。但是因为τ=RC远小于t\(_{i}\)，所以R上的电压随即下降到零，从而在输出端得到一个很短的尖头脉冲。这时，C上的电压等于输入电压U。当脉冲终止时，输入端的电压突降为0，等于输入端短路，C上的电压U整个加到电阻R上，使R上的电压从0跃变到-U。又因时间常数很小，C的放电电流随即减小到零，R上的电压也相应地变到零，从而在输入端得到一个负的尖头脉冲。由此可见，这种电路可以把输入的矩形波变成一连串短脉冲，正脉冲和矩形波的前沿相应，负脉冲和短形波的后沿相应。这种电路和为微分电路，它在脉冲技术中应用极广。RC微分电路的特点是，第一，从电阻R上取得输出电压；第二，电路时间常数τ=RC必须甚小于脉冲持续时间。

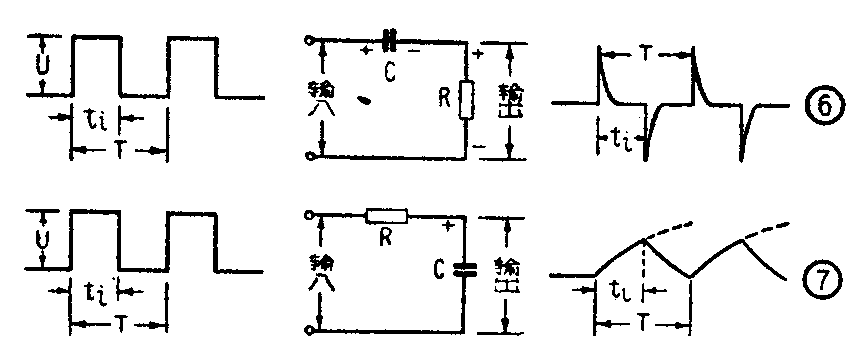
图7的电路和图6刚好相反。它是从电容器C上得到输出电压，同时，电路的时间常数τ=RC甚大于脉冲持续时间ti。这样，当矩形脉冲到来时，C上的电压将在整个脉冲持续时间内缓慢地增长。还未增长到U时，脉冲即已终止。脉冲终止后，电容器又通过电阻R缓慢放电，其上的电压、缓慢下降，结果就在电路的输出端得到了如图中所示的锯齿波。这种电路称为积分电路，它在脉冲技术中的应用也很广。RC积分电路的特点是，第一，从电容器C上取得输出电压；第二，电路时间常数τ=RC必须甚大于脉冲持续时间。（黎明）