交流电流是大小和方向都在不断变化的电流。其中最常见的是像附图那样按正弦规律变化的电流。这个曲线表明,在每一个确定的瞬间(例如t\(_{1}\)、t2、t\(_{3}\)),都对应着一个大小和方向都完全确定的电流值(i1、i\(_{2}\)、i3)。每一具体瞬间的实在电流值,就叫做瞬时值。
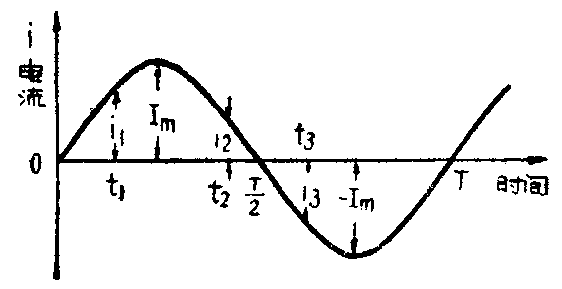
交流电流达到的最大值,如图中的I\(_{m}\)所示,叫做振幅值,或称幅度、幅值、峰值。
有效值又是什么呢?正如直流电流通过电阻R会发热一样,交流电流通过电阻R也会发热。现在把某一交流电流和某一直流电流分别通过相同的电阻R。如果在交流电流一个周期的时间内,两个电流在电阻R上所产生的热量相同,那么,从热效应这一角度来看,两个电流(交流和直流)是等效的。因此可以用这个直流电流的数值来表示交流电流实际产生的热效果,而这个数值就叫做交流电流的有效值,通常以I表示。
大家知道,某一瞬间的电流i在电阻R上消耗的功率为i\(^{2}\)R。因此计算有效值时,需要求出各个电流瞬时值的平方在一周期内的平均值。这个平均值就相当于有效值I的平方。再把它开平方,就得到了有效值I。因此有效值又称为均方根值。有效值I和振幅值I\(_{m}\)间的关系为
I=I\(_{m}\)/\(\sqrt{2}\)=0.707Im。
和交流电流一样,交流电压也有相应的瞬时值、振幅值和有效值,两者的意义和算法完全一样。
在这几种数值中,有效值用得最多。交流仪表的刻度,一般标的都是电流或电压的有效值。在书刊、手册、电路中,除特别注明的以外,一般所说的交流电压、电流的数值,都是指的有效值。(不日)