一个奇怪的单位——分贝

（方波）无线电爱好者常常会碰到分贝（简写成“db”）这个名词。这是一个用来表示声音或电信号在传输过程中功率增加（增益）或减少（损耗）的计算单位。它和我们通常使用的许多单位有着截然不同的性质。例如我们从红布和蓝布上各剪下一尺，那么这两段布都短了一尺，而剪下来的两块布长度也必然相等。但分贝却不是这样。当一个电路的功率损耗一分贝时，这电路的功率减少了多少呢？这却要看电路原来的功率有多大。如果原来是100毫瓦，那么降低一分贝就是减少了约20毫瓦。如果原来只是10毫瓦，那就只减少约2毫瓦。显然20毫瓦并不等于2毫瓦。但我们根本不考虑这个事实，只要它们都减少了20％，就认为它们的功率损失都是一分贝。

可见，分贝所表示的是两个功率的比值，不过，它不是直接表示这个比值，而是通过一种特殊方法——对数——来表示的。

什么是对数呢？这里简单说明一下。大家知道，10×10=10\(^{2}\)=100；10×1O×10=103＝1000，……。我们把10\(^{2}\)、103等叫做乘方，其中10叫做底数，10右上角的数字叫做指数，100、1000……等叫做真数。知道了底数和指数，就可以求出真数（如10\(^{2}\)=10×10=100）。反过来，如果知道了底数10和真数100，也可以求出相应的指数2。这个相应的指数2，就称为100以10为底的对数。我们以符号log（读作laoge）表示对数，把底数写在log的右下角，这样，102=100，10\(^{3}\)=1000，……就可以写成log\(_{1}\)0100=2，log101000=3……，也就是说，100以10为底的对数为2,1000以10为底的对数为3……。如果以文字代替数字，可以写出log\(_{b}\) A=N，即A以b为底的对数为N（用指数表示可写成bN=A）。通常应用的是以10为底的对数，所以把以10为底的对数叫做常用对数，并且把log10简写为log。任何数的零次方都等于1，即b\(^{0}\)=1，所以log1=0。此外，对数还有一些重要的特性，例如：log（A×B）=logA+logB；log（\(\frac{A}{B}\)）=logA-logB，此时若A＞B，log（A;B）=logA-logB=正值，若A＜B，log（

把两个功率的比值（\(\frac{P}{_{2}}\)P1）取常用对数，就是这两个功率相差的“贝尔”数（贝尔是外国人名的译音）。贝尔这个单位太大了，用起来不方便，所以实际上常取贝尔的十分之一作为单位，叫做“分贝”，就好像一米的十分之一叫做“分米”一样。写成公式，就是

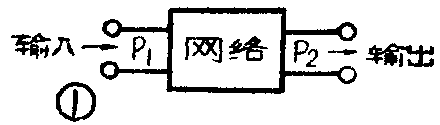
根据上述对数的性质可知，P\(_{2}\)＞P1时，\(\frac{P}{_{2}}\)P1＞1，分贝数就是正的；P\(_{2}\)＜P1时，P\(_{2}\);P1＜1，分贝数就是负的；P\(_{2}\)=P1时，\(\frac{P}{_{2}}\)P1=1，分贝数等于零。如果P\(_{1}\)是某一网络的输入功率，P2是该网络的输出功率（见图 1），那么P\(_{2}\)＞P1表示该网络使功率得到增益，所以正分贝数即代表功率增益；而P\(_{2}\)＜P1表示该网络使功率得到损耗，所以负分贝数即代表功率捐耗。P\(_{2}\)=P1，分贝数为零，表示网络中既无增益，也无捐耗，输入功率和输出功率相等。

封三列出了功率比和分贝数的对应值。例如，1分贝的增益（＋1分贝）相当于

分贝与耳朵的关系。为什么一定要用分贝这个单位呢？这首先要从我们的耳朵谈起。原来人耳对声音响度变化的感觉，并不和声音功率的变化成正比，而是和引起这些感觉的声音功率之比的对数成正比。用分贝作单位正好反映了耳朵的这种特性。这样，不管原来的声强是大是小，只要声音功率变化的分贝数相同，人耳感到的响度变化都是一样的。

再举一个例子，也可以说明采用分贝的好处。人耳所能听到的声音，从细微的蚊鸣到震耳的响雷，其功率竟相差一万亿倍，写成数字就是1,000,000,000,000倍（10\(^{12}\)倍）。要把雷声和蚊鸣之间的各种声音功率进行比较时，就经常会遇到几万万倍或几万万分之一等令人头痛的数字。但是当采用分贝表示时，雷声和蚊鸣之间，只不过是10log1012=120分贝之差。这对我们的记忆、书写和计算，当然要方便得多。

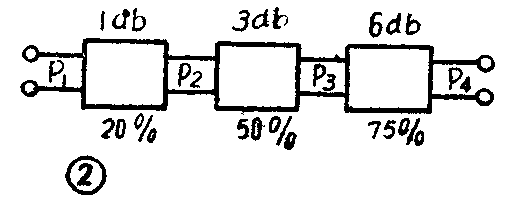
把乘除变成加减。假定有三个网络，它们分别引起20％、50％和75％的功率损失（图2）。如果输入端的功率P\(_{1}\)是100毫瓦，那么，经过第一个网络后，只剩了80％：

经过第二和第三个网络后的功率将分别是：

要得到输出功率P\(_{4}\)的结果，非得连续计算三次不可，如果这样的网络有很多个，它们的增益和损耗又各不相同，那么我们就得整天泡在这种麻烦的连乘连除中了。这时，分贝就来帮忙了。把每个网络的增益或损耗写成分贝数，那么第一个网络损耗分贝数为10logP2P\(_{1}\)，第二个为10logP3;P\(_{2}\)，第三个为10logP4P\(_{3}\)。根据前述对数的性质，总的分贝数为10logP4;P\(_{1}\)=10log（P2P\(_{1}\)·P3;P\(_{2}\)·P4P\(_{3}\)）=10logP2;P\(_{1}\)+10logP3P\(_{2}\)+10logP4;P\(_{3}\)，即总的分贝数为各个网络的分贝数之和，在上述例子中即为1db＋3db＋6db＝10db，而100毫瓦的功率经过10db的损耗后正好得到10毫瓦这个结果（建议读者利用封三数据自行验算证明）。这就是说，只要把增益和损耗化成分贝数进行加减就可以了。很明显加法比乘法计算简便得多。

如果一个放大器有10db的增益，那就表示它在正常的情况下，可以把输入电功率的水平提高到十倍。我们常把这种表示两个功率比的公贝数称为相对功率电平或相对电平。前面所谈的，都是相对电平的分贝数。但是，放大器增益的相对电平值只能说明输出功率和输入功率的相对关系，如果不告诉我们输入功率的大小，则仍然无法知道输出功率的实际数值。

仿照以海平面为参考点计算山高的方法，也给电功率规定了一个比较标准。常用的比较标准是一毫瓦（也有采用六毫瓦等标准的）。每一功率和这种标准比较后，便可得到一个相应的分贝数（符号为db\(_{m}\)）。 在这种情况下，每一个分贝数都表明一个实际的功率。因此我们把这种表示电路某点功率水平的分贝数称为绝对电平。写成式子，就是

由绝对电平的定义可知，某一功率P\(_{x}\)大于1毫瓦时，它的绝对电平分贝数就是正的；当Px小于1毫瓦时，绝对电平分贝数就是负的，P\(_{x}\)=1毫瓦时，绝对电平就是0分贝。

要计算某一绝对电平分贝数所对应的实际功率，可以利用封三的分贝表，只需把各个功率比乘上1毫瓦就行了。例如，电路中某点的绝对电平是+3db，那么，从表中查得功率比为1.995，这点的实际功率就是1.995×1毫瓦=1.995毫瓦。

功率P和电压U、电流I以及电阻R之间有下列关系：

因此，电路某两点间的相对电平分贝数

如果这两个电阻相等（R\(_{1}\)=R2），那么

由此可见，在电路两点处的电阻相同时（或者在电路的同一点上），可以通过电流比或电压比求得相对电平的分贝数。从封三的分贝表中，可以找出和某一分贝数相应的电压比或电流比。如果R\(_{1}\)不等于R2，就不能用式（5）或分贝表直接根据电压比（或电流比）求得分贝数。这时必须知道R\(_{1}\)和R2的实际数值，利用公式（4），也就是按照功率比来求分贝数。

和前面规定出功率的绝对电平一样，也可以规定出绝对电压电平或电流电平的分贝数。但是由于两个相同的电压（或电流）在不同电阻上所得到的功率是不同的，所以规定零电压（或电流）电平时，必须同时指出这个电平是在什么电阻上得到的，也就是规定出标准电阻。通常以在600欧电阻上得到1毫瓦功率的电压（或电流）作为零电压电平，即

零电压电平

零电流电平

如果在电路中阻抗为600欧的某点上，测得电压为U\(_{x}\)伏、或电流为Ix毫安，则该点的

要求某一绝对电压（或电流）电平的分贝数所对应的实际电压（或电流），可以利用封三的分贝表，只需把各个电压比（或电流比）乘以0.775伏（或1.29毫安）就行了。

如果电路中的阻抗不是60O欧，那么就不能用式（8）和（9）来求绝对电平，这时最好是把电压或电流变为功率来求绝对电平。

在数学中，除了上面所说的常用对数外，还有一种以e（e=2.718……）为底的自然对数（这种对数的符号为loge，简写为ln）。如果把功率比取自然对数，再乘以1/2，就是相对电平的奈倍数。写成式子，就是

如果以1毫瓦的功率作为零电平，则

和分贝的情况一样，在电路某两点的电阻相同（R\(_{1}\)=R2）时，也可以根据电压比或电流比来求得奈培数：

奈培的性质和分贝一样，它们都是用来表示功率增益（或损耗）的大小和电平高低的，就好像米和尺都是用来表示长度一样。我们知道，米比尺长，1米=3尺，相似地，奈培比分贝大：