谐振

各种不同频率的无线电台所发出的无线电波，当它们接触到收音机的天线时，都会在天线中感应出交变电流。因此，收音机必须具有挑选电台的能力，否则，扬声器或耳机里将同时发出所有电台的播音，混在一起，结果什么也听不清楚。用甚么办法来挑选电台呢？原来收音机中有许多由电感线圈和电容器所组成的振荡回路，这些振荡回路具有一个奇妙的特性——谐振，收音机就是利用振荡回路的谐振特性来选择电台的。在这篇文章里，我们就来简单谈谈有关谐振的一些知识。

如果把一个简单的摆（见图1）从它的静止位置O移到A点，然后一松手，摆就会来回摆动。由于这种摆动是在没有外力的作用下进行的，因此叫自由振荡。它的频率就等于摆的固有频率。但是如果我们一直用手周期性地推动摆，那么摆就不能“自由”地摆动，而只能随着外加的推动力来摆动。这时摆的振荡频率就决定于手的推动频率：我们每分钟推动十次，摆就每分钟摆动十次。摆在外力的作用（手的推动）下进行的摆动，就叫作强迫振荡。十分明显、强迫振荡和自由振荡是不同的，强迫振荡的频率和固有频率无关，而完全决定于外力的频率。

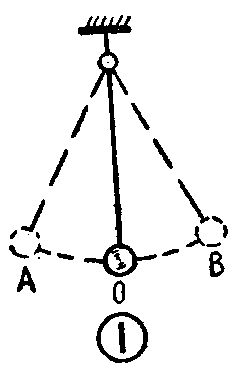
强迫振荡的幅度不但决定于外力的大小，而且和外力的频率有很大的关系。在外力大小不变的情况下，当它的频率和摆的固有频率相同时，所引起的强迫振荡幅度最大。反之，当频率不相同时，所引起的强迫振荡就很小。外力的频率和固有频率相同时，强迫振荡幅度最大这一现象就叫作谐振。

谐振是一种很常见的现象。例如，我们把发声频率相同的两个音叉并排地放在一起。敲击其中的一个音叉时，周围的空气就会随着音叉的振动频率而振动，这振动的力量虽然很小，但是由于它的频率和另一音叉的固有频率相同，所以能使另一音叉振动发出声音来。又如我们在荡秋千时，也可以体会到，只有当两脚用力得当，和秋千的固有频率“合拍”时，秋千才会越荡越高。

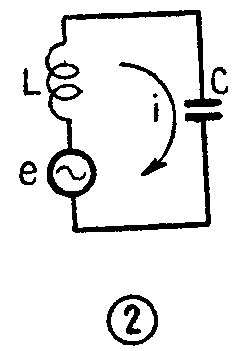
如果我们在LC振荡回路里串接了一个频率力f的交流电源e（图2），那么，回路里就只能有频率为f的交流电流i流过。也就是说，回路中发生了强迫振荡。这个振荡的频率等于外加电源的频率f，而不等于回路的固有频率f\(_{0}\)。和机械振荡时相似，当外加交流电源的频率f=f0时，流过回路的电流i最大而发生了谐振。

振荡电路的谐振有两种情况，一种是串联谐振，一种是并联谐振。下面我们分别来谈谈这两种情况。

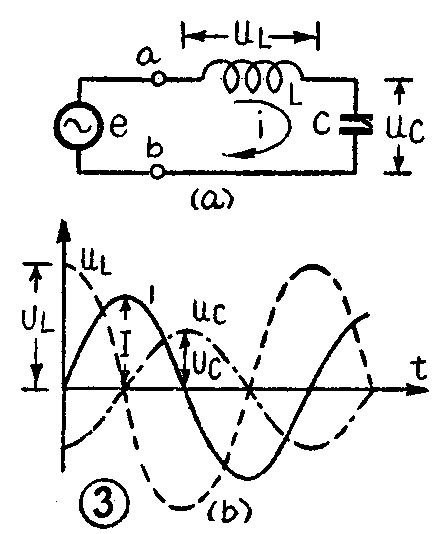
在图2的电路中，电感L、电容器C和外加交流电源e是相串联的。在这种串联电路中产生的谐振，就叫做串联谐振。为了便于分析，我们把图2的电路改画为图3a的形式。这时流过L和C的电流是同一个电流i，但是L和C两端的电压u\(_{L}\)和uC可并不一样。U\(_{L}\)比i超前90℃，如图3b中虚线所示；而uC则比i落后90℃，如图中点判线所示（参考本期谈相位一文）。这样，u\(_{C}\)和uL的变化正好是相反的。u\(_{L}\)为正时，uC正好为负。因此，这两个电压在电路中是互相抵消的。

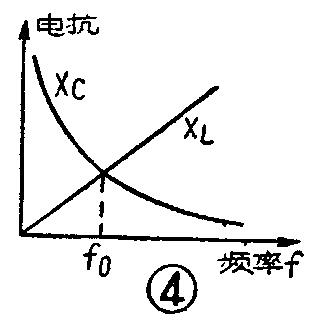
我们知道，电容器两端的电压U\(_{C}\)=XCI（在这里和以后都用大写字母U、I等代表电压、电流的幅度值），其中X\(_{C}\)=\(\frac{1}{2πfC}\),是电容器的电抗。频率f越高，XC越小(参看图4)。电感线圈两端的电压U\(_{L}\)=XLI，其中X\(_{L}\)=2πfL，是电感线圈的电抗，f愈高，XL愈大。从图4可以清楚地看到，在某一频率f\(_{0}\)时，XC=X\(_{L}\)，因而UC=U\(_{L}\)，也就是说uC和u\(_{L}\)大小相等，方向相反，它们在电路中就完全抵消了。这时ab两点间的总电压uab等于零，这说明ab两点间对电流i毫无阻抗（阻抗Z=U\(_{ab}\);I=0I=0），因此电流i达到极大的幅度（在回路中没有电阻的理想情况下，可以达到无穷大），这就是发生了谐振。谐振时，XC=X\(_{L}\)，

可见这个谐振频率正好等于振荡回路的固有频率。

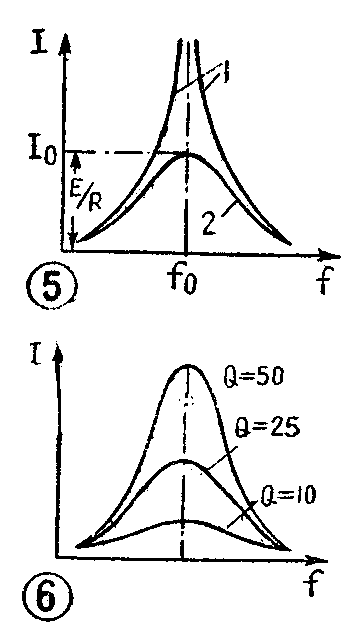
当外加电源频率f小于f\(_{0}\)时，由图4可见，XC大于X\(_{L}\)，uC大于u\(_{L}\)。这样，uC抵消了u\(_{L}\)以后还有余，ab两点间的总电压等于（uC-u\(_{L}\)），和uC同方向，而整个振荡回路表现为容抗（X\(_{C}\)-XL）。f和f\(_{0}\)相差越大，（XC-X\(_{L}\)）就越大，所以回路中的电流就越小。与此相似，当外加电源频率f大于f0时，X\(_{L}\)大于XC，u\(_{L}\)大于uC，ab两点间的总电压等于（u\(_{L}\)-uC），整个振荡回路表现为感抗（X\(_{L}\)-XC）。f比f\(_{0}\)大得越多，（XL-X\(_{C}\)）就越大，回路中的电流就越小。由此可以得到回路电流的幅度I随外加电压频率f而变化的曲线，如图5中曲线1所示。这个曲线称为谐振曲线。

在实际的振荡回路中，总有一定的电阻R（如线圈本身的欧姆电阻，电容器的损耗电阻等），因此在发生谐振时，虽然容抗X\(_{C}\)和感抗XL相互抵消，但回路总阻抗仍然不等于零，而是等于R；回路谐振跑流的幅度I\(_{0}\)不能达到无穷大，而是等于E/R。因此实际振荡回路的谐振曲线如图5中的曲线2所示。

振荡回路可以用它谐振时的感抗2πf\(_{0}\)L（或容抗\(\frac{1}{2πf}\)0C对电阻R的比值来说明它的特性。这个比值叫作振荡回路的品质因数或Q值；

R越大，Q值就越小。在良好的振荡回路中，Q值大于100。

Q对回路的谐振特性有很大的影响。回路的Q值越大，它的谐振曲线的形状就越尖锐越高，如图6所示。

串联谐振时，由于回路中的电流I\(_{0}\)很大，因此L和C两端间的电压UL和U\(_{C}\)也很大：

从这里可以看到，串联谐振时L和C两端的电压是外加电压的Q倍。因此在Q值很高的情况下，它们就会大大超过外加电压，仿佛回路把电压“放大”了似的。由于串联谐振具有这样的特点，所以又叫作电压谐振。

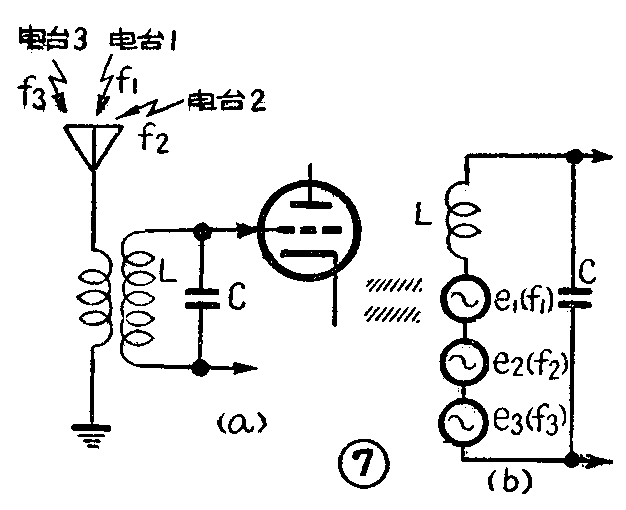
利用串联谐振现象可以选择电台。图7a是大家所熟悉的收音机输入电路。每个电台发出的无线电波接触到天线时，都在天线回路中产生一个高频交变电流，这个电流流过输入变压器的初级线圈，在次级线圈里感应出一个高频电压。这样，图中所示的不同频率的三个电台分别在次级回路中产生频率为f\(_{1}\)、f2和f\(_{3}\)的高频电压e1，e\(_{2}\)和e3（图7b）。但是只有当电压的频率f和f\(_{0}\)相同时才会在回路中产生很大的电流。因此，只要改变回路的L和C，使回路的固有频率f0=1／2π\(\sqrt{LC}\)等于我们所要听的电台的频率，比如说f\(_{1}\)，那么这时e1就会在回路中产生很大的电流，而电子管的栅极上就得到一个大小为QE、频率为f\(_{1}\)的高频电压（就是回路电容C两端的电压）。与此同时，由于f2、f\(_{3}\)不等于f0，e\(_{2}\)、e3在回路中产生的电流很小，电子管栅极上频率为f\(_{2}\)、f3的高频电压也就很小。这样，利用串联谐振的这种特性，回路就把电台1挑选出来，收音机的扬声器里就只能发出电台1的播音。

调节回路的L或C，使回路和外来信号发生谐振的这一步骤，就是大家所熟悉的所谓“调谐”。

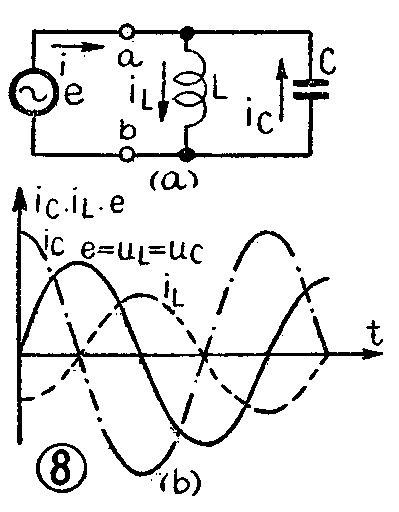
并联谐振回路如图8a中所示。这里，外加电源e是和L、C并联。

由图中可见，这时L和C两端的电压是相同的，u\(_{L}\)=uC=e，不过流过L和C的电流并不一样。我们知道，流过L的电流i\(_{L}\)在相位上比e落后90°，如图8b中虚线所示。流过C的电流iC在相位上比e超前90°，如同一图中点划线所示。从这里我们可以清楚地看到，不论在任何一个时刻，i\(_{L}\)和iC的方向总是相反的。如果i\(_{L}\)是正的，由a端流向b端，那么iC就是负的，由b端流向a端，而流入回路的总电流i是i\(_{L}\)和iC的和。由于i\(_{L}\)和iC的方向恰好相反，因此它们在电路中有相互抵消的趋势。

当外加电源的频率f等于固有频率f\(_{0}\)=\(\frac{1}{2π}\)\(\sqrt{LC}\)时，就发生并联谐振，这时由于f=f0时，X\(_{L}\)=XC，因此I\(_{L}\)=E;XL和I\(_{C}\)=\(\frac{E}{X}\)C相等，也就是说，i\(_{L}\)和iC大小相等，方向相反，它们就完全相互抵消了。这样一来，尽管ab两端间加着一个交流电源e，但是流过ab的总电流i却等于零。这说明f=f\(_{0}\)时，ab两端间的回路阻抗ZK等于无穷大。在其他的频率时，由于XL和X\(_{C}\)不相等，iC和i\(_{L}\)不能完全抵消，i不等于零，而回路阻抗是比较小的。当f小于f0时，X\(_{L}\)比XC小，因而i\(_{L}\)比iC大，这样i\(_{L}\)抵消了iC后还有余，总电流i和i\(_{L}\)同方向而落后于e90°，因此这时的回路阻抗是个感抗。而且f越小，这个感抗就越小，总电流i就越大。与此相反，当f大于f0时，X\(_{C}\)比XL小，因而i\(_{C}\)比iL大，i\(_{C}\)抵消了全部iL后还有余。总电流i和i\(_{C}\)同方向而超前于e90°，这时的回路阻抗是个容抗。而且f越大，这个容抗就越小，总电流i就越大。

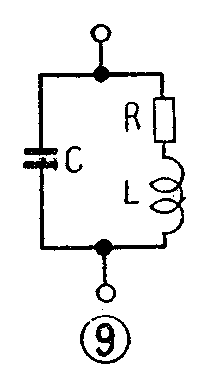
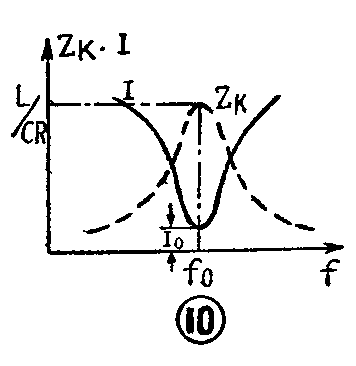
上面所谈的是理想情况。实际上由于回路里总有一定的电阻R（如图9），要消耗一定的能量，因此并联谐振时的回路阻抗并不等于无穷大，而不过是一个相当大的电阻。通过计算可以求得这个电阻值等于L／CR。同时，谐振时的总电流不是等于零，而是等于E/\(\frac{L}{CR}\)=I\(_{0}\)。考虑了R以后，回路阻抗ZK、总电流I和f的关系如图10中的曲线所示，这条曲线就是并联谐振曲线。

并联谐振回路同样用Q值来说明它的特性。和串联谐振回路一样，Q值是谐振时的感抗（或容抗）和电阻R的比值，即

这就是说，谐振时i\(_{C}\)和iL是i\(_{0}\)的Q倍，因此如果回路的Q值很高，iC和i\(_{L}\)就会比i0大得多。由于并联谐振具有这样的特点，因此它又叫作电流谐振。

从上面的介绍中，我们看到并联谐振和串联谐振之间有相同的地方，也有不同的地方，为了更好地了解它们，在表1中对它们作了一个比较。

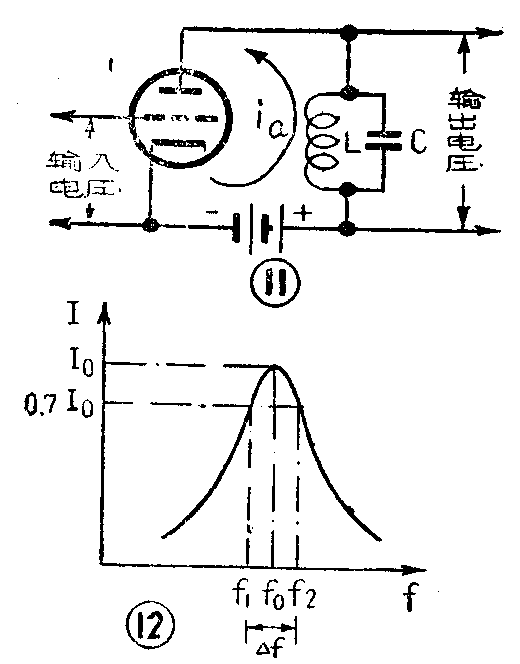
尽管并联谐振和串联谐振时的特性不一样，但同样可以用来选择电台。收音机里的高频放大器（如图11中所示）正是以并联谐振回路的谐振特性为基础的。在高频放大器中，接在电子管屏极电路中的谐振回路是和交流电源（电子管）并联的。放大器的栅极上加着要放大的交变电压，放大了的输出电压则从并联谐振回路两端取得，其大小为I\(_{a}\)ZK。由于高频放大器中一般采用五极管，内阻R\(_{i}\)很大，要比ZK大得多，所以屏流i\(_{a}\)的大小主要决定于电子管的内阻Ri，而基本上和Z\(_{K}\)的大小没有关系。因此，ZK越大时，输出电压就越大。这样一来，如果我们要从输入电压中挑选出频率为f\(_{1}\)的信号，就可以改变回路的L或C，使它的固有频率f0等于f\(_{1}\)。这时，对于频率为f1的信号，回路就发生并联谐振，回路阻抗Z\(_{K}\)最大，因而输出电压很大。对于输入端其他频率的信号来说，ZK要比谐振时小得多，因而输出电压就很小。这样，就把频率为f\(_{1}\)的信号挑选出来了。

从上面的介绍中可以知道，由于回路的谐振特性，无论对串联谐振回路也好，对并联谐振回路也好，只有频率在f\(_{0}\)两侧的一个频带内的信号，才能被回路挑出来而能良好地通过，这个频带就叫做回路的通频带。通频带一般是以回路电流I（或回路电压）减小到谐振值I0的0.7倍为标准的。例如图12中由f\(_{1}\)到f2之间的频带就是回路的通频带。

通频带说明了回路选择性的好坏。它的宽度△f和谐振曲线的形状有很大关系。如果回路的Q值越高，谐振曲线就越尖锐，通频带就越窄，回路选择电台的能力就越强。通过计算可以证明：通频带的宽度△f和f\(_{0}\)、Q之间有一个简单的关系：

这就是说，回路的Q越高，通频带就越窄。（莫愁）