作为一个无线电爱好者,你也许发生过这样的疑问:“为甚么通用的电阻器和电容器的电阻值和电容量都是一些‘奇怪的’数值呢?不是‘220’欧、‘470’千欧、‘8.2’兆欧……,就是‘110’微微法、‘4700’微微法…… 呢?”
原来,现代无线电工业生产的通用电阻器和电容器大都采用了一个如附表所示的标准化了的标称值系列。我们在实际上遇到的电阻器和电容器的数值,就是由附表中的基本系列的数值乘以1、10、100、1000……组成的。
E24(±5%) E12(±10%) E6(±20%)
系列值 系列值 系列值
1 1.0 1.0
1.1
1.2 1.2
1.3
1.5 1.5
1.6 1.5
1.8 1.8
2.0
2.2 2.2
2.4
2.7 2.7
3.0
3.3 3.3
3.6
3.9 3.9 3.3
4.3
4.7 4.7
5.1
5.6 5.6 4.7
6.2
6.8
7.5 6.8
8.2
9.1 8.2 6.8
E24采列是用x=24\(\sqrt{1}\)0\(^{n}\)的公式令n=1、2、3……计算而得来的。E12是由x=1210n得来的。E6是由x=6\(\sqrt{1}\)0\(^{n}\)得来的(在计算中实际上作了一定的修正)。这三个系列分别适用于误差在±5%、±10%、±20%以内的元件。
这些系列的特点是,系列中某一个数值的正误差极限正好和下一个数值的负误差极限基本上衔接起来(实际上可能略有重叠或间隙)。例如,在E24系列中,数值2.0的负误差极限1.9[由2.0-(2.0×5%)得来],与上一个数值1.8的正误差极限1.89[由1.8+(1.8×5%)得来]正好基本上衔接;2.0的正误差极限2:1[即2.0+(2.0×5%)]则正好与下一个数值2.2的负误差极限9.1[即2.2- (2.2×5%)]相衔接。
为什么要采用这样的系列值作为电阻器和电容器的标称值呢?
你一定同意这个事实: 不论多么高明的能工巧匠,都做不出两个或更多个绝对一模一样、丝毫没有差别的产品。在工业生产上,按照某种一定的规格生产大量产品时,所有的成品总是会发生或多或少离开规格的误差。无线电元件的生产也避免不了这种情形。
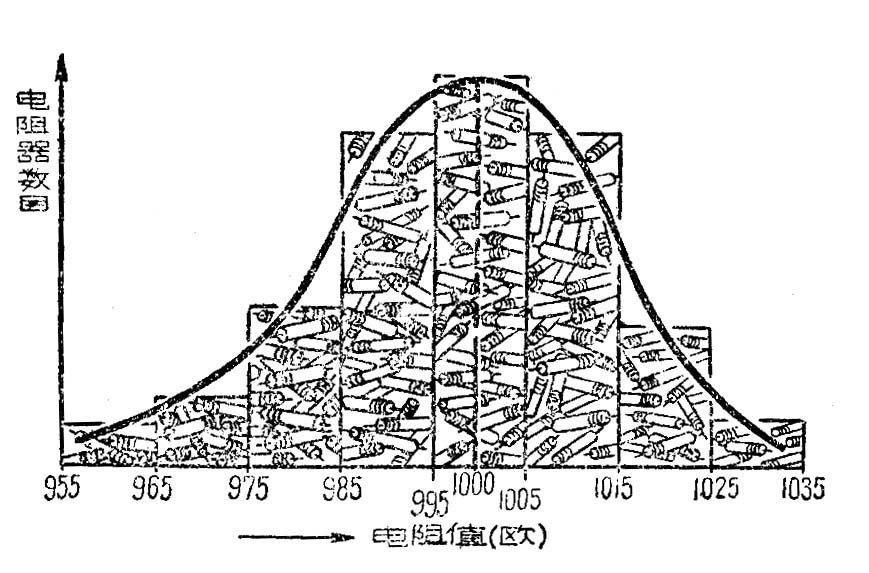
譬如,在生产一大批预定电阻值为1000欧的电阻器时,实际制成的产品总不可能都绝对准确地是1000欧。如果我们按照每相差10欧为一祖,把产品分选成为许多组,就会发现实际电阻值是按某种规律分布在1000欧的上下,正像图中所示那样。从图中可看出,数值接近于1000欧的产品较多,与1000欧相差愈大的产品愈少,这种规律性可以用图中的曲线来表示。在数学上,这一条钟形的曲线叫做“高斯曲线”或者“正态分布曲线”,它相当普遍地反映了生产中误差分布的规律。
因此,在生产中我们必须容许产品的实际数值和标称值有一定的误差,例如与标称值偏离±5%、±10;±20%等。并且,根据规定的误差和产品误差的分布规律,经过数学计算,得到附表的标称值系列。这样的系列,由于各个标称值的误差极限是互相衔接的,所以不论生产出来的零件误差大小,我们总是可以按照某一系列(E24、E12或E6)把它们归入某一标称值之下,换句话说,除非元件本身的结构和特性存在缺陷而成为废品以外,所有生产出来的元件,不论它本身的实际数值是多少,都可以按照一定标称值和误差等级分选出来,供给使用。这对于简化规格,降低生产成本,有很大作用。
反之,如果根据我们平时的习惯,选用1.0、1.5、2.0、2.5……9.5、10这样的系列,那么,在生产中按照这个系列和一定误差分选元件时,可能有许多元件既可以归入某一个标称值,又可以归入相邻的另一个标称值;也可能有某些元件无法归入任意一个标称值而成为不是废品的“废品”。例如规定误差为±5%,那么实际数值在1.05(即1+1×0.05)和1.425(即1.5-l.5×0.05)之间的产品,就既不能标1.0,也不能标1.5,因此便无法分选,变成“废品”了。
当你了解了上述标准化的标称值系列以后,就会知道,在实际选用元件时,应当考虑到实际应用中容许误差的大小,从这些系列中选出标称值和所需值最接近的元件来使用,而不会提出“我需要一个‘51微微法±20%’的陶瓷电容器”之类无法满足的要求。此外,当你需要譬如“68千欧±5%”的电阻器时,你最好不要期望到标有“68千欧±10%”或“68千欧±20%”标志的电阻器中去挑选一个具有±5%以内误差的(你也许早注意到了,误差愈小的元件价格愈贵吧?)。这常常会让你失望的。在大量生产元件时,一般总是首先按误差小的系列分选出一批元件以后,再把挑剩下来的元件按误差大的系列来分选;也可能是先按误差大的系列分选,然后从中再挑选出一批误差更小的元件,剩下的才作为误差大的元件出厂。(季才)