1.电子管的基本特性
大家知道,二极管是不能用来放大的。具有放大作用的最简单的电子管是三极管。三极管中有三个电极:阴极、屏极和在上述二电极之间的网状的控制栅极(简称栅极)。阴极不断地发射出大量带电的电子。视屏极和栅极所加电压的大小,这些电子中将有或多或少的部分能够穿过栅极飞到带正电的屏极上,构成电子管的屏流。
栅极电压对电子管屏流有很大的影响。如果栅极上加着正电压,那么它就帮助电子向屏极运动,使更多的电子到达屏极,结果屏流很大(见图1a)。当然,这时也有些电子会被栅极吸收构成栅流。但是如果栅压不是太大的话,这部分栅流是很小的。假如想象电子有足球那样大,那么按照同样的比例来说,栅极线匝间的距离便相当于宇宙中行星之间的距离。因而只有在飞向屏极的途中直接碰着栅极线匝或离线匝极近的少数电子,才能被栅极吸引构成栅流。相反,如果栅极加着负电压,那么栅极就拒斥电子,不让电子通过,因此屏流就小了(见图1b)。而栅极电压愈负,对电子的拒斥力就愈大,屏流就愈小。甚至可能使屏流截止。由此可见,电子管的屏流受栅极电压控制,随栅压的大小而变。
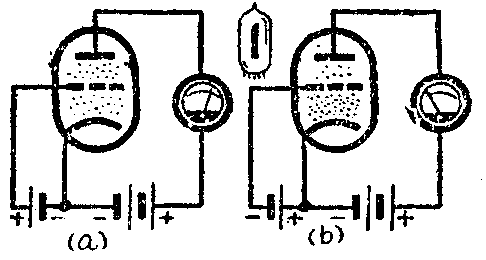
屏极电压对屏流也有一定的影响:屏压高,它对带负电的电子的吸引力大,跑到屏极上的电子就多了,因此屏流就大一些。反之,如果屏压低,屏流就小一些。然而由于屏极离开阴极要比栅极离开阴极远得多,所以它对屏流的影响远远没有栅压对屏流的影响大。
利用图2a的电路,可以得到当屏极电压U\(_{a}\)为某一定值时,屏流和栅压之间的关系如图2b所示。这条曲线叫做电子管的屏栅静态特性曲线,其中横坐标代表栅压,单位是伏;纵坐标代表屏流,单位为毫安。从图中可以清楚地看出,改变电子管的栅压可以控制它的屏流。使Ua保持另一定值,就会得到另一条静态特性曲线。对于不同U\(_{a}\)所得到的各个特性曲线构成了图2c中所示的静态特性曲线族。Ua愈大,在更负的栅压时也能得到相同的屏流,所以相应的曲线愈靠左。
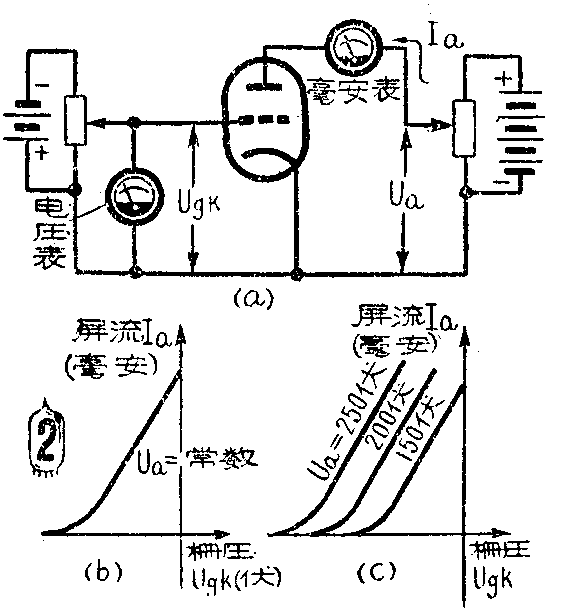
2.放大作用原理
为了大家容易明了起见,我们先来看看图3a所画的电路。在这个电路中,电子管的屏极直接接到电源上,因此屏极电压恒等于E\(_{a}\),在栅极上除了加上一个固定的负偏压Eg以外,还加有一个不大的交变信号电压U\(_{g~}\),这时电子管栅极上的总电压Ugk随着交变电压U\(_{g~}\)改变,而且在任何时刻都是负的(见图3b的下部)。
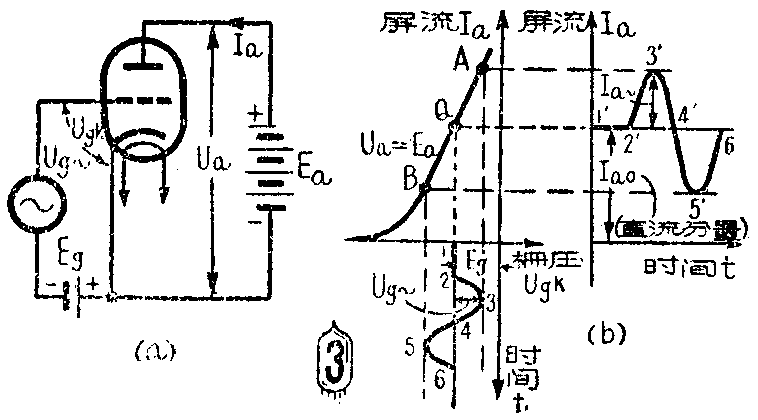
由于屏压U\(_{a}\)恒等于Ea,所以栅压和屏流就一定满足U\(_{a}\)=Ea的那条 静态特性曲线,因此利用这条曲线就可以确定栅极电压变化时屏流是怎样变化的。在图3b的横坐标下面画着不同的时刻t的栅极电压,纵坐标右面是相应的屏流变化。由图中可以看出,没有加上交变电压时,栅极电压就等于栅偏压(图中的1、2部分),而屏流也是一个常数,等于I\(_{ao}\)(图中的1'2'部份),Iao叫做静止电流。加上交变分量U\(_{g~}\)以后,栅压开始变化,屏流跟着发生改变,在栅极交变电压的正半周,屏流增加(因为这时栅极对电子的拒斥作用减弱),在负半周,屏流减小(因为栅极对电子的拒斥作用增强)。只要特性曲线的AB部份接近于直线,那么屏流的变化就和栅压的变化成正比。这样在栅极上交变电压的作用下,屏流中除了直流分量Iao以外,又出现形伏和输入信号电压U\(_{g~}\)相同的交变分量Ua~。
上述现象使我们想到,既然栅极上不大的交变电压能够在屏极电路中引起显著的交变电流,那么在屏极电路中接一个适当的负载电阻,使交变电流在这个电阻上产生很大的电压降,不就可以得到放大了的电压吗?确实如此;一个最简单的,也是最基本的电子管放大器就像图4a中所画的那样,其中R\(_{a}\)就是负载电阻,C是隔直流电容,它用以防止屏板上的直流电压也加到输出端上。
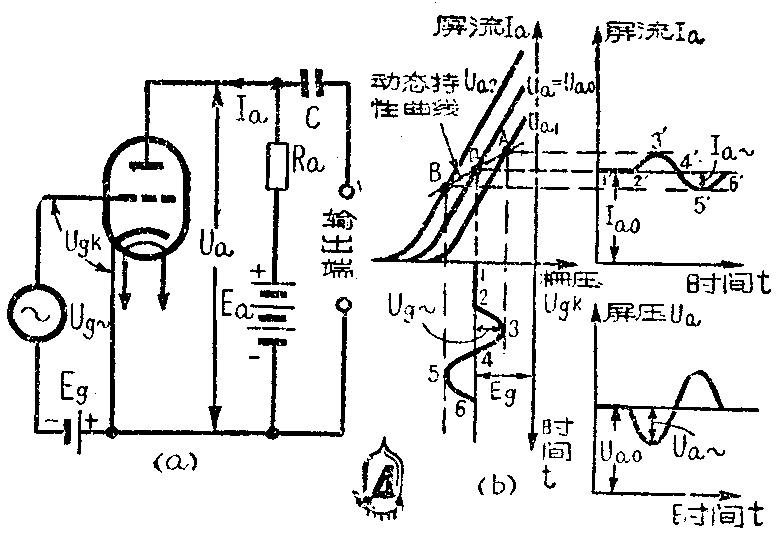
下面我们来看看图4a所示的最基本的放大电路中所发生的过程。在表面上看来,它不过只比上面所讨论的电路多了一个负载电阻R\(_{a}\),但是实际上这个电路却要复杂得多。在图3a,由于屏极直接接电源,因此无论屏流怎样改变,屏压是不变的。然而在现在的电路中,屏压Ua=E\(_{a}\)-IaR\(_{a}\),屏流的任何变化都会使屏压改变:屏流增大,屏压就降低;屏流减小,屏压就升高。这样,在栅极电压变化的同时,电子管的屏压也将发生变化,而这就使我们不能像以前那样用某一条静态特性曲线来确定由栅极电压的变化所引起的屏流变化是怎样的。例如,栅极上没有加交变电压时,屏极电压为Uao,那么这时屏流和栅压应该满足U\(_{a}\)=Uao的那条特性曲线(Q点),如图4b所示。在交变电压的正最大值时,由于屏流增加,在电阻R上的电压降增加,所以屏压降低为U\(_{a1}\),因而这时的屏流就不应在Ua= U\(_{ao}\)的曲线上确定,而应在Ua=U\(_{a1}\)的特性曲线上确定(图4b中的A点)。由此可见,栅压为不同值时的Ia应在不同的U\(_{a}\)的静态特性曲线上去找。这样我们可以得到一条通过Q点和A点的曲线BQA,这条曲线表示电子管屏极电路中接有负载电阻Ra时,屏流和栅压之间的关系,叫做电子管的屏栅动态特性曲线。它和R\(_{a}\)的大小有关,Ra越大,它的斜率越小,越靠近横轴,如图5所示。
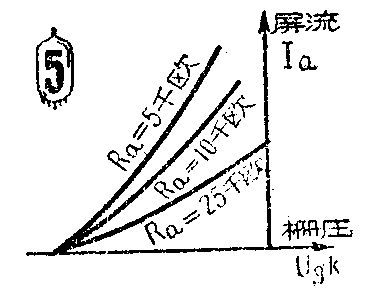
利用动态特性曲线就不难确定图4a的电路中栅压改变时,屏流是如何变化的。由图4b可以看出,在栅极交变电压的正半周,屏流增大;负半周,屏流减小。这个脉动的屏流流经负载电阻R\(_{a}\),在Ra上产生了脉动的电压降U\(_{R}\)=IaR\(_{a}\),因此屏极上的电压也是脉动的,包含一个直流分量Uao和一个交变分量U\(_{a~}\)。而Ua~通过电容C加到输出端上作为输出电压。这样,只要把R\(_{a}\)选得足够大,在图4a的输出端就可以得到一个比输人电压Ug~大得多的交变电压U\(_{a~}\)。
输出电压和输入电压的比值K叫做放大器的放大系数:
K=\(\frac{输出电压}{输入电压}\)=U\(_{a~}\);Ug~,
它说明输出电压为输入电压的多少倍。一般地说, R\(_{a}\)愈大,放大系数就愈大。
3 电子管的交流等效电路,R\(_{a}\)对放大系数的影响
一开始我们就谈到,屏压对屏流也有一定的影响。当栅压保持不变时,屏压越高,屏流就越大。因此如果屏压变化的话,屏流随着改变,而且屏流的变化量和屏压的变化量成正比。从这里我们可以看出,电子管在这种情况下,对交流分量来说就像是一个电阻,事实上这就是电子管的内阻R\(_{i}\)。然而在放大器中不能这样简单地把电子管仅仅看成是一个电阻,因为栅极上还加着交变电压Ug~,这个电压就像一个发电机那样在屏极电路产生交变电流。大家知道,栅压对屏流的影响为屏压对屏流的影响的μ倍。这里μ是电子管的放大因数。设一个电子管的μ=20,这样,如果在栅极加一个交流电压U\(_{g~}\),能在屏极中产生振幅为1毫安的交流电流,那么,如果把Ug~不接在栅极而直接接在屏极电略中,屏极中产生的交流电流振幅就只有1/20毫安了。要想使交流屏流的振幅仍为1毫安,屏路中所加的交流电压就应当增加大到μ\(_{Ug~}\)=20Ug~。由此可见,加到栅极的交流电压U\(_{g~}\)在屏路中造成的交流屏流,正等于把一个μUg~的交流电压发生器接在屏路中一样。
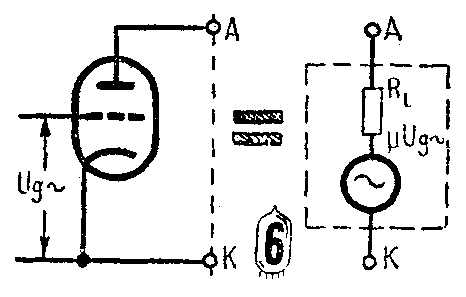
从上面的分析可以知道,如果不考虑电子管中的直流分量而只考虑电子管对交流分量的作用,那么电子管相当于一个发电机μU\(_{g~}\)和一个电阻Ri串联,如图6所示。这个电路就是电子管的交流等放电路。当然,各电极上的实际电流和电压,是交流成分再加上各极原有的直流电压或电流。但是,这些直流电压或电流的目的,仅在于配置电子管在特性曲线上的工作点,而放大作用则表现在交流成分。所以等效电路内只考虑交流成分而不考虑直流成分。
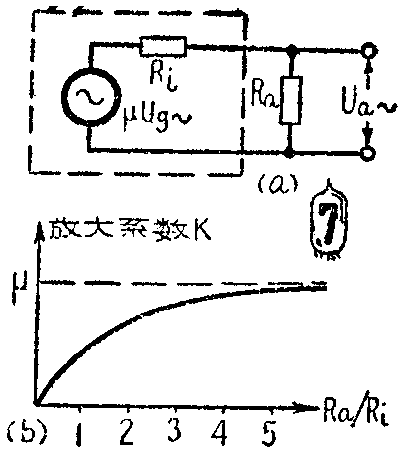
将图4a中的电子管用它的等效电路代替,就得到这个放大器的交流等效电路,如图7a所示。由图中看到,输出电压U\(_{a~}\)实际上就是μUg~通过内阻R\(_{i}\)和Ra所组成的分压器在R\(_{a}\)上所分到的电压,根据欧姆定律,流过Ra的电流为
I\(_{a~}\)=μUg~R\(_{i}\)+Ra,
那么电阻R\(_{a}\)上的压降等于
U\(_{a~}\)=Ia~R\(_{a}\)
=\(\frac{μU}{_{g~}}\)Ri+R\(_{a}\)·Ra。
这样,放大器的放大系数就等于
K=\(\frac{U}{_{a~}}\)Ug~=μR\(_{a}\);Ri+R\(_{a}\)。
从这个式子中我们看到,放大系数不但和所用的电子管的参数有关,(μ越大、放大倍数越大),而且还和R\(_{a}\)的大小有关。Ra越大,放大系数就越大。这是很明显的:因为R\(_{a}\)大,Ra上分到的电压U\(_{a~}\)也大了。
但是放大系数和R\(_{a}\)并不是成正比关系,无论Ra多么大,放大系数K也决不会大于电子管的放大因数μ,因为R\(_{a}\)上能够分到的电压Ua~最大也不过是μU\(_{g~}\)。图7b画出了K和Ra的关系。从这里我们可以看到,实际上当R\(_{a}\)=(3~5)Ri时,放大系数K就很接近μ了,再增大R\(_{a}\)时,K的增加就不大了,因此,三极管的交流负载电阻一般就选择在(2~5)Ri这个范围内。
对于五极管放大器,由于五极管内阻是很大的,一般来说比R\(_{a}\)要大得多,这样放大系数的公式就可以简化为:
K=\(\frac{μR}{_{a}}\)Ri+R\(_{a}\)≈μ;RiR\(_{a}\)=SRa,
其中S是电子管的跨导。
上面我们介绍了电子管放大器的工作原理。虽然讨论的是最基本、最简单的电路,但是其它更复杂的电子管放大器电路也都是应用这种基本原理工作的。因此掌握这些基本原理将为进一步掌握复杂的电路提供必要的条件。(莫愁)