晶体管的特性曲线

大家知道，电子管的性能可以用静态特性曲线来描述。可以利用静态曲线族用图解法求得电子管的参数，分析电子管的放大作用，进行放大器的计算。晶体管也是一样，因此就需要了解和掌握晶体管的特性曲线。电子管在没有栅流的甲类工作时，有两种静态特性曲线族。一种是描述屏流和屏压间的关系（栅压保持不变）的输出特性曲线，一种是描述栅压变化对屏流影响（屏压保持不变）的转移特性曲线。这两种曲线族不是相互独立的。有了一种曲线族就可以经过转换得出另一曲线族。所以进行电路的图解分析时，只需用其中的一种特性曲线族就可以了。在晶体管的情况下，由于有输入电流（发射极电流I\(_{e}\)或基级电流Ib)，而且输出端对输入端有一定的反馈作用，因此，除了和上述两种电子管特性曲线类似的特性以外，还有描述输入电流和输入电压间的关系的输入特性曲线，以及描述输出电压（或电流）对输入电压（或电流）影响的反馈特性曲线，或叫反向转移特性曲线。这两种曲线族也不是相互独立，而是可以相互转化的。由此可见，晶体管一共有四种特性曲线族。在进行晶体管的电路分析时，也只需要其中的一半即两种独立的曲线族就够了。通常需要的是输出特性曲线族和输入特性曲线族。

在第3期“晶体管的低频参数和等效电路”一文中曾经说过，如果把晶体管看作一个四端网络，它的输入端电压和电流分别为u\(_{1}\)和i1，输出端电压和电流分别为u\(_{2}\)和i2，那末，视采用那两个变数为自变数，可以得到不同的等效电路和参数组。与此相应，若取i\(_{1}\)，i2为自变数，可得出四个特性曲线族，称为阻抗系曲线族；若取u\(_{1}\)，u2为自变数，也可以得出四个特性曲线族，称为导纳系曲线族；若取i\(_{1}\)和u2为自变数，又可以得到另外四个特性曲线族，称为h系曲线族，又叫杂系曲线族。这种情况如表1所示。这三种体系的特性曲线，都可以用来表明晶体管的特性，计算晶体管的电路。其中以h系曲线族用得较多，现在就来进一步谈谈这种特性曲线。

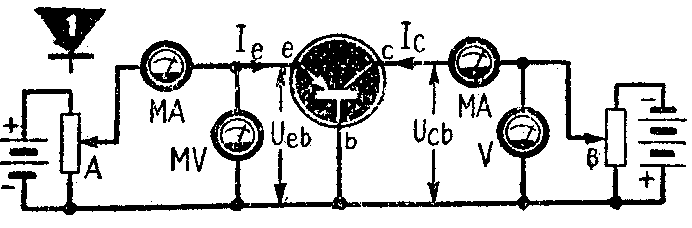
晶体管有共基极、共发射极、共集电极三种连接方法。接法不同，测绘出的特性曲线族也不相同。一个PNP型晶体管，例如П6，接成共基极电路，并象图1那样接上电源电压以及电流表和电压表，就可以测出它的共基极静态特性曲线族。例如，测绘h系输出特性曲线时，调节电位器B以改变U\(_{cb}\)，同时调节电位器A使Ie保持不变，测得对应的I\(_{c}\)值，就可以得出一条Ic～U\(_{cb}\)（Ie=常数）的输出特性曲线。如果使I\(_{e}\)保持为另一常数值，就可以得到另一条Ic～U\(_{cb}\)曲线。结果得出如图2a所示的输出特性曲线族。如果调节电位器A以改变Ie,并同时调节电位器B使U\(_{cb}\)保持不变，测得对应的Ueb值，就可以得出h系输入特性曲线。保持U\(_{cb}\)为不同的常数，就可以得到h系输入特性曲线族，即Ueb～I\(_{e}\)（Ucb=常数）的曲线族，如图2b所示。

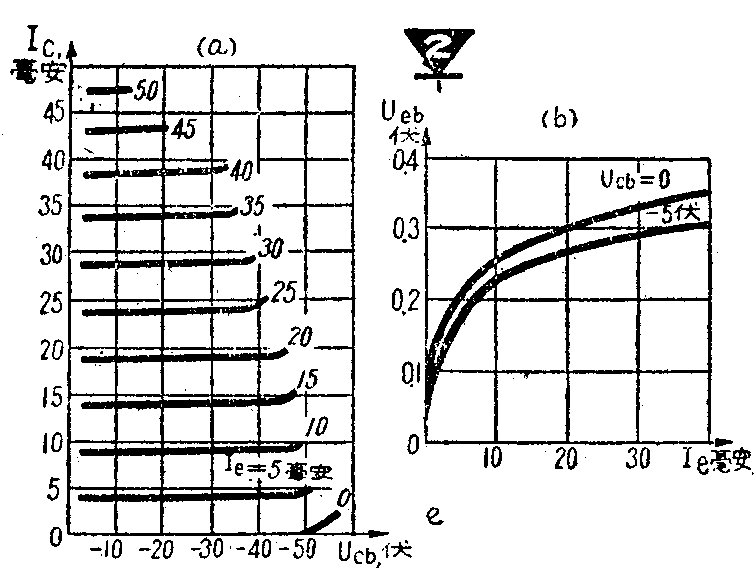
由图2a可以看到，晶体管的h系输出特性曲线族和理想的五极管的屏极特性曲线族很相似。I\(_{e}\)=0时，发射极没有载流子注入基极，所以这时的Ic就是集电结的反向电流I\(_{co}\)。Ie=0的曲线（I\(_{co}\)曲线）就是集电结反向伏安特性曲线。Ico的数值很小，而且在很小的U\(_{cb}\)时即已饱和，所以它是几乎和轴重合的一条直线。当有发射极电流时，发射极向基极注入载流子，并到达集电极，于是Ic=I\(_{co}\)＋αI-e，这里α是-直流电流放大系数。这时的输出特性曲线等于将I\(_{co}\)曲线向上平移了αI-e的间隔。I\(_{e}\)增加一定的数值，曲线就成比例地向上移一段间隔。因此，图2a中各曲线相互平行，而且间隔均匀。这说明输出特性的非线性失真很小。Ic值稍小于I\(_{e}\)，说明共基极的直流电流放大系数α是-稍小于1的。

在图2b的h系共基极输入特性曲线族中，U\(_{cb}\)=0的曲线相当于发射结的正向伏安特性曲线。当集电极加有反向电压时，曲线稍微向移开一些，也就是说，在同样的发射极电压Ueb下，增加集电极反向电压对发射极电流I\(_{e}\)稍微增大一些。这说明集电极电压对发射极电流有了反作用，也就是晶体管内部的反馈作用。

图3是上述晶体管的共发射极连结电路，由此可绘出晶体管的共发射极静态特性曲线族。现在以输入电流即基极电流I\(_{b}\)和输出电压即集电极电压Uce为自变数来描绘曲线，可得出图4所示的四种h系数特性曲线族。

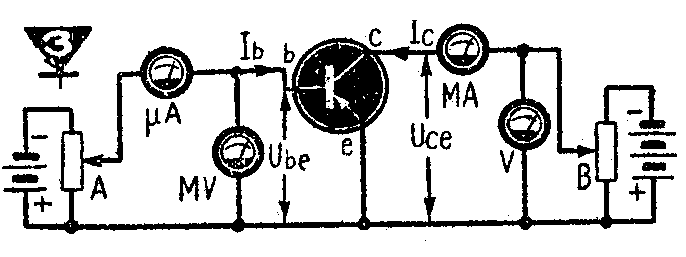
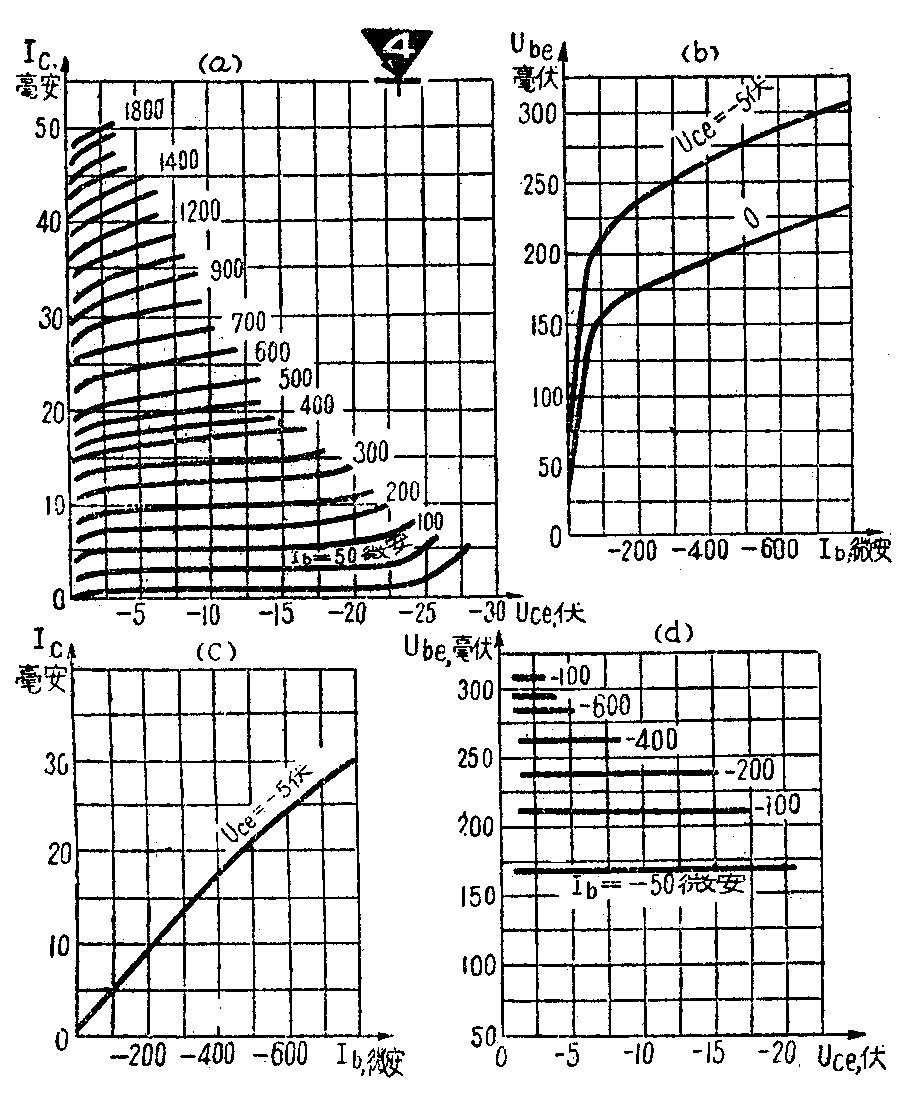
图4a示输出特性曲线族（I\(_{c}\)～Uce，I\(_{b}\)=常数）。它和五极电子管的屏极特性曲线族很相似。而且在使用电子管时利用特性曲线来分析电路和求出低频参数的一些方法，对于晶体管的情况在原则上也是适用的。由图可见，这些曲线随Uce的增加而缓慢上升，原因是U\(_{ce}\)中有一小部分电压是正向加在发射结上的，因此随着Uce的增加，发射结正向电压加大，集电极电流随之增大。

图4b示输入特性曲线族（U\(_{be}\)～Ib，U\(_{ce}\)=常数），当Uce=0时，集电极和发射极短接，集电结和发射结并联，并加有正向电压，所以U\(_{ce}\)=0的曲线相当于晶体二级管的正向伏安特性曲线。当Uce不等于零时，集电结加有反向电压，就有反向电流I\(_{co}\)流过基极引线，其方向和Ib相反，所以使I\(_{b}\)减小，因而曲线就向左移动了。

晶体管的h系共发射极正向转移特性，即电流放大特性曲线（I\(_{c}\)～Ib，U\(_{ce}\)=常数）示于图4c。反向转移特性即反馈特性曲线族（Ube～U\(_{ce}\)，Ib=常数）示于图4d。

前面说过，电子管可以从它的静态特性曲线族求出参数μ，r\(_{p}\)，gm等。同样，晶体管也可以从它的静态特性曲线族求出低频参数。例如，利用h系共基极静态特性曲线族，可以直接求得晶体管的共基极h参数。利用输出特性曲线族可以求得h\(_{22}\)和h21，利用输入特性曲线族可以求得h\(_{11}\)和h12。

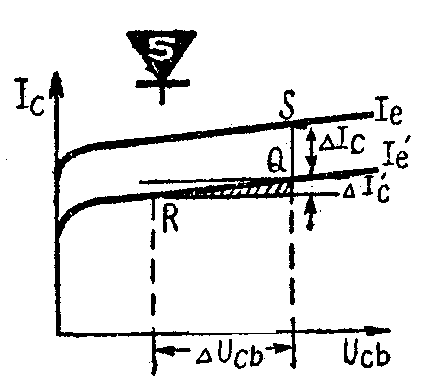
图5示h系共基极输出特性曲线族。设我们求工作点Q处的参量。令点Q沿I＇\(_{e}\)曲线变化到R，此时Ic变化一个数值ΔI＇\(_{c}\)，Ucb变化一个数值ΔU\(_{cb}\)，而Ie保持不变（ΔI\(_{e}\)=0），相当于发射极交流电流为0，或者说对交流电流是开路的。因此h22=\(\frac{ΔI＇}{_{c}}\)ΔUcb，即为输入端开路时的输出电导。相似地，若令Q点沿垂直线变到S，此时U\(_{cb}\)保持不变，对交流而言，相当于输出端短路，而Ic变化了ΔI"\(_{c}\)，Ie变化了I"\(_{e}\)-I＇e=ΔI\(_{e}\)，所以h21=ΔI"\(_{c}\)ΔIe，即为输出端短路时的电流放大系数。

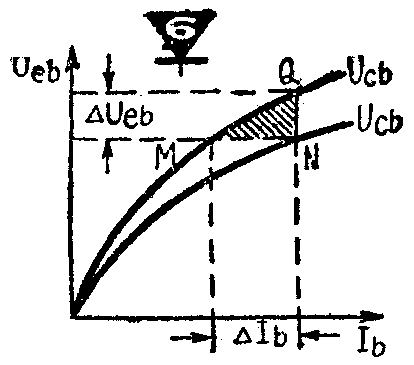
图6示h系共基极输入特性曲线族。Q为工作点。设Q沿U"\(_{cb}\)线变到M，此时Ucb不变，U\(_{eb}\)变了ΔUeb，I\(_{b}\)变了ΔIb。因此h\(_{11}\)=ΔUebΔI\(_{b}\)，即为输出端短路时的输入电阻。而当Q沿垂直线变到N时，Ib保持不变，U\(_{cb}\)从U"cb变到U＇\(_{cb}\)，即变化了ΔUcb=U"\(_{cb}\)-U＇cb，U\(_{eb}\)变化了ΔUeb，所以h\(_{12}\)=ΔUeb;ΔU\(_{cb}\)，即为输入端开路时的电压反馈系数。

和求h参数的情况相似，根据阻抗系特性曲线族和导纳系特性曲线族也可以分别求出晶体管的低频电阻参数和电导参数来。（于闻）