普通线路阻抗为600欧。但有些音频振荡器的输出阻抗不等于600欧。为了对线路及载波有线广播中的滤波器等进行测试,必须使振荡器的输出阻抗和它们相匹配。为此就要加一装置以获得匹配。并且保证一定的输出电压(15伏以上)。
可以加一匹配网络来进行匹配,但它有衰减,输出电压常不能满足要求。用变压器也能达到阻抗匹配的目的,但它的造价高,同时很难做到较宽频率的放大。利用简单的阻容耦合放大器,加以适当的负反馈,可以作为阻抗匹配装置。它既能达到匹配,又能保证足够的输出电压。
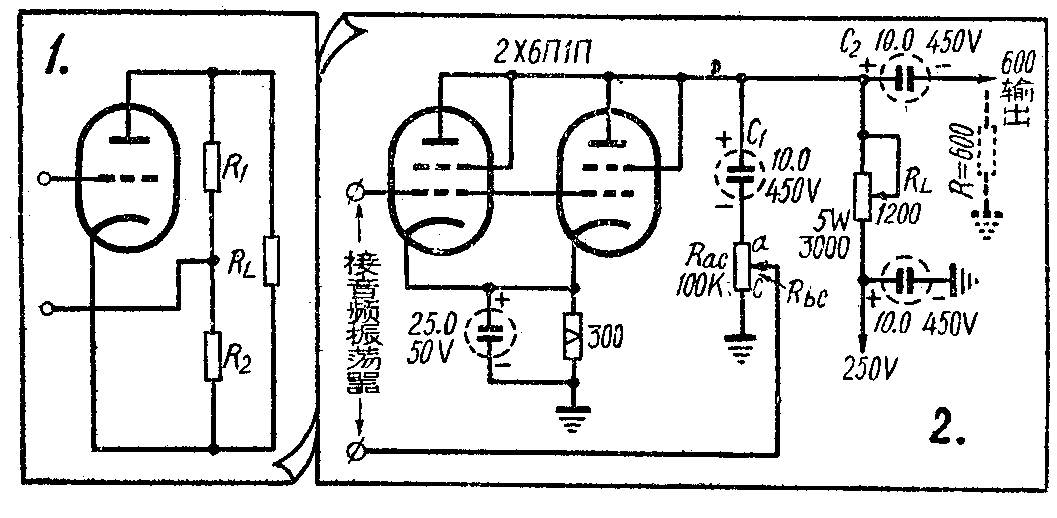
图1绘出了电压负反馈放大器的原理图。这时电子管的等效内阻r′;将降低:
r′\(_{i}\)=ri1+μβ(1)
式中μ是电子管的放大因数,r\(_{i}\)是电子管的内阻,β=R2R\(_{1}\)+R2是反馈系数。由上式可见,反馈越深(β越大),得r′\(_{i}\)降得越低。把上式中的β解出得:
β=\(\frac{r}{_{i}}\)-r′iμr′\(_{i}\)。(2)
从(2)式可以看出,当电子管选定时(即r\(_{i}\)和μ已知),可以根据所需要的有效内阻r′i来选取反馈系数β。
图2画出了一个实际线路。为了获得足够的输出,采用了两个6ПlП并联。图中C\(_{1}\)、C2为隔直流电容器,R\(_{ac}\)为反馈用的电位器, RL为屏极负载电阻,虚线所示的R代表所测线路或设备的电阻。
从6П1П管的特性表中查出内阻为42.5千欧,互导为4.9毫安/伏,放大因数为42.5×4.9=208。两管并联后的总内阻等于单管时的一半,即r\(_{i}\)=12×42.5=21.25千欧。
我们选用屏极负载电阻R\(_{L}\)=1.2千欧。为了获得匹配,必须使放大器的输出电阻,即r′i和R\(_{L}\)并联的电阻(Rac很大可以忽略不计)等于外阻R=600欧。也就是说
因而r′\(_{i}\)=RRLR\(_{L}\)-R=600×1200;1200-600=1200欧。
把这些r\(_{i}\)、R′i和μ的数值代入(2)式得
β=\(\frac{r}{_{i}}\)-r′iμr′\(_{i}\)=21.25-1.2;208×1.2=0.08。
即需要有β=0.08的负反馈才能满足要求。因为反馈电位器R\(_{ac}\)=100千欧,所以应把电位器调整到Rbc=100000×0.08=800欧。
选定β以后,应计算一下该反馈放大器的放大系数K\(_{f}\),看是不是能满足要求。设V是音频振荡器的输出电压,必须使KfV>15伏。
在图2的线路中,当β=0时,即没有反馈时的放大系数为
K=\(\frac{μR′}{_{L}}\)(R′L+r\(_{i}\)),
其中R′\(_{L}\)应该是等于RL和R的并联结果:
R′\(_{L}\)=RLRR\(_{L}\)+R=1200×600;1200+600=400欧。
因而 K=\(\frac{208×400}{21250+400}\)=4.06。
当有反馈,而β=0.08时
K′=K(1+Kβ)=4.06;1+0.08×4.06=3.07。
由此可见,如果音频振荡器输出大于5伏,就可以满足要求。上述线路经实验证明可以满足匹配的要求,在20赫~100千赫的范围内,输出电压不低于15伏。
如果计算出的K\(_{f}\)不够大,可以把屏极负载加大些以增大输出电压,同时要重新计算β以使输出电阻为600欧。(屏比)