电容和电感的测量

线圈和电容器是无线电设备中的两种主要元件。在装配无线电设备时,首先要知道线圈的电感和电容器的电容数值。在这篇文章里，我们将介绍测量线圈电感和电容器电容等的一些简单的方法。

测量电感有三种主要方法：电压表和电流表法、电桥法、谐振法。

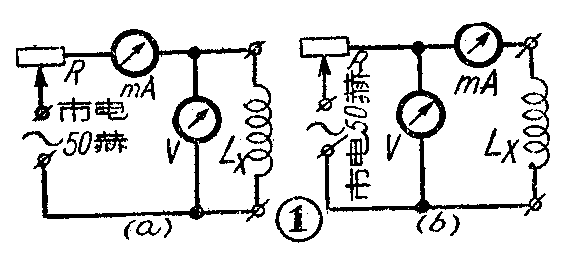
（1)电压表和电流表法。这种方法可以用来测量较大的电感，如低频扼流圈等。测量时，可用图1的线路及50赫的交流电源。读出毫安表的读数I和电压表的读数V。设线圈的电阻r可以忽略，则因为在线圈两端的电压降V=（2πfL\(_{x}\)）I，所以

如果所用的电压表内阻很高，可以用图1a的线路；如果电压表内阻较低，就应当用图1b的线路。

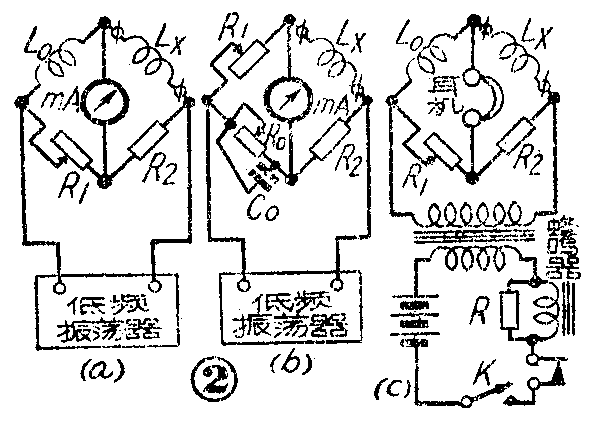
（2）电桥法。用电桥法可以测量几微亨到几十亨的电感，它的电源可采用800～1000赫的低频振荡器。桥路中可以利用标准电感L\(_{0}\)（图2a)或标准电容C0（图2b)。在电桥对角线上可以用毫安表，也可以用耳机来代替；如果没有低频振荡器，也可以用蜂鸣器，如图2c所示。

测量时，调节电阻R\(_{1}\)（在图2b中调节电阻R1及R\(_{0}\)），使毫安表读数或耳机中的声音达到最小。此时电桥平衡。如果采用图2a的线路时，所测电感应为Lx［微亨]=L\(_{0}\)[微亨]R2[欧]/R\(_{1[欧]}\)。如果采用图2b的线路时，所测电感应为Lx[微亨]=C\(_{0}\)［微法]×R1[欧]×R\(_{2[欧]}\)。图2b中的可变电阻R0用来补偿相反桥臂上的相角，使电表的最小读数更为明显。

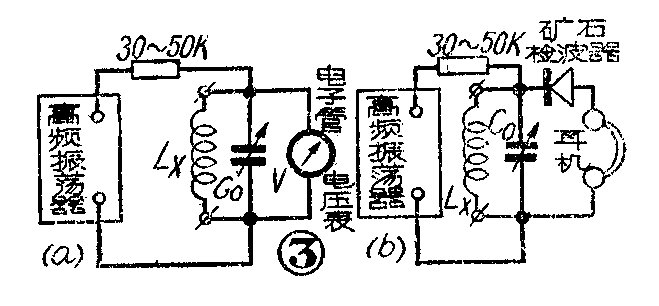
（3）谐振法。谐振法可以测量很小的高频线圈电感。测量线路如图3a。为了使高频振荡器和振荡回路保持松耦合，要串联一个30～50千欧的电阻。图中的C\(_{0}\)为有刻度的标准电容器。

测量时，调节电容器C\(_{0}\)使电子管电压表的读数为最大，即使回路达到谐振。这样，利用公式ω\(^{2}\)=\(\frac{1}{KC}\)，可得所测电感为

用上式计算电感时，并没有考虑到线圈本身的潜布电容C\(_{A}\)。因为在大多数情况下，这个电容是可以忽略的。如果线圈的潜布电容很大，则可按下式来计算：

测定式中的C\(_{A}\)时，将电容器调到和前面不同的刻度C0′上，再调节高频振荡器使电子管电压表的读数最大，记下这个谐振频率f′，则C\(_{A}\)可按下列公式算得：

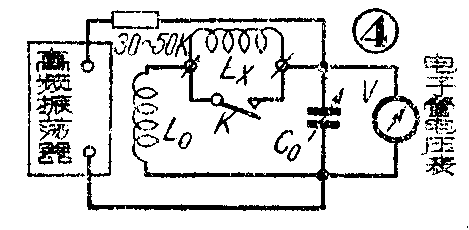
图4是谐振法的另一种电路，可以测量更小的电感。测量时，先将开关K接通，调节电容器C\(_{0}\)使电子管电压表的读数最大,记下这个电容为C01。然后将开关K断开，即将被测电感接上，再调电容器C\(_{0}\)使电子管电压表的读数最大，记下此时的电容为C02。这样，所测电感为

式中的f是高频振荡器的频率。

图4中L\(_{0}\)的数值应选用和Lx具有相同数量级的。

在用谐振法测量时，如果没有电子管电压表，也可以用一个矿石检波器和耳机并接在振荡回路上以监测谐振，例如图3b所示的情况。不过这时高频振荡器的输出要用已调幅的信号。

测量电容的方法很多，下面只介绍几种常用的方法。其中有些是和测量电感的方法大体上相同的。

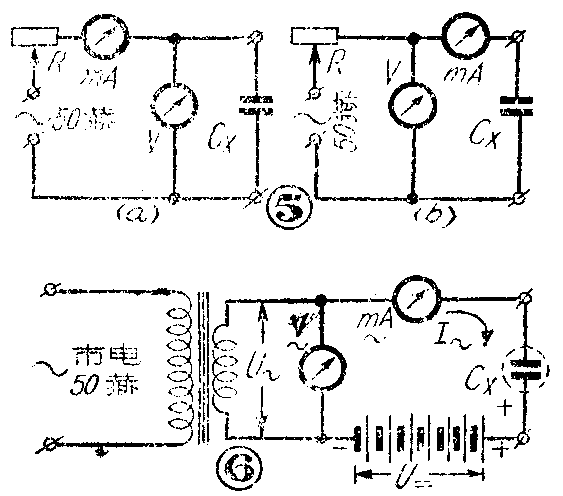
(1)电压表和电流表法。这种方法可以测量大于0.1微法的电容。测量电路如图5所示，测量方法和图1测电感的方法相同。因为

若所用电源为50赫的市电，则

如果要测量电解电容器，应当采用图6的电路。电路中的直流电压（用电池或蓄电池）是用来保持电容器的极性的，电压大小最好等于电容器的工作电压。交流电源可以采用50赫的市电，通过变压器来供电，交流电压值要小于直流电压很多，以免破坏电解电容器的极性，一般可采用4～6伏。所用毫安表应当只能测量交流电流，而对直流电流没有反应。在这种情况下,仍按前一公式计算。

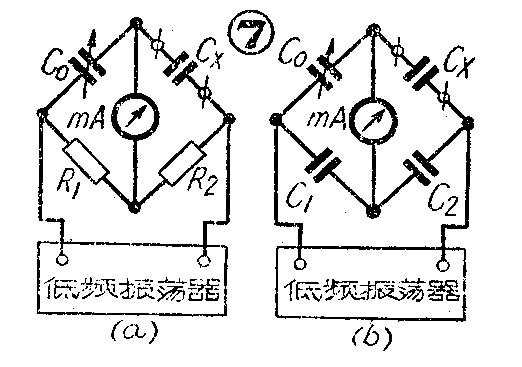
（2）电桥法。一般的测量线路有图7所示的两种。测量时，调节电容器C\(_{0}\)，使毫安表的读数最小（或耳机中的声音最小）。如用图7a的电路，被测电容为Cx=C\(_{0}\)R1／R\(_{2}\)，如果用图7b的电路，则Cx＝C\(_{0}\)C2／C\(_{1}\)。

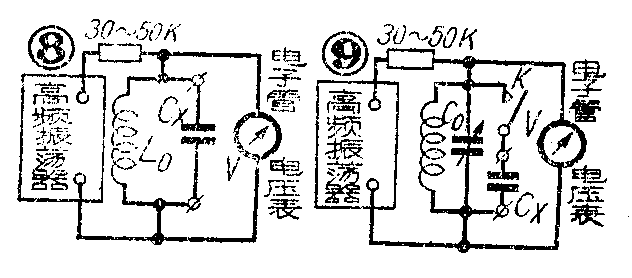
（3）谐振法。要测量几个微微法到几千个微微法的电容时，可用谐振法（图8和图9）。测量时，如果采用图8的线路，应调节高频振荡器的频率，使电子管电压表的读数最大，这时，所测电容为：

C\(_{x[微微法]}\)=2.53×10\(^{1}\)0;f2[千赫]L\(_{0}\)[微亨]。

假如所测的电容很小，为了避免线圈的潜布电容和接线电容的影响，可以采用图9的线路。先将开头K断开，调节高频振荡器频率使电子管电压表的读数最大，记下此时标准电容的电容量为C\(_{0}\)1。然后关上开关使被测电容Cx和C\(_{0}\)并联，为了重新达到谐振，就需要把标准电容减小到C02。C\(_{0}\)1和C02的差就是C\(_{x}\)的数值。

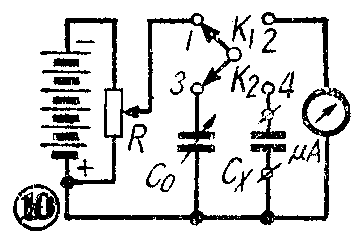
（4）冲击法。此法可以测量大的电容，其线路如图10所示。测量时，先把K\(_{1}\)放在位置1，把K2放在位置4，将电位器R的旋臂放在电压较低的位置（例如2伏左右），使电容器C\(_{x}\)充电。然后把开关K1扳到位置2，使电容器通过微安表放电。如果微安表偏转过小，可以调节电位器的旋臂，适当增高充电电压，直到微安表的指针差不多能摆动到全刻度时为止。这时要记下指针的最大偏转值。然后将开关K\(_{2}\)转到位置3，和标准电容器C0相连。在充电电压不变的情况下（即电位器旋臂固定不动），扳动K\(_{1}\)对C0作充放电实验。调节C\(_{0}\)的数值，使C0通过微安表放电时所发生的偏转，和刚才待测电容器放电时所得的偏转一样。这时，被测的电容C\(_{x}\)就和标准电容C0相等。

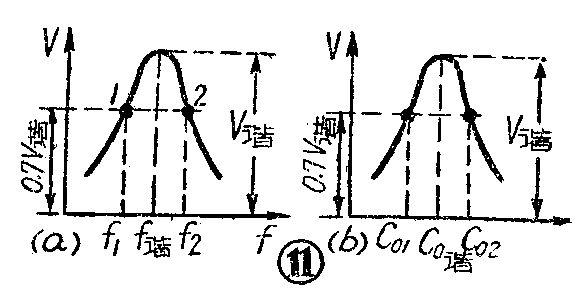
（1）Q值的测量。测量高频线圈的Q值时，可利用谐振曲线法。利用图3的线路，保持C\(_{0}\)不变，改变高频振荡器频率f,并记下对应的电子管电压表读数V,即可得到图11a的谐振曲线；如果保持f不变而改变C0，即可得到图11b的谐振曲线。

经过V=0.7V\(_{[谐]}\)的地方画一条平行于横轴的直线，交谐振曲线于1、2两点。自1、2两点分别引垂线交横轴于f1、f\(_{2}\)两点（在图11b中为C01、C\(_{0}\)2两点）。此时，对于图11a的情况，

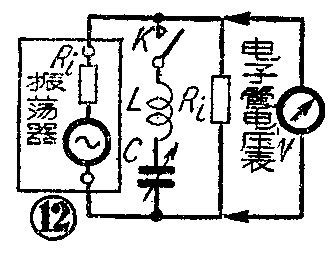
测量低频线圈的Q值时，可利用衰耗法和代换法。衰耗法的线路见图12。选一内阻为R\(_{i}\)（600欧）的振荡器，终接一等于Ri的纯电阻。先将K断开，用电子管电压表量所接电阻上的电压为V\(_{1}\)。然后关上K,使谐振电路接入，用电子管电压表量LC谐振时的电压为V2。这时

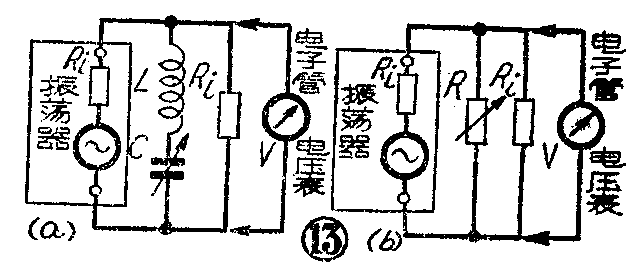
比较法的线路见图13。先如图13a那样测得LC谐振时的电压为V\(_{1}\)，然后用一可变电阻R代替LC（见图13b）。调节可变电阻，使电压表上的读数仍为V1，记下此时的电阻R，则

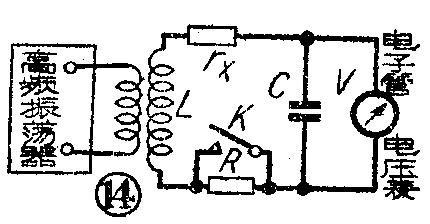
（2）振荡回路等效电阻的测量。线路如图14所示。高频振荡和回路之间要保持松耦合。测量时，先关上开关K使R短路，调节高频振荡器频率使电压表读数最大，并记下此读数为V\(_{1}\)。然后将开关K断开，接入已知的附加电阻R，再改变振荡器频率使电压表的读数最大，并记下这个电压为V2。这时，回路的等效电阻为

（高煜）