双稳态触发电路是脉冲技术中最基本的电路之一,它在无线电电子学的各个领域,例如测量技术、电视和电子计算机中都获得了极为广泛的应用。
什么是双稳态触发电路呢?我们举一个简单的例子来说吧。例如有一个普通的电灯开关,它就有“开”(接通)和“关”(断开)两个稳定状态,或者叫做双稳态。当用手把开关扳到“开”的位置时,电灯就亮了。这个状态是稳定的,除非把开关再扳到“关”的位置,电灯将一直亮着。同样地,当电门在“关”的位置时,如果不去扳动它,电灯就永远不会亮。扳动开关就是对开关进行“触发”。因此,装有普通开关的电路,广义地说,也可叫做双稳态触发电路。
这里介绍的双稳态触发电路也是具有两个稳定状态。要使电路从一个稳定状态转变为另一个稳定状态,不是用手去“触发”。而是用外加的脉冲电动势对电路进行触发。这个脉冲通常叫做触发脉冲。
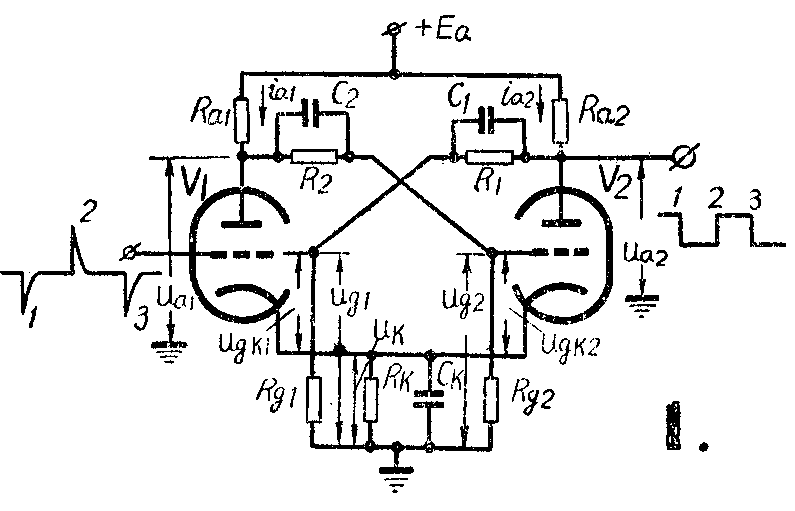
图1所示为应用很广的屏栅耦合双稳态触发电路。这个电路的两个稳定状态是:(1)V\(_{1}\)通过很大的电流而V2截止;(2)V\(_{2}\)通过很大的电流而V1截止。
为了简单起见,我们假设这个电路是完全对称的:三极管V\(_{1}\)和V2的参数完全一样,并且R\(_{a1}\)=Ra2,R\(_{1}\)= R2,C\(_{1}\)=C2,R\(_{g1}\)=Rg2。初看起来,这个电路好象是处在平衡状态,两个电子管中的电流i\(_{a1}\)和ia2应当相等。但是,这种平衡状态是不稳定的。电路不能处在这一状态,而一定要转到上述两个稳定状态中的任一个状态去。就象尖端朝下竖立着的铅笔一样,即使把它放得完全垂直,完全对称,它也不能稳定地立在那里。一受到任何偶然原因的影响(震动、空气的吹动等),它就会倒下来。
例如,我们假定由于某种偶然的原因(电源电压的微小变化或者外界的机械振动等)使电子管V\(_{1}\)的屏流ia1有了很小的增加,那么R\(_{a1}\)上的电压降ia1R\(_{a1}\)就随着增加了。V1的屏压u\(_{a1}\)= Ea-i\(_{a1}\)Ra1就相应地减小。但是,电子管V\(_{2}\)的栅极电压ugk2是由电阻R\(_{k}\)上的负电压降uk和R\(_{g2}\)上的正电压降ug2合成的,而u\(_{g2}\)又和ua1成正地〔u\(_{g2}\)=ua1R\(_{g2}\)/(R2+R\(_{g2}\))〕,所以ua1的减小使得u\(_{gk2}\)减小。这样就使电子管V2的屏流i\(_{a2}\)减小,ig2R\(_{a2}\)减小,因而使V2的屏压u\(_{a2}\)增高。ua2的增高通过R\(_{1}\)Rg1的分压器作用到电子管V\(_{1}\)的栅极,使ug1增加〔u\(_{g1}\)=ua2R\(_{g1}\)/(R1+R\(_{g1}\))〕 这就使得ia1进一步增加。我们看到,由i\(_{a1}\)的偶然增加起,兜了一个圈子,又使ia1更进一步增加。这个圈子是:i\(_{a1}\)增加→ua1减小→u\(_{g2}\)减小→ia2减小→u\(_{a2}\)增加→ug1增加→i\(_{a1}\)更进一步增加。
但是过程并不就此结束。i\(_{a1}\)既然进一步增加了,它就会再经过上面的圈子使ia2继续减小,使i\(_{a1}\)继续增加。就象一个小雪球从山上滚下来一样,体积越来越大,速度越来越快,直到滚到山脚下为止。上述兜圈子的过程也是以很快的速度继续进行下去,或者说雪崩式地发展下去。如果Rk选得相当大,使得R\(_{k}\)上的负偏压uk在电子管的截止偏压以下,那么,当i\(_{a1}\)增大使ua1不断降低时,u\(_{g2}\)上的正电压就会降低到这样的程度,以至于它和uk的合成电压u\(_{gk2}\)降低到电子管V2的截止偏压值。这时电子管V\(_{2}\)截止,ia2减小到零,不能再减;电子管V\(_{2}\)的屏压ua2增加到差不多等于电源压E\(_{a}\),不能再加。于是,上述雪崩过程就终止了。
就这样,电路转入了它的第一个稳定状态,就是V\(_{1}\)通流而V2截止的状态。在这种状态下,电子管V\(_{2}\)的栅压ugk2降到截止偏压以下,i\(_{a2}\)=0,ea2≈E\(_{a}\)。电子管V1的栅压u\(_{gk1}\),由于ea2这个差不多等于E\(_{a}\)的高电压通过分压器R1R\(_{g1}\)加到V1的栅极,本来也应该是很高的正压。但是,因为栅极为正时会出现栅流,这好象是在电子管内用一个不大的电阻把栅极和阴极接通了,所以u\(_{gk1}\)是增加不上去的,它只能增到比零稍高的地步,或者粗略地说,ugk1≈0。在这种情况下,i\(_{a1}\)增加到很大的数值(ia1最大),而屏压u\(_{a1}\)就降到很小的数值(ua1最小)。这个状态是稳定的,如果不对电路进行“触发”,它就会一直处于这一状态。
和上面叙述的情况相似,如果在开始时不是i\(_{a1}\),而是ia2有了偶然的增加,那么,电路就会雪崩式地转到第二个稳定状态,即电子管V\(_{1}\)截止,电子管V2通过很大电流的状态。在这种状态下。电子管V\(_{1}\)的栅压ugk1降到截止偏压以下,i\(_{a1}\)=0,ua1≈E\(_{a}\)。电子管V2的栅压u\(_{gk2}\)≈0,ia2增到最大,u\(_{a2}\)降到最小。
在所述的电路中, 在电阻R\(_{1}\)、R2上分别并联一个电容器C\(_{1}\)和C2,它们的作用是使上述雪崩过程更快地进行。大家知道,电容器在充电或放电时,它的电压不可能在一瞬间发生跃变,因为这个电压V=CQ,而电荷Q的积累或离去需要一定的时间。因此,在触发电路中,例如当u\(_{a1}\)突然增加一个数值时,并不能使电容器C2上的电压突然增加,u\(_{a1}\)增加的电压就一下子通过C2全部加在R\(_{g2}\)上,使ug2的增加比在没有C\(_{2}\)时大很多倍。同样,当ua1突然减小一个数值时,这个电压变化也会通过C\(_{2}\)全部加在Rg2上,使u\(_{g2}\)的减小比在没有C2时大许多倍。这样就使上述雪崩过程大大地加快了。
要使电路从一个稳定状态转到另一个稳定状态,或者说使电路“翻转”,必须对它进行“触发”。举例说,在通流电子管的栅极加一个负触发脉冲,或在截止电子管的栅极加一个正触发脉冲,就可以使电路“翻转”。
我们假定电路处在V\(_{1}\)通流而V2截止的状态。这时,如果在V\(_{1}\)的栅极加上一个负脉冲(图1中的脉冲1),那么,栅极电位ugk1就要降低,使i\(_{a1}\)减小,而使ua1增加。u\(_{a1}\)的增加将通过R2R\(_{g2}\)传到电子管V2的栅极,使栅压u\(_{gk2}\)增加。如果触发脉冲的幅度足够大,ua1的增加就能够使u\(_{gk2}\)增加到截止偏压以上,使电子管V2通流,即产生了i\(_{a2}\)。一旦产生了ia2,u\(_{a2}\)就要下降(相当于图1中矩形波1处的情况),从而使ugk1进一步降低,使i\(_{a1}\)继续减小。这样,就发生了前面所说的雪崩过程,电路很快地翻转到另一个稳定状态,即V1截止、V\(_{2}\)通流的状态。
这时为了使电路再翻转到原来的稳定状态,需要在截止电子管V\(_{1}\)的栅极加一个正极性的触发脉冲。如果这一脉冲的幅度足以使ugk1增加到截止偏压以上,就会使V\(_{1}\)通流,产生ia1。这样一来,就发生了u\(_{a1}\)减小、ia2减小、u\(_{a2}\)增加(相当于图1中矩形波2处的情况),从而使ia1继续增加的雪崩过程。电路又翻转到V\(_{1}\)通流、V2截止的稳定状态。
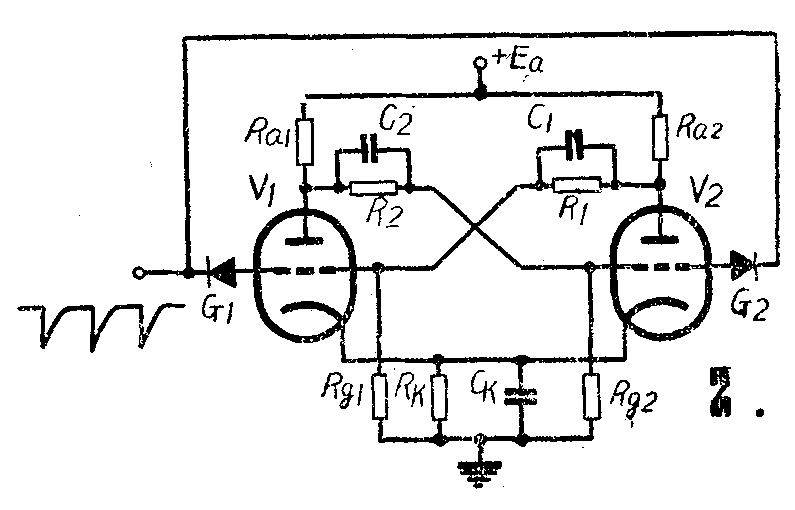
另外一种触发方法是每次翻转都采用同样极性的脉冲,例如负脉冲。这时触发脉冲通过两个隔离二极管G\(_{1}\),G2同时加到两电子管的栅极,如图2所示。这样,当负脉冲到来时,虽然同时加到两个管子的栅极,但是对截止管,例如V\(_{2}\),却不起作用,因为这个管子的负偏压已经在截止值以下,再加负压,V2仍然是处于截止状态。但是负触发脉冲能使通流管V\(_{1}\)的栅压降低,使ia1减小,因而能使电路翻转,也就是使V\(_{1}\)截止而V2通流。在这种状态下,当下一个负触发脉冲到来时。就不对V\(_{1}\)起作用而对V2起作用,使电路翻转到第一个稳定状态。
总结上面所说的情况,可以把双稳态触发电路的工作过程,用图3的时间曲线图来表示。
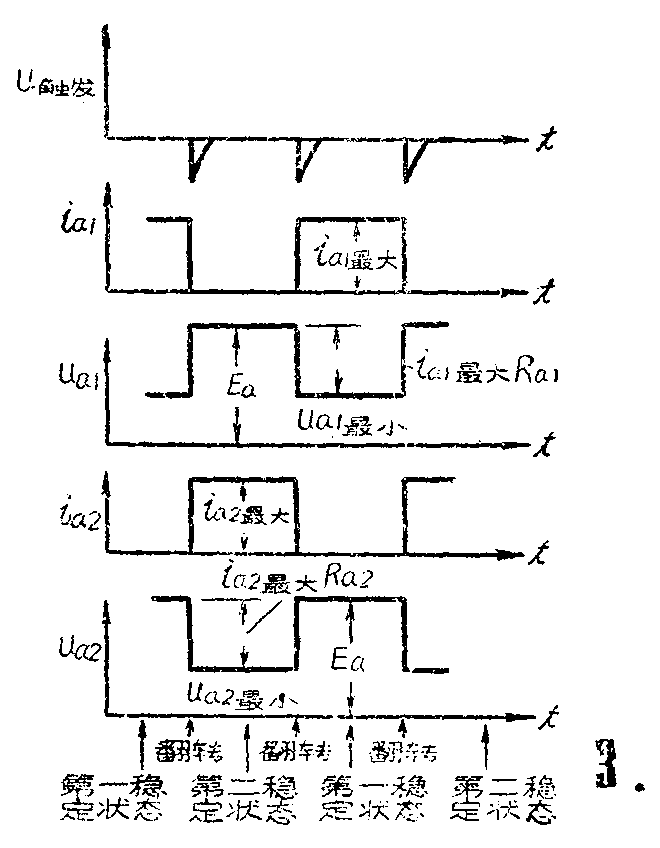
从图3可以看到,利用双稳态触发电路可以在电子管的屏极产生出矩形波。它的幅度很大,形状也很好。改变触发脉冲间的时间间隔,就可以改变这个矩形波的宽度和重复频率。再加上电路很简单,所以这种矩形波发生器在电子学的各个部门中都得到了广泛的应用。
另外,双稳态触发电路是一个很好的电子开关,或者说是一个电子继电器。例如,我们在电子管V\(_{2}\)的屏极电路中接一个继电器,那么,当V2截止时,继电器就不会动作。但一旦有一个触发脉冲使电路翻转时,V\(_{2}\)将通过很大的电流,使继电器动作,继电器的接点就将被控制的电路接通。当下一个触发脉冲到来时,电路翻转,V2截止,继电器释放,被控制的电路就被断开。
双稳态触发电路还可以用作计数器(参看本期“电子计数器”一文),可以在电子计算机中构成运算器和存储器等等。由上面所举的一些例子,就可以看出这种双稳态触发电路的应用是非常广泛的了。(铭)