稳压器是在供电网络电压变化时用来保持负载电压稳定的。本文所述的稳压器的稳压范围为170~250伏,性能较好。
稳压器的原理电路
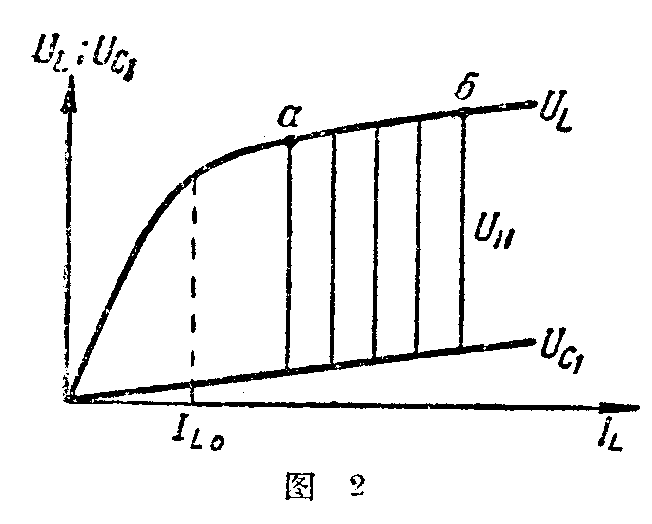
稳压器的原理电路如图1所示。电路的特点是利用电容器C\(_{1}\)来代替通常在磁铁饱和式稳压器中的补偿线圈。
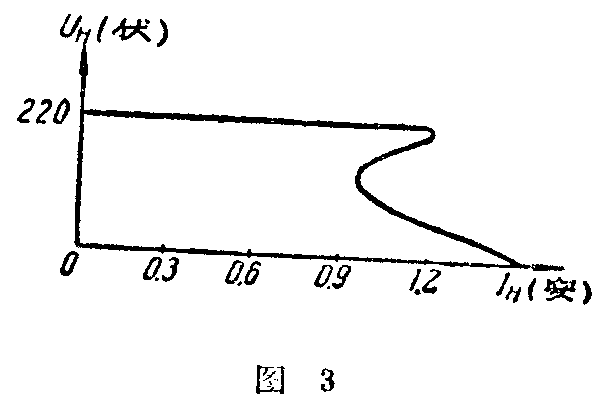
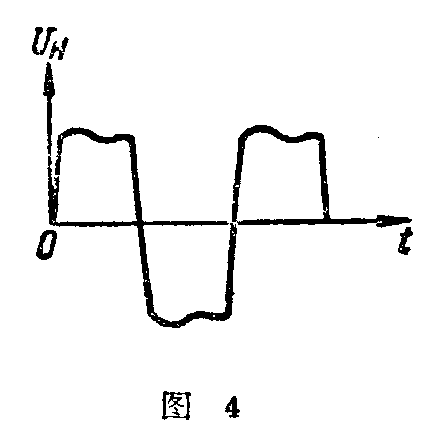
从电路图中可以看出,假定网络电压U\(_{C}\)增大,则流经饱和扼流线圈ДP1的电流I\(_{L}\)也将增大,这时由于铁心已达饱和,所以扼流线圈上的电压UL增高并不多。从图2中U\(_{L}\)和IL的关系曲线可以看出,当I\(_{L}\)增加到达磁饱和电流IL。以后,I\(_{L}\)再增加,UL增加的就很少了。但毕竟还不是稳定不变的,电容器C\(_{1}\)在这里就起着补偿作用。
电容器C\(_{1}\)上的电压UC1=\(\frac{1}{ωC}\)\(_{1}\)IL,电抗1;ωC\(_{1}\)是一个常数,因此UC1是随I\(_{L}\)成正比变化的,UC1与I\(_{L}\)的关系是一根直线,如图2所示。可是由于电容器上的电压UC1的相位和电感上的电压U\(_{L}\)相反,因此负载电压UH的大小就决定于U\(_{L}\)和UC1之差。如果适当地选择电容器C\(_{1}\)的数值,可以使代表UC1和I\(_{L}\)关系的直线,在通过某一段(如图中aб)时与UL和I\(_{L}\)的关系曲线平行。在这种情况下,UL和UC\(_{1}\)之差,也就是负载电压UH(图中用垂直线表示),当I\(_{L}\)或是和它相应的网络电压UC在相当范围内变化时,可以几乎保持不变。
电容器C\(_{2}\)起着平衡电抗的作用。通常在磁饱和稳压器中在这里是采用未饱和的扼流线圈。C2的电抗\(\frac{1}{ωC}\)\(_{2}\)是固定不变的,而饱和扼流线圈的电抗是随着IL的增大而减小的(I\(_{L}\)增加,饱和扼流线圈的电感量L相应地减小,所以电抗ωL降低),因此当网络电压UC增加的时侯,C\(_{2}\)的电抗和ДP1的电抗比较起来就相对的增大了,电容器上的电压UC\(_{2}\)和UL的比值也相对地增大,使增加的电压绝大部分均降落在C\(_{2}\)上,而UL却增加得很少;反过来,当网络电压减小的时候,C\(_{2}\)的电抗和ДP1的电抗比较起来是相对地减小了,UC\(_{2}\)与UL的比值也相对地减小,因此C\(_{2}\)上的电压降低得多,而ДP1上的电压降低很少。这样利用这两个电抗相对比值的变化,就起到稳压的作用。此外,由于用电容器C\(_{2}\)代替了普通磁饱和稳压器中的未饱和的扼流线圈以及利用C2—ДP\(_{1}\)网络接近于电压谐振的方法,当没有变压器或自耦变压器时,可获得较大的负载电压(例如,当网络电压为170伏时负载电压为220伏)。
这个稳压器的功率为200瓦,负载电压的有效值U\(_{H}\)=220伏。扼流圈的铁心用叠厚40毫米的无间隙的Ш—40型的钢片装配,进用Ш—38型钢片较为合适。在这个稳压器中由于采用了有较大窗口的标准钢片(Ш—40),所以叠厚选择的比下面按Ш—38钢片计算所得的叠厚要小。线圈用1.0毫米线径漆包线绕550匝。C1和C\(_{2}\)用小型密封敷金属纸电容器,C1选用耐压160伏的,C\(_{2}\)用500伏的。C1和C\(_{2}\)也可用纸介电容器代替,但稳压器的尺寸就要增大。
满载时稳压器的效率为85%。
稳压器的计算
现计算功率P\(_{H}\)=200瓦,保持负载电压UH=220伏,当供电网络电压从170伏变化到250伏时,负载电压允许脉动为±O.5%的稳压器。
扼流线圈铁心的体积:
Q\(_{C}\)lC=2.3U\(_{H}\)IH=2.3P\(_{H}\)
=2.3×200=460立方厘米 (1)
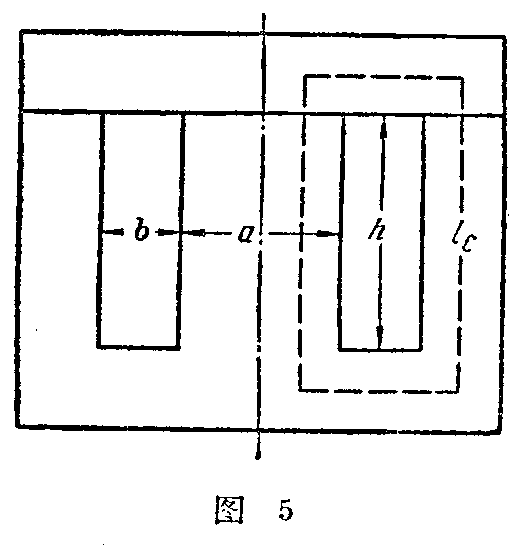
式中,Q\(_{C}\)是铁心中间心柱的有效横截面积,lC是磁路的平均长度(图5)。
钢片的叠厚c应为铁心宽度a的1~2倍,在手册中通常列出各种Ш型钢片叠厚c=(1~2)a时的Q\(_{C}\)lC值。Ш—38型钢片叠厚c=(1—2)a时的Q\(_{C}\)lC=(276~552)立方厘米,而根据上面算出的扼流圈铁心体积应为460立方厘米,因此采用Ш—38型钢片是合适的。
l\(_{C}\)可由下式求出:
l\(_{C}\)=2(b+h)+\(\frac{πa}{2}\)(2)
Ш—38型钢片:a=3.8厘米,b=0.5a,h=1.5a(见图5)
则 l\(_{C}\)=2(0.5a+1.5a)+\(\frac{πa}{2}\)
=2(1.9+5.7)+5.95=21.2厘米
此时Q\(_{C}\)值计算如下:
Q\(_{C}\)=QCl\(_{C}\)lC=460;21.2
=21.7平方厘米 (3)
根据公式Q\(_{C}\)=0.9ac(系数0.9是考虑到各片间有绝缘层的缘故),可算出钢片的叠厚
C=\(\frac{Q}{_{C}}\)0.9a=21.7;0.9×3.8=6.35厘米
线圈的匝数为:
n=\(\frac{37U}{_{H}}\)QC=37×220;21.7=375匝 (4)
在计算扼流圈线圈中的最大电流之前,应先求出供电网络电压的最大值与最小值之比K和负载电流I\(_{H}\):
K=\(\frac{U}{_{C最大}}\)UC最小=250;170=1.47 (5)
I\(_{H}\)=PHU\(_{H}\)=200;220=0.91安 (6)
根据扼流圈线圈中的最大电流值
I最大=(1.52+1.17\(\frac{U}{_{C最大}}\)UC最小)I\(_{H}\)
=(1.52+1.17×1.47)×0.91
=2.95安 (7)
可求出导线截面积
q=\(\frac{I}{_{最大}}\)3=2.95;3
=0.985平方毫米 (8)
式中:3的单位是安/平方毫米——允许电流密度
导线窗口的占空系数:
K\(_{3}\)=\(\frac{nq}{bh}\)=375×0.985;19×57=0.341 (9)
式中,bh=Q\(_{0}\)——窗口面积。
如果出现K\(_{3}\)<0.25或K3>0.35就应选用Ш形钢片的另一种尺寸并以前述的Q\(_{C}\)lC值重新计算。此时所选择的厚度可能有所改变。
最后确定电容器C\(_{2}\)和C1的电容量及其工作电压U\(_{2}\)和U1:
C\(_{2}\)=4830IHU\(_{H}\)=4830×0.91;220
=20微法 (10)
U\(_{2}\)=2·UH=2×220=440伏 (11)
C\(_{1}\)=\(\frac{1.2×10}{^{7}}\)·lCn2·Q\(_{C}\)
=\(\frac{1.2×10}{^{7}}\)×21.23752×21.7=83微法 (12)
U\(_{1}\)=C2·U\(_{2}\)C1=20×440;83=106伏 (13)
为了精确地调整稳定电压的大小,应把计算得到的线圈匝数适当地增加一些,例如10%。绕完线圈后应从338匝和375匝处抽头。
稳压器的调整
为了调整稳压器,按图6所示的电路接线。自耦变压器可以均匀地改变稳压器的输入电压,此电压可由电压表V\(_{1}\)量出。变阻器R1采用电阻为500欧姆或稍大一些的,以使流过电流表A中的电流为1安培。均匀地增加稳压器的输入电压,则由电压表V\(_{2}\)测得的负载电压开始缓缓增大而后停止。这时电压表V1的指示值就是供电网络电压可能脉动的下限。
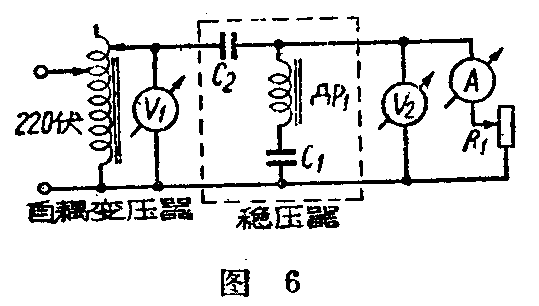
移动变阻器R\(_{1}\)的滑动触头确定额定负荷电流(由前述计算知为0.91安)。
其次增大输入电压到250—300伏,并注意负载电压的变化。当负荷电压的脉动超过给定值时(±0.5%或1.1伏),就需要改变一些C\(_{1}\)值的大小。
如果负载电压的平均值大于或小于220伏,应相应地减少或增加扼流圈线圈的匝数,为此线圈需设有附加抽头。改变C\(_{2}\)的电容量可调整允许的网络电压下限。
为减小稳压器工作时的哼声,铁心的钢片应紧固并灌注绝缘混合剂。(肖进荣根据苏联“无线电”1961年1月号编译)