收音机变频器的设计

变频器是超外差式收音机不可缺少的一部分，变频器的任务是将外来信号的频率变成“中间频率”，简称“中频”或“中周”。收音机中如果没有高频放大器的话，变频器直接与输入回路相连接；它的输出端通过中频变压器接到中放管去。

变频器包括本机振荡器（或称“外差振荡器”）和混频器两部分。一般收音机大多用一个五栅变频管兼作振荡管和混频管。以6A2П为例，它的阴极、第一栅（振荡栅）和第二栅（或称“振荡板极”）组成一个三极管，用以产生振荡；它的阴极、第三栅（信号栅）、第四栅（帘栅）和抑制栅、屏极等各极完成混频的任务。变频器的主要任务就是由本机振荡器产生一个与外来信号频率差一个中频的振荡信号（一般比外来信号高一个中频）；然后把它与外来信号一起送进混频器；混频以后，在变频器输出端得到中频。例如外来信号是1000千赫，本机振荡信号为1465千赫，混频后得到1465—1000=465千赫的中频。

6A2П是常用的外差变频管，采用这一类变频管的本机振荡器多接成如图1，甲那样的电感抽头式振荡电路；但也可以接成像图1，乙那样的电路。

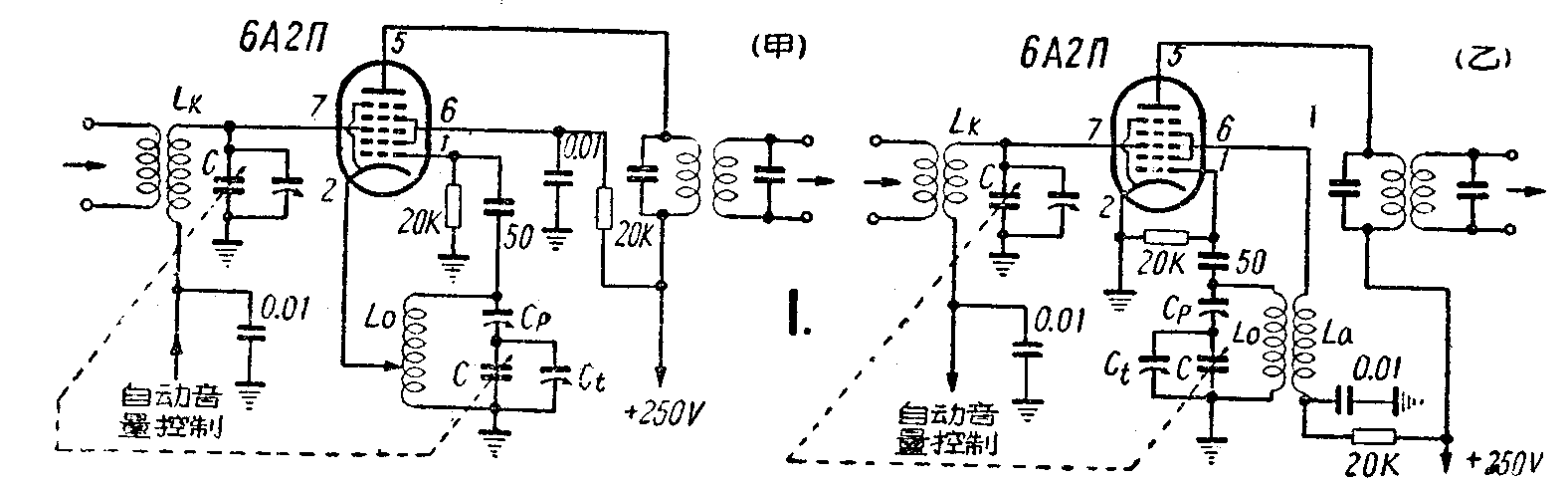
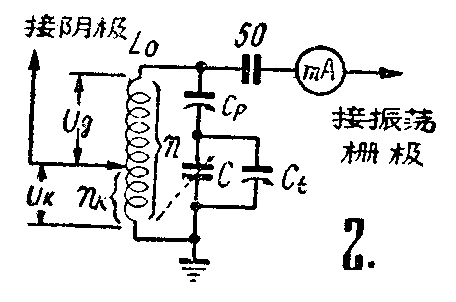
电感抽头式振荡线圈的抽头点，是决定本机振荡工作状态的关键，它对变频器增益的大小影响很大，最好用实验的办法决定。图2中假定抽头到地电压为U\(_{k}\)，抽头到线圈另一端电压，即栅、阴间的振荡电压为Ug，并设振荡线圈L\(_{o}\)的全部圈数为n，抽头点到地一端的圈数为nk，以p表示\(\frac{n}{_{k}}\)n，则

从上式可以看出，抽头往下移，即n\(_{k}\)减少时，Uk减小；反之，抽头往上移，则U\(_{k}\)增大。Uk不宜太大，也不能太小。U\(_{k}\)过大，将使本机振荡过强，容易产生超高频“寄生振荡”，破坏收音机工作，并且当收音机调到不同电台时，本机振荡电压大小不一，从而使收音机灵敏度在接收的波段内不均匀。但Uk过小，本机振荡器容易停振，使收音机不能正常工作。

一般使用五栅变频管6A2П时，振荡电压选在U\(_{k}\)=0.8伏（有效值）左右；Ug选用约10伏比较合适。

以U\(_{k}\)=0.8伏，Ug=10伏代入，将算出p=7.3%，即抽头点应在全部线圈圈数的7.3%左右。实际绕制时都把抽头点抽在7～17%处，其中中波段多用7～10%；短波段用10～17%。

抽头点的选择还与振荡栅流有关。如果抽头点离接地端过远，即n\(_{k}\)过大，则当振荡栅流大时，变频跨导将下降很多，对变频器工作不利。一般6A2П工作在振荡栅流约0.5毫安左右比较合适（图中毫安表指示0.5毫安，或用微安表，则指示500微安）。值得注意的是：振荡栅流与帘栅电压有很大关系，6A2П管正常帘栅电压应当用100伏。

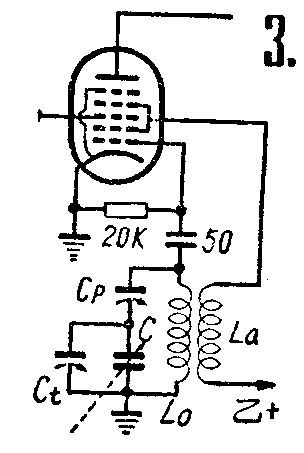
计算电感耦合式振荡线圈（图3）时，主要是要求出回授线圈La，它近似地可根据下式计算：

上式中：k是L\(_{a}\)和Lo之间的交连系数，应该选择得愈大愈好，一般可绕到k=0.6左右；S是振荡管的跨导（毫安/伏）；Q是回路的品质因数；C则为调谐电容（微微法）。

绕制时L\(_{a}\)应多绕几圈，最后用实验法调整圈数使振荡栅流为0.5毫安左右；并使振荡电压在整个波段内均匀，即在波段内转动双速可变电容器时，毫安表表针应不来回摆动为止。

所谓“跟踪问题”，就是要解决超外差式收音机在可变电容器转到任何一个位置时，保证本机振荡的频率减去外来信号频率，都应当等于中频。如果我们就简单地将双连可变电容器的一组接在输入回路，一组接在振荡回路，而不采取特殊的办法，那么就不能达到跟踪的目的。目前多采用“修补”法来解决这个问题。所谓修补法外差跟踪，就是在本机振荡回路中，加入一个串联的电容器C\(_{p}\)（称为“垫衬”电容器）和一个并联的电容器Ct（称为“补偿”电容器），见图4。这两个电容器一般是用半可变的。调整它们到合适的位置，就可以使双连电容器C转动时，能在三点上完全跟踪，也就是电容器有三个位置可以得到准确的中频，而在其它位置时有误差存在。

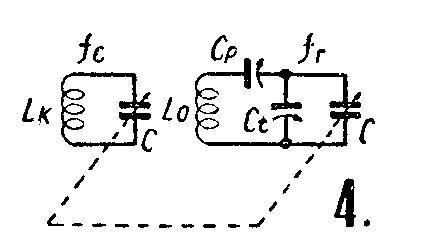
要计算振荡部分各元件，首先应该选定三个准确跟踪的频率f\(_{1}\)、f2、f\(_{3}\)，因为他们选用不同的数值时，所得的跟踪误差是不同的。苏联学者伏·依·西福罗夫所提供的设计方法是比较简单而实用的。用这种方法计算三个频率的公式如下：

式中：f\(_{最大}\)、f最小分别为接收波段的最高频率与最低频率。例如接收535千赫（f\(_{最小}\)）～1605千赫（f最大）范围的中波段，则由上面式子算得：f\(_{2}\)=1070千赫；f1=607千赫；f\(_{a}\)=1533千赫。然后根据f2按图5曲线分别找出m、C\(_{p}\)/C最大及C\(_{t}\)。上例中f2=1070千赫，所以应当在横轴f\(_{2}\)=1070千赫处引一垂线，交三曲线于三点，读得m=0.55，Cp/C\(_{最大}\)=1.16，Ct=10微微法。如果已经计算得输入回路的L\(_{k}\)=240微亨，C最大=369微微法（包括补偿电容、输入电容和分布电容），则：

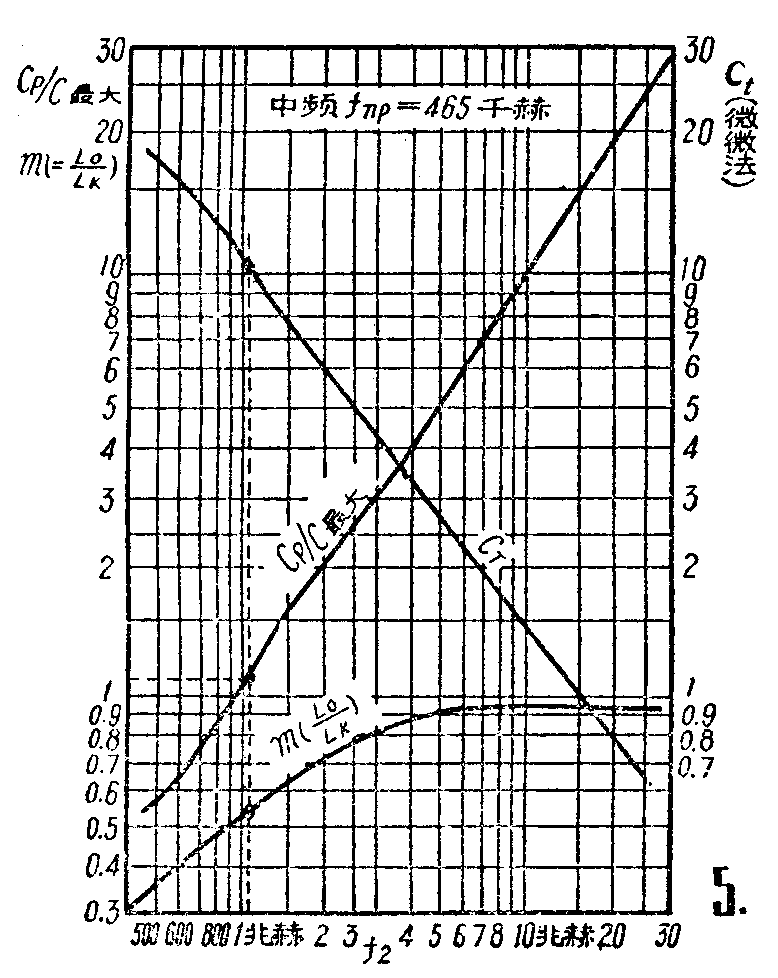
注意图5曲线是按中频为465千赫计算而得的，因此只能用在465千赫的情况下。

算出 L\(_{o}\)、Cp、C\(_{t}\)后，可以采用几种不同方法连接振荡器回路，常见的有图6所示三种。

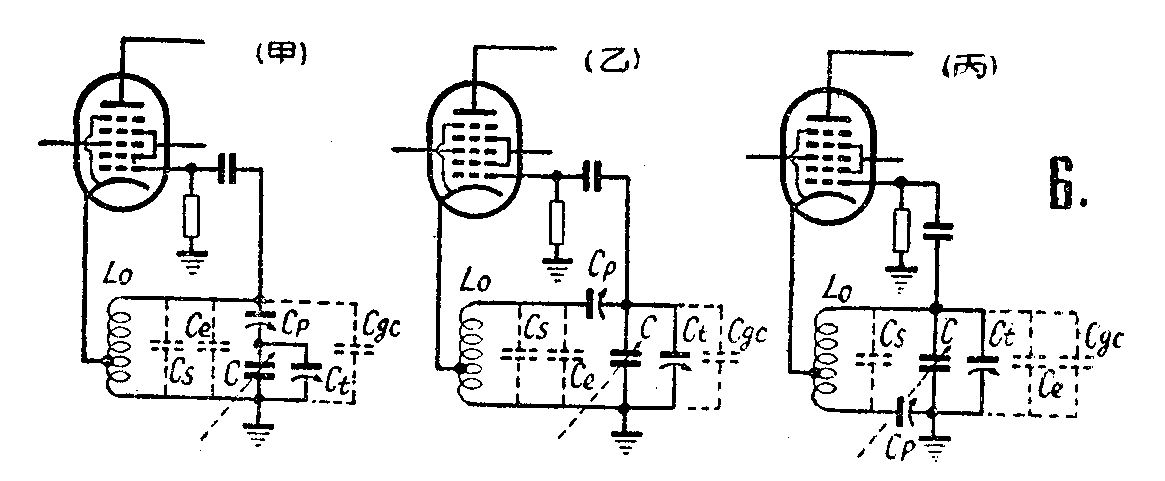
需要指出：根据以上计算，往往与实际要求有出入，因为有些分布电容在计算时没有考虑进去。假定图6中，C\(_{gc}\)代表振荡管输入电容；Cs代表线圈L\(_{o}\)的固有电容；Ce是接线分布电容。在图6，甲的电路中，这三个电容都是并联在线圈L\(_{o}\)的两端，而在上面计算跟踪时全末考虑，它们的影响较大；图6，乙中只有Cgc并联在可变电容器的两端，略略减小C\(_{t}\)，就可消除它的影响，但这时Ce与C\(_{s}\)仍然没有考虑在计算之内，仍有影响；图6，丙那样的接法，Cgc与C\(_{e}\)都并联在可变电容器的两端，不难设法消除它们的影响，只有Cs未加考虑，但C\(_{s}\)究竟是不大的，对上面的计算影响不大，因此图6，丙电路是最接近于理论计算的接法，也便于调整。在多波段的收音机中，调换波段时，是用波段开关换接不同的振荡线圈，为了防止线圈与线圈之间的吸收，往往将所有不工作的振荡线园两端都短路。如采用图6乙和丙的电路时，就不能将线圈彻底短路，因为Lo与C\(_{p}\)组成的回路仍然会产生吸收现象，因此使它们的应用受到一些限制。

变频器组装好以后，最容易发生的故障是产生超高频寄生振荡。这种振荡是超高频的，频率约为100～120兆赫。它是“寄生”在收音机里的，所以叫它“寄生振荡”。变频器带有寄生振荡，它的工作就不会正常：往往会使收音机忽然停止工作，这时若将可变电容器往外转一下，便又能听到声音；有时整个接收波段内有一段的电台收不到。要检查是否存在寄生振荡，最简便的方法是检查振荡栅流，像6A2П这样的五栅管，正常工作时的栅流约为0.5毫安。如果存在超高频寄生振荡，那末振荡栅流会下降到0.1毫安左右；但如果振荡栅流小到10微安左右，那是说明振荡器完全不振，并不说明有寄生振荡。

超高频寄生振荡产生的原因，总的说来是由于零件排列不当，接线过长，以及本机振荡器工作状态选得不恰当所引起的。如果振荡线圈抽头到变频管阴极的接线和振荡栅到振荡回路的接线过长，那末这些接线本身的电感就不能忽略。前一接线的电感约在1微亨以上，后一接线约有0.2微亨的电感。它们与变频管振荡栅极和阴极间电容C\(_{gk}\)（约8微微法）、阴极对地电容Cke（约10微微法），以及振荡板极对地电容C\(_{ae}\)组成振荡回路，引起超高频寄生振荡。

根据经验，振荡管到振荡线圈的接线总长超过15厘米，或振荡管使用高频性能太好的栅漏电阻R\(_{g}\)；或是振荡线圈抽头点太高，振荡太强；以及多波段振荡线圈之间发生吸收现象等，都可能产生超高频寄生振荡。

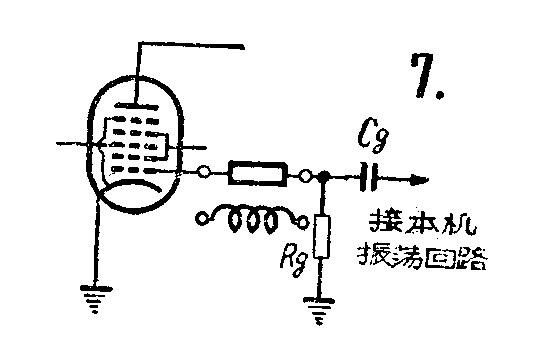
要防止发生超高频寄生振荡，最有效的方法是在振荡栅极电路内紧靠栅极串联一个30～100欧的电阻，或2～3微亨的电感（图7中粗线所示）；或也可以在振荡栅漏电阻R\(_{g}\)的两端并联一个约2微微法的电容器。除此以外，Rg不要用超小型的，最好用1/4W或1/2W的，以增加它对地的分布电容，这样也能阻止寄生振荡的发生。（丁启鸿）