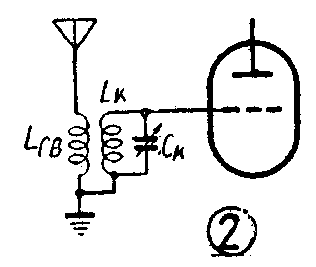
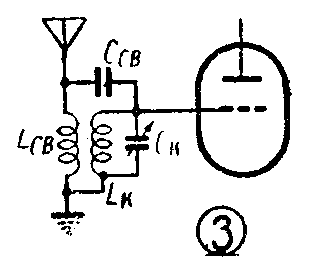
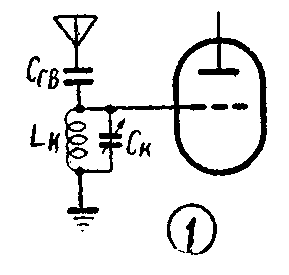收音机的“输入电路”就是介于天线输入端到变频(或高放)管控制栅极之间的电路。它的作用是将信号最大限度地传送到变频管栅极,并且尽可能地扼制干扰。一个设计良好的输入电路应该达到:1.电压传输系数(控制栅极上所获得的电压与天线输入端电压之比)要尽可能的大,并且要求在接收整个频带内各种频率的信号时给出的电压传输系数最好都相等或相差不多;2.有足够的选择性;3.天线参数变化对输入电路的影响最小。
电容耦合式的最大缺点是在整个接收波段内电压传输系数不均匀。电感电容耦合式受天线参数变化的影响较大。最常用的要算电感耦合式输入电路了。这种电路的电指标优良,制作也比较简单。下面就专对这种电路进行分析。
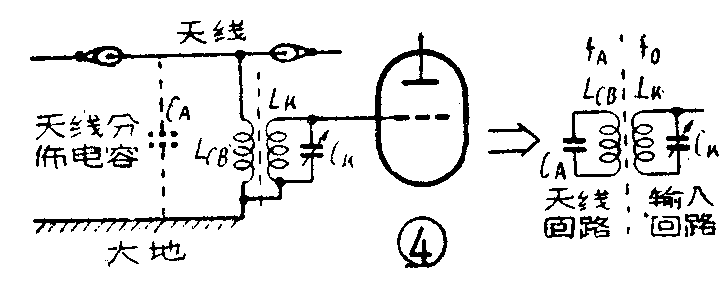
收音机的天线与地之间有分布电容存在(见图4)。这个电容C\(_{A}\)与天线线圈的电感LCB并联,组成了一个谐振回路(图4中虚线左边部分),它的谐振频率f\(_{A}\)为:
f\(_{A}\)=\(\frac{1}{2π}\)\(\sqrt{L}\)CBC\(_{A}\)
天线型式及长度选定后,C\(_{A}\)就固定了, 因此选用不同的LCB,可以得到不同的f\(_{A}\), 这有三种可能性,即:(1)fA低于收音机所接收频带的最低频率f\(_{o}\)最小,称为“高阻抗接收”(或“长天线接收”);(2)fA高于所接收频带的最高频率f\(_{o}\)最大,称为“低阻抗接收”(或“短天线接收”);(3)fA在接收频带之中。因此,这种输入电路有三处设计方案。
第(3)种是最坏的设计方案,因为它在整个接收频带内电压传输系数很不均匀;另外,在天线回路的谐振频率一点上,输入回路L\(_{K}\)CK无法调谐,使选择性和灵敏度都受到影响。因此,这种方式很少有人采用。第(2)种和电容耦合电路的情况差不多,因此也不够理想。目前采用得最多的要算第(l)种高阻抗接收了。
在设计高阻抗接收的输入电路时,首先要确定天线回路的谐振频率f\(_{A}\)应该是多少,其次要确定LCB与L\(_{K}\)采取多大的耦合,也就是决定它们之间的交连系数k,最后决定输入谐振回路的电感LK。
如果把f\(_{A}\)选定在远小于fo最小之处,它的好处是在整个接收频带上,电压传输系数基本上与频率无关,这是我们所希望的;但f\(_{A}\)太低,LCB将太大,以致电压传输系数降低很多,这是不合适的。相反,如果把f\(_{A}\)选得接近fo最小,这时如果接收波段是中波的话,f\(_{A}\)将十分接近中频465千赫,这又可能产生两种恶果:(1)中频很容易发生自振,特别是当电容器转到波段的低频端,而且天线输入电路又接近中频变压器的引线附近时,就会发生呜噜呜噜的叫声;(2)一旦天线换成短天线,也就是CA减小的时候,就有可能使f\(_{A}\)上升到接收频带之内。如上所述,这将使输入调谐回路LKC\(_{K}\)在fA这一频率上失去调谐的可能。图5是实验所得的一些曲线,表示改变L\(_{CB}\)的圈数时,电压传输系数在整个接收频带内的变化情况。从图中可以看出:随着LCB圈数增多,电压传输系数越来越小,但它在整个波段内是比较均匀的,变动很小。当圈数减到100圈时就会使输入调谐回路在590千赫处失调;如减到80、60、40圈时,将分别在680千赫、880千赫、1250千赫处失调。以上的情况都是应用14微亨的电感、150微微法的电容和50欧的电阻所组成的等效天线测得的。如果使用小参数的天线,失调的频率还会升高。实际上收音机往往拖一根一至二米长的线,当作天线,稍不注意就易犯这个毛病。
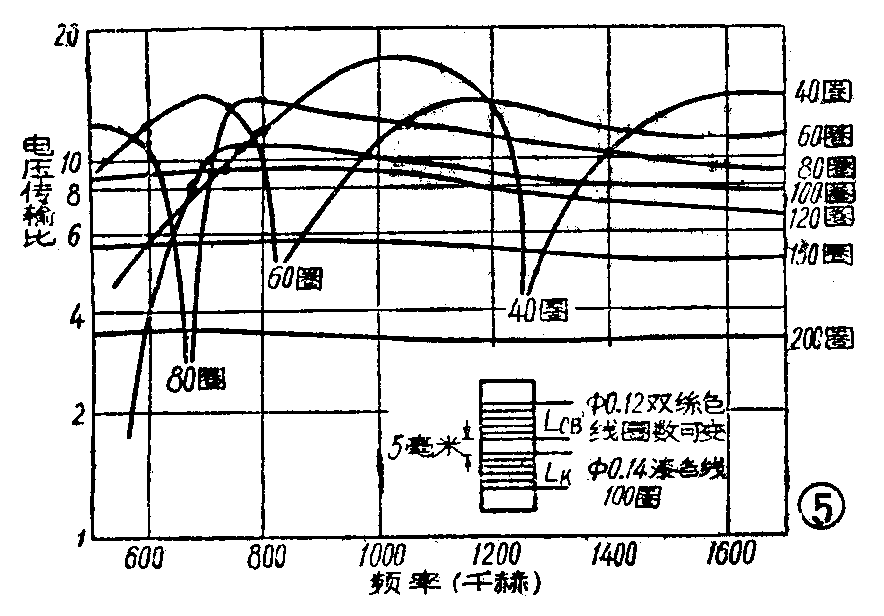
究竟f\(_{A}\)选在什么频率上好呢?经验证明fA=0.7×f\(_{o}\)最小比较稳妥。以接收545~1500千赫的中波段为例,fA最好不要超过0.7×545≈382千赫。决定了f\(_{A}\)以后, 还要估计到今后可能因使用不同天线而引起的天线参数的变化,否则就不好确定LCB的大小。例如我们假定天线参数中的C\(_{A}\),今后可能在150~300°微微法之间变动。那么,应该把注意力放在CA为最小(C\(_{A}\)最小)的情况。因为在这种情况下没问题,CA最大的情况(C\(_{A}\)最大)下就更不会有问题了。这样LCB可根据公式(1)来计算得出:
L\(_{CB}\)=\(\frac{2.53×10}{^{4}}\)CA最小(微微法)f2\(_{A}\)(兆赫)(微亨) (1)
下一步我们来决定交连系数k。k越大,电压传输系数也越大, 但k超过某一极限值以后,k再大,电压传输系数就反而要下降。这个极限值我们叫它作“最佳交连”(或“极限交连”)。所以只要不超过最佳交连,单纯从提高电压传输系数出发,我们应该把交连系数k取得越大越好,但它受下列三个条件的限制,只能适当的选取k值。
1.实际绕制的可能性,例如蜂房式线圈的k值最多只能达到0.5~0.6,而单层管状线圈只能达到0.4~0.5。k值再大,是做不出来的。
2.输入调谐回路的失谐不能超出某一极限数值。大家知道,天线回路的阻抗会对输入调谐回路发生影响。其中电抗分量所造成的影响是使输入调谐回路中产生一个负电感,结果使得L\(_{K}\)减小,因而使调谐频率偏高。偏高的程度不但直接与k的大小有关,还和接收频率fo,以及天线谐振频率f\(_{A}\)有关。因此不管k取多大的值,只要fo、f\(_{A}\)变了,上述负电感(“反射电抗”)也会改变,它不是一个常数。因此不能简单地用加大LK的方法抵消负电感作用来解决问题。这就限制我们不能把k选得太大,否则就会由于失谐太严重,使接收频率越出输入调谐回路的通频带,影响收音机的灵敏度。一般以下列公式来计算k值:
k=2\(\frac{\sqrt{1}}{2}\)δ(1-X\(^{2}\)A\(_{1}\))(1-X2A2);X\(^{2}\)A\(_{1}\)-X2A2(2)
式中δ是输入调谐回路的衰减, 它等于回路Q值的倒数。
X\(_{A1}\)=fA最大f\(_{o}\)XA2=f\(_{A}\)最小;fo
计算的时候我们总是在接收频带的最低频率(f\(_{o}\)最小)上进行,因为在那里通频带最窄,最容易受失谐的影响跑出通频带外面去,因此设计时把公式(2)中的fo换成f\(_{o}\)最小来计算。
3.输入调谐回路的选择性不能低于某一极限值。天线回路的电阻分量也对输入调谐回路发生影响,其结果是降低后者的Q值。采用最佳交连时,虽然可以得到较大的电压传输系数,但此时输入调谐回路的选择性会降低很多,因此也有它不利的一面。一般只允许输入回路的Q值降低20%左右,太多了就不好。因此交连系教k只好选得比最佳交连时的k略小一些。取最佳交连的k值的1/2是合适的,这时可按下列(3)式计算k
k=0.25\(\frac{\sqrt{Q}}{_{A}}\)QK(3)
式中:Q\(_{A}\)为天线回路的Q值(一般取QA=50);
Q\(_{K}\)为输入调谐回路的Q值。
根据以上三个条件设计出三个不同的k值,然后拣其中最小的一个应用。下列经验数据可供大家设计中参考:
中波:535~1500千赫,L\(_{CB}\)=1.3毫亨,k=0.25;
短波:3.94~12.1兆赫,L\(_{CB}\)=4~25微亨,k=0.03。
最后,我们来设计输入调谐回路的线圈L\(_{K}\)。LK与电容 器C\(_{K}\)配合起来,应能调谐于所接收波段的各个频率上。当电容器CK完全旋入时,应能调谐于波段的最低频率f\(_{o}\)最小;完全旋出时,应能调到最高频率fo最大。设计收音机时,要求能接收多宽的波段是预定的。因此可求出“波段复盖系数”k\(_{д}\)(即所接收波段的最高频率与最低频率之比)如下:
k\(_{д}\)=fo最大f\(_{o}\)最小
例如:中波段k\(_{д}\)=\(\frac{1600(千赫)}{500(千赫)}\)=3.08;
短波段k\(_{д}\)=\(\frac{18(兆赫)}{6(兆赫)}\)=3。
第二步要掌握回路可变电容器C\(_{K}\)的最大与最小电容量(CK最大与C\(_{K}\)最小),一般市售可变电容器有一定规格,例如国内常用的一种,动片全部旋出时的最小电容为12微微法,全部旋入时的最大电容量为360微微法。目前12(最小)—498(最大)微微法的另一种新产品使用渐多。知道这两个数据就可以用下式算出LK:
L\(_{K}\)=\(\frac{2.53×10}{^{4}}\)(k2д-1)(C\(_{K最大}\)-CK最小)f\(_{o}\)\(^{2}\)最大(微亨)
上式中:C以微微法计;f以兆赫计。
但是用上式算出的结果还不有符合实际情况,还需要作如下修正;因为C\(_{K}\)的变化与它所引起的调谐回路频率的变化之间并不是直线关系。当L固定时,C与频率的平方成反比,即
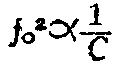
因此,频率从低端到高端如变化三倍(即k\(_{д}\)=3),电容器从最大电容到最小电容必需变化3\(^{2}\)=9倍才能满足要求,但实际上不可能,例如12—498微微法的电容器,它的最大最小电容量之比太大,即有
为了解决这个问题,在C\(_{K}\)上附加一个微调电容器Cд, 例如50微微法(见图6),结果
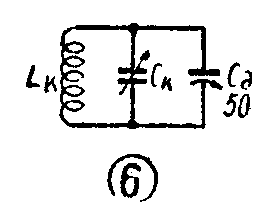
附加电容C\(_{д}\)可按下式计算:
C\(_{д}\)=CK最大-k\(^{2}\)\(_{д}\)CK最小k2\(_{д}\)-1
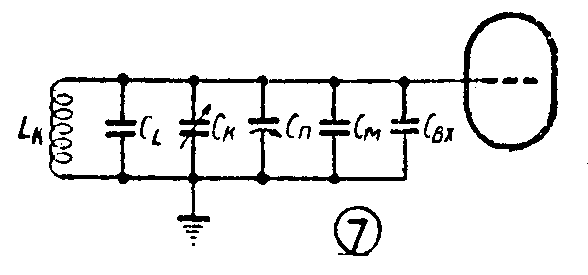
但是,实际上在输入调谐回路中还存在有线圈L\(_{K}\)线匝间的分布电容CL、下级电子管的输入电容C\(_{BX}\)和连接线的分布电容CM(见图7)。计算时应该把它们都考虑进去。因此计算出需要附加的电容C\(_{д}\)后,还应减去这些电容,才是真正应当附加于CK的微调电容C\(_{n}\),即
C\(_{n}\)= Cд—C\(_{L}\)—CM—C\(_{BX}\)。
一般售品线圈中L\(_{K}\)的分布电容CL大约为3.5微微法(分两层绕)或10微微法(绕一层)。C\(_{BX}\)可从电子管手册查到。CM一般靠近底板的接线每5厘米长就有10微微法。接线愈长C\(_{M}\)愈大。(丁启鸿)