为了实现生产过程全盘自动化,必须解决自动控制的复杂问题。随着自动技术的发展,控制定律便越来越复杂。控制跟复杂、迅速、精确和自动的计算有了密切连系。计算机被用来作为自动装置的控制部分。
计算机在自动技术中可以有下列用途。
求解繁复的数学问题 这通常是在计算和设计自动装置中所不可少的。
控制装置的调整 这项工作一定要在由控制装置和被控物体构成的闭合系统中进行。控制装置先跟物体的模型——多半是电子模型相连接。在物理本性和结构方面,模型和实际物体可以相差很多,但是它的输出量值与输入量值间的依从规律是和实际物体一样的,换句话说,它的演算律和物体的相同。控制装置在这样的闭合系统中进行调整,然后把调整好的控制装置装在实际物体上。被控物体的模型不但在调整控制装置时十分有用,而且在设计它的时候也很有用。
电子计算机用作自动装置的控制部分 采用复杂的控制演算律,可以使各自独立的生产过程相互协调起来。例如,在化工企业的个别设备中出现了就某种意义来说,能获得最好的结果(生产率最高,生产过程最快,原料、电力或者燃料最省)的生产过程的可能性。这样,被控设备就能工作在最佳状态。
往往有这样的情况,事先不知道应该怎样控制生产过程,以获得最佳工作状态。有时候设备的特性可能产生预计不到的变化,因此无法事先算出最佳控制演算律,并把它放进控制用的计算机中。在这种比较复杂的情况下,使用具有所谓“自动调整”系统的计算机可以获得所需的结果,自助调整系统象自动实验员那样工作,它对设备进行一系列的试验,分析试验的结果,并找出符合逻辑的结论,控制演算律应该怎样改进,以获得最佳结果。自动调整系统用自动寻找最佳控制演算律的办法,“学会”了控制设备的更好的方法。
目前,自动调整系统还刚开始发展。但已为复杂生产过程的自动化开辟了特别宽广的前景。
电子计算机用来控制生产过程的例子和可能性
目前正在进行寻找电子计算机用于生产自动化的途径的紧张工作。但是这些工作绝大部分还处于用电子模型来设计和研究生产过程或者创制控制装置的雏形的阶段。作为一个例子,我们讲一讲生产中第一批使用的其中一种系统——钢管焊接机的控制系统,它是苏联科学院自动技术和遥控力学研究所研制成功的。这种系统的电路如图1所示。
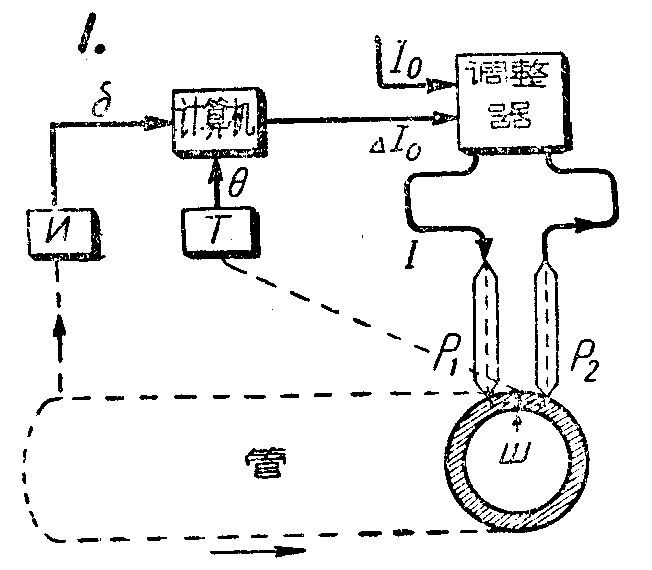
钢板卷成管子,接缝ш用电流I来焊接,电流通过压紧在管子上的滚轮P\(_{1}\)和P2而加到管子上。在焊接过程中使接缝保持一定的温度θ,能获得均匀而质量良好的焊缝。为了使这个温度不变,电流I依靠调节器而保持恒定不变。这个调节器能保证电流I和调节器输入电流I\(_{0}\)相等。但是,温度θ还可能随其它因素:管子的厚度δ、管子表面的特性、金属的性质等等而变化。θ和管子厚度δ的依赖关系最为重要。为了把这个关系考虑迸去,管子的厚度用测量仪表И测定,并将测定的结果送进计算机中去。在计算机的输出端便出现对电流I0的修正电流ΔI\(_{0}\),补偿厚度δ变化的影响。这个修正考虑到从测定δ的瞬间起到测得的δ到达焊接滚轮P1和P\(_{2}\)的滞后时间。
在ΔI\(_{0}\)修正公式里的比例系数k,事先是不知道的。它是在电子计算机本身中用下述方法自动确定的。测量仪表T测定焊缝的温度θ,并把测量的结果送进计算机。后者将δ和θ的读数进行比较,并算出所谓修正函效——δ和θ变化的依从关系。如果这两个量值是互相依从的,那么比例系效k便自动地朝某一个方向变化。如果弄清楚δ和θ的变化没有牵连关系。那么,很明显的,是其它的因素影响θ的变化,而不是δ。在这种情况下,比例系数的大小保持不变。
设备的运转表明:与普通的调节电流I的装置相比,温度θ的波动减小为原来的\(\frac{1}{8}\)到1;10。
控制炼钢电炉的电子计算机可以作为另一个例子。计算机补足加进电炉的电功率,即以紧跟着的增大功率来补偿功率的偶然减小(或者反过来以紧跟着的减小功率来补偿功率的偶然增加),使得在一定的时间内往电炉里加进严格控制的一定的能量。结果,炼钢过程的结果随每炉而变化的幅度减小。这时,正如运转所表明的,炼钢时间缩短20%。
自动最佳系统是自动调整系统的一种,它能自动地找出某一量值的最大值或者最小值。这种系统的最简单的形式是极大系统,它能自动找出参量x的函数y的最大值(图2)。
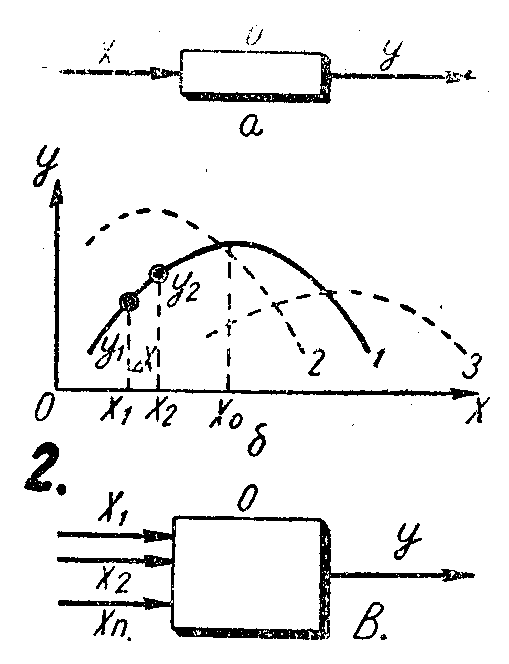
假定可以找出柴油机的最大功率或者效率与单位时间内输入的燃料或者空气间的关系。在电炉里,可以找出其中发出的电功率与电极的电流间的关系。在图2.a中,设备的输入端以字母x表示,而输出端以字母y表示。要求自动选定这样的量值x,使输出量值y为最大。
如果y对x的依从关系是始终一样的(见图2.6中的实线),那末一下子便能选定这样的数值,即x=x\(_{0}\) ,这时y为最大。但是,假定曲线y=y(x)慢慢地作不能预见的变化。例如,曲线可以占据曲线2或者3的位置(见图2.6)。在这些条件下,需要自动寻觅最大值。计算机控制设备的演算律应该这样来编制。设在最初的瞬间x=x1,最大系统进行试探动作,将x增大量值Δx。现在量值x变得等于x\(_{2}\)=x1+Δx。这时测定y\(_{1}\)和y2的数值。如果y\(_{2}\)-y1>O,那么很明显的,应该继继续增大x。如果y\(_{2}\)-y1<O,那末应该减小x的数值。工作动作结束后,重新进行试探动作。最后,x的数值移到相应于y最大值的顶点。
如果设备0的输出量值y跟几个输入量值x\(_{1}\)、x2……x\(_{n}\)(见图 2.B)有关,那么演算律便复杂了。在这个情况下,必须对每一个变量xn进行事先试探动作,以便弄清楚它们应该朝什么方向变化才能接近最大值y。试探动作结束后,进行工作动作,以后再是试探动作等等。这种演算律也是在计算机中实现的。基于这一原理的例如控制化学设备的系统,可以自动改变湿度、压力、送料,总之一系列的输入参量,以便获得最大生产率或者产品的最佳质量,或者单位产品的最低成本。这时,常常要求遵守附加的条件,例如,蒸汽的消耗不能超出一定的限度,副产品的质量应该在一定的范围内等等。控制化学设备的计算机,在自动寻觅主要输出量值的最大值时,也可以考虑这些附加条件。
目前,这种装置已由苏联科学院自动技术和遥控力学研究所研制成功,并在实验室的条件下进行试验。
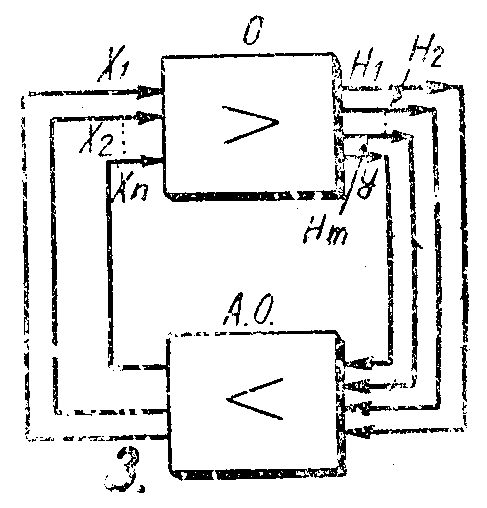
图3示出自动系统的方框图,其中包括控制设备O和自动最佳器A.O。后者自动地改变设备的输入量值——变量x\(_{1}\)、x2、…x\(_{n}\)。在设备的输出端测量要达到最大值的(或者最小值,看需要而定)量值y,以及一系列的量值H1、H\(_{2}\)…Hn,它们不应该超出某一允许范围。
自动最佳器既可以用来加快计算和使计算自动化(例如,用电子模型选择控制部分的最佳参量,控制部分的自动合成),也可以用来控制设备。如果对设备本身不能进行试探动作,会扰乱它的工作状态,那末可以在设备的电子模型上进行试探动作,并将求出的变量x\(_{1}\)…xn的数值送到实际设备上去。
因此,目前存在着使十分复杂的过程自动化的条件。然而,认为在自动化的道路上存在着严重的困难将是错误。为了实现复杂的自动化,必须克服一系列十分严重的障碍:如测量仪表不够好,机械化的水平不够,设备和工艺过程对于自动化来说不太适宜。现代的电子计算机在生产条件下的可靠性还不够等。但在设计应用晶体管、磁性元件和其它元件制成的更可靠的计算机中所获得的巨大成就,使我们能期待计算机的可靠性在最近的时间内不会再成为自动化中的严重障碍。
其他如自动控制的理论发展得不够,也是障碍之一,尽管近年来计算技术取得了巨大的成就,但是在一系列的情况下,理论还不能指出怎祥编制最佳控制演算律,怎样综合由给定演算律控制的比较简单和足够正确的工作系统。今天,理论在许多情况下,是自动化发展中的薄弱环节,在理论方面还有许许多多要做。(朱邦俊摘译 (苏联)A.费尔德巴乌姆)