由于江苏各地田头广播和钢铁基地的需要,成品高音喇叭供不应求,成本也太高。我们试验用簧舌式喇叭当作高音喇叭。当给与一瓦电力时,(1000周计算,阻抗10000欧,电压100伏)在50公尺长,30公尺阔的面积上,可以听得很清楚很响。簧舌喇叭承受2瓦电力时,仍能很好工作,不会损坏。全部成本只要11元(包括人工)。
为了制造简易和不减低线路传输效率起见。没有采用减少簧舌喇叭绕线圈数,降低喇叭阻抗的办法来增加电力。而是原来簧舌喇叭完全不改动,提高输入电压。由于加了木制喇叭筒,喇叭筒起着“声”的变压器作用。对于纸盒来说,声的阻抗提高了,虽然提高了电压,但簧舌的振幅没有显著加大,不会碰两边磁铁,所以仍能很好使用。为了防止低频振幅过大和保护纸盆,喇叭线圈上串联了一只0.1微法电容器。经过试验,纸盆的机械强度没有问题,漆包线的载流量也是毫无问题的。
喇叭筒是方形的,全部用木制,主要材料是三夹板,尺寸见图1。按照这种尺寸,2张三夹板可制3只喇叭筒,如果裁板时很好地排列,可制3只半喇叭筒。
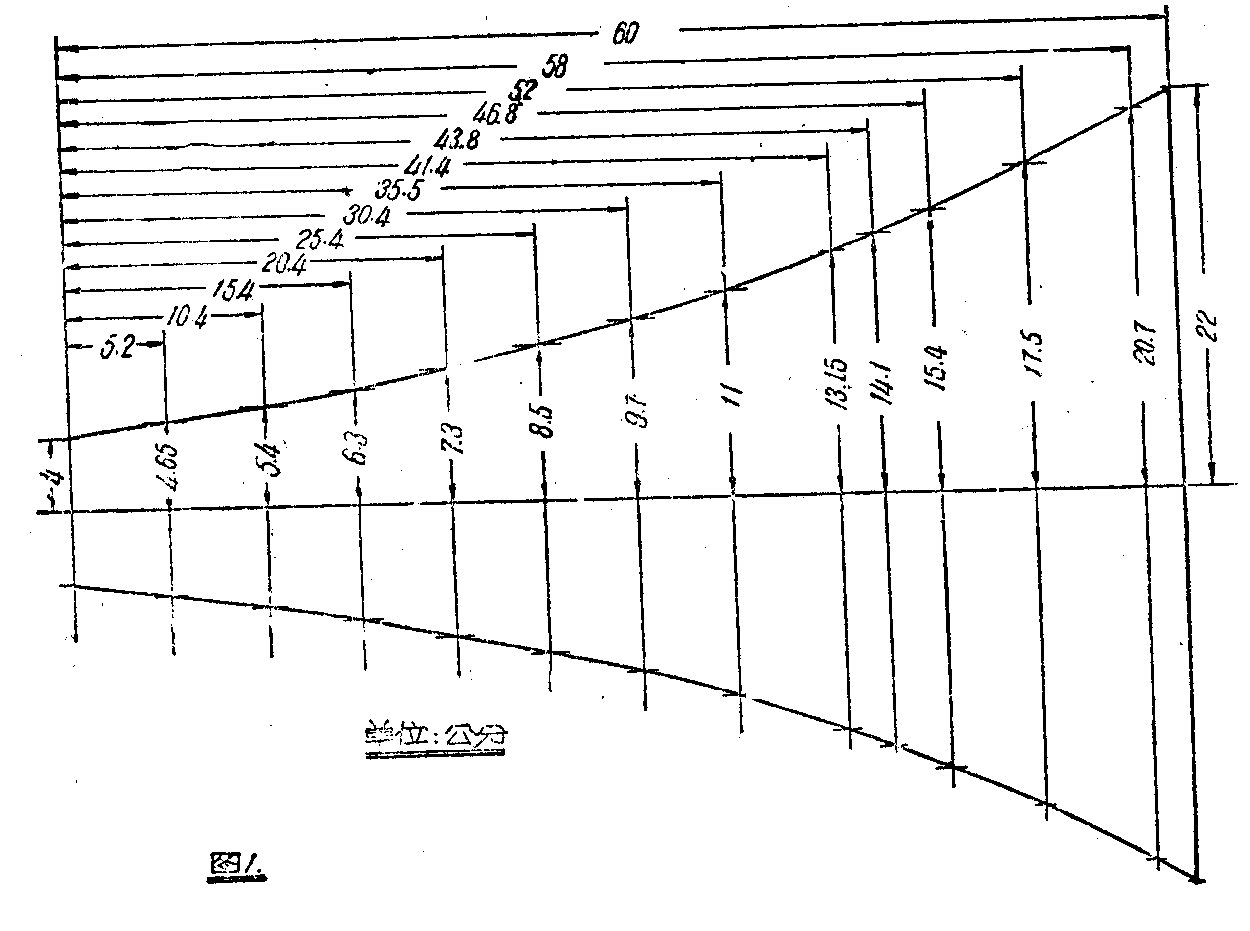
喇叭筒的后部系一只密闭的扁方形普通喇叭木箱,24公分见方,高14公分,前面开八公分见方的洞口,喇叭放在正中央。喇叭筒的边缘均有小木条加固,小木条阔2公分,厚0.8公分,锯成与三夹板边缘一样的形状,钉好在每片三夹板上,然后再合拢。三夹板曲边的形状要求准确(木工的加工工艺,可根据情况由木工自己确定)。
一般的设计方法如下(见图2):
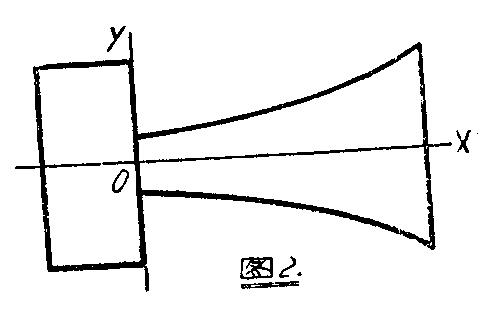
距原点O的距离x与喇叭筒的截面积关系由下式决定:
S\(_{x}\)=SOe\(^{mx}\)……(1)
式中S\(_{x}\)是x点的截面积,单位平方公尺;SO是在原点的截面积,就是筒子喉部的面积;e=2.718,m是一个常数,它决定筒子口部张开的快慢,我们试制的筒子取m=6。
喇叭筒本身是个带通装置,只能通过一定的频带,最低可通频率由下式决定:
f\(_{c}\)=\(\frac{mc}{4π}\)……(2)
式中c是声速,每秒340公尺,π=3.14,f\(_{c}\)是最低可用频率,(2)式是由无限长的筒子推导出来的,实际的喇叭筒子很短,因此实际最低可用频率f′约为fc的1.2倍,即
f′=1.2f\(_{c}\)………(3)
取m=6时,最低可通频率约为160周,实际最低可用频率约为180周,已经能满足要求了。
一般方形喇叭筒口部的周长至少应与最低频率的波长相等,即每边长度不少于波长的1/4。在200周时声的波长约1.7公尺,应采用44分分的长度。上例每边就用44公分的长度。实际测听结果,多数人都认为这种土高音喇叭比未加筒子的簧舌喇叭低音和高音都显著地有了改进。
由于所裁三夹板要向外弯曲,因此实际长度L总是长于(1)式中的x。板的宽度2y以及L与x的关系是:
S\(_{x}\)=(2y)\(^{2}\)=SOemx,
y=\(\sqrt{S}\)\(_{O}\)2e\(^{mx;2}\)……(4)
经过数学推导,裁板长度
L=\(\frac{2}{m}\)[U+1.1513log\(_{1}\)0(U-1;U+1)]-\(\frac{2}{m}\)[V+1.1513log10(V-1;V+1)]…(5);
其中U=\(\sqrt{1}\)+\(\frac{m}{^{2}}\)S\(_{O}\)16emx,
V=\(\sqrt{1}\)+\(\frac{m}{^{2}}\)S\(_{O}\)16。
利用(4)(5)式,把x看作参数,就可以求出所有y和L的对应值。(方锡)