看了本刊1957年第2期“一种消除交流哼声的线路”一文,原作者在说明可用平衡电桥方法来减小交流哼声的分析中所列出的电桥线路,没有考虑电压放大管1/2 6H9C的内阻对电桥平衡的影响。实际上,三极管的内阻较小,一般在数万欧范围内,如1/26H9C的内阻为44千欧,6SQ7为91千欧,与原图C\(_{1}\)—R4—R\(_{5}\)并联后,因R4为末级6Π6C栅极上的耦合电阻,一般为500千欧左右,显见三极管的内阻远较C\(_{1}\)—R4—R\(_{5}\)的阻抗为小。这样,三极管的内阻不能忽略不计,否则计算出来的C1数值将不准确。虽然可以用反复试验R\(_{1}\)C1C\(_{2}\)的数值的办法来实现平衡条件,但究竟不如先计算出一个初步数值,然后来调节R1C\(_{1}\)C2 的数值省时间。
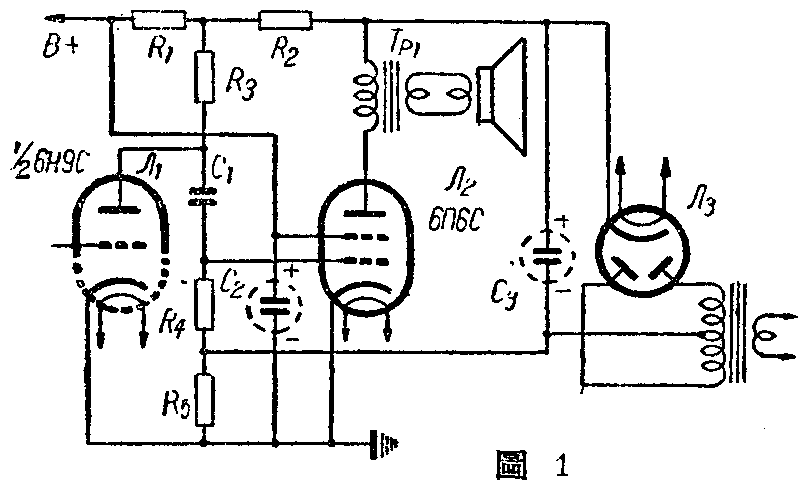
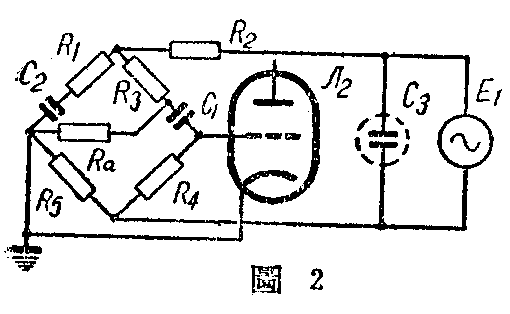
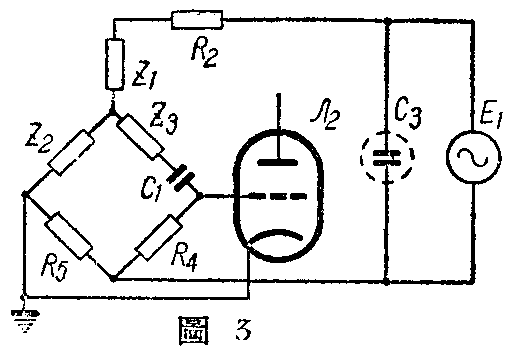
为了说明在分析中不能忽略电压放大管的内阻,将原文的线路重新列出如图1。设在整流管输出端的交流哼声电压为E\(_{1}\) ,1/2 6H9C的内阻为Ra,则电桥电路应如图2所示。我们晓得△形的网路可换成Y形的等效网路,则电桥中的线路经△-Y变换后得图3所示的线路,图中的阻抗:
Z\(_{1}\)=R3(R\(_{1}\)-Xc2)Z,Z\(_{2}\)=Ra(R\(_{1}\)-Xc2);Z,Z\(_{3}\)=R3R\(_{a}\)Z,
Z=R\(_{1}\)+R3+R\(_{a}\)-Xc2.
只有当线路换成图3的等效线路后,才能求出平衡条件,图3的平衡条件为:
R\(_{4}\):R5=Z\(_{2}\):Z3-Xc\(_{1}\).可求得
R\(_{1}\)=R5R\(_{4}\)R3,C\(_{1}\)=C2R\(_{5}\);R4(1+\(\frac{R}{_{3}}\)Ra).
由此可知,电阻R\(_{1}\)的数值与三极管的内阻无关,但电容C1的数值与电压放大管的内阻有关,如不考虑л\(_{1}\)内阻的影响,则C1=C\(_{2}\)R5R\(_{4}\),两者相差R3;R\(_{a}\)=R5R\(_{4}\)C2。根据原文图中数据,R\(_{4}\)=470千欧,R5=220欧,R\(_{3}\)=270千欧,C2=16微法,在考虑I\(_{1}\)内阻的影响时,用1;26H9C作电压放大管,其内阻为44千欧,则取得真正平衡条件时的C1为0.05微法,用6SQ7时,其内阻为91千欧,C\(_{1}\)则为0.03微法左右。如果不考虑电压放大管内阻的影响,则无论所用的电子管的特性如何,所得出的C1皆为0.0075微法,不但得不到减小交流哼声的效果,而且和需用的数值相差过远,调节数值时会使试验调节时间增加。(黄长权)