很多人都认为超外差式五灯机线路很简单易懂,事实上困难问题是很多的,愈深入研究就会发现不了解的问题愈多。其中本地振荡级就是一例。当收音机突然不能收音,为了找寻故障,我们常会感到很苦闷,这种现象经多次试验,它的原因及解决方法,似已得到结论,现介绍如下,同时何种线路该用怎么样的零件也可迎刃而解了。
首先得谈一谈本地振荡级有了故障时有些什么象征。一只工作得很正常的收音机突然不响了,将度盘向高频方面转一下,再转回到原来的度数,又继续响了;或者新装收音机随便怎样调节,度盘—部分总收不到音,当转开收音时开始振荡困难等等情况,都是本地振荡级有故障或停止振荡的原故。可是本地振荡完全停止的情况是很少的,一般是所需的报荡频率停止了,却代之以超高频(VHF)振荡,这可从栅流值来证明。当用20,000欧栅漏电阻发生超高振荡时,约有100-200微安的栅流,但在完全停止振荡时,栅流将降至10微安左右。
数年前电力事业情况较差,电源电压很不稳定,要使振荡良好是很困难的。当变频管6WC5或6BE6等不良,亦会停止振荡,这时栅流将在10微安左右,表示完全停止振荡。
本地振荡的频率,决定于振荡线圈及可变电容器的数值。当振荡级的基本频率振荡减弱时,超高频振荡就开始了。也就是说像6BE6管采用阴极抽头的振荡回路时,有超高频(由接线长度等决定)和基本频率(由线圈和电容器决定)两种振荡的可能。在基本频率受到抽头的影响,或电能被其他零件所吸收,因而振荡减弱时,超高频振荡即代之而起,结果基本频率振荡被迫完全停止。
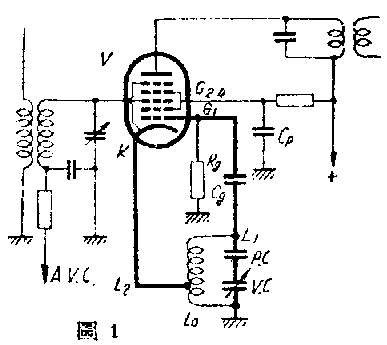
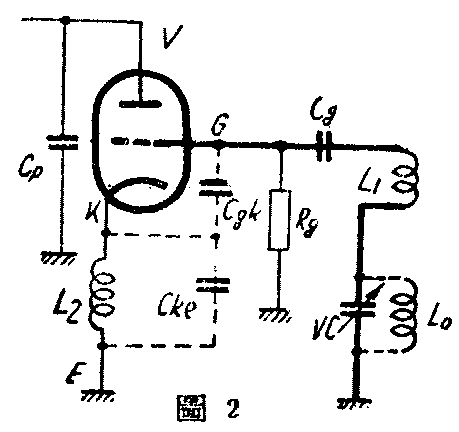
阴极抽头式振荡回路为什么会发生超高频振荡呢?参看第1图,这是一般常用的变频回路,电子管为6WC5或6BE6(这两种电子管相当于我国的产品6A2Л—编者),阴极接于振荡线圈L\(_{0}\)的抽头上,粗线部分形成了超高频振荡回路。在普通情况下,线圈L0,可变电容器VC及垫整电容器PC所组成的回路产生所要求的振荡频率,可是将粗线部分考虑一下,可得到第2图的等效电路,实际在第1图中如仅考虑超高频,可说与第2图是完全一样的。自第一栅G\(_{1}\)起通过Cg、PC、VC至地为止的接线的自感量,约在0.2微亨左右,相当于第2图中的L\(_{1}\),L0 对超高频来说感抗可视作无限大,故不画在第2图中。阴极K接于L\(_{0}\) 的抽头上,对超高频也有1微亨以上的自感量,第2图用L2表示。G\(_{1}\)及Cg部分的线路,即使与底盘远离,仍有1~2微微法的潜布电容量。电子管内G\(_{1}\)与阴极的电容量Cgk约为8微微法,阴极与地的电容量C\(_{ke}\)在灯丝加热状态下约有10微微法。Cgk与C\(_{ke}\)所构成的串联回路,在第2图中以虚线表示。这部分如加以电压,则G点及E点的相位恰相反,中点的阴极在两者之间,与G点、E点各相并90°。这种情形与阴极接在L1的中间抽头上一样,成为哈脱莱式振荡回路,振汤频率由C\(_{gk}\)、Cke及L\(_{1}\)决定。PC及VC的串联回路,在第2图中仅以VC表示,对超高频来说,因Ll与它串联,等于一端接地,所以即使VC容量从最大变至最小,对振荡频率的影响仍然很小约在100-120兆周之间变化,正好落入电视波道中,故常使电视接收机遭受差频干扰。
在实际情况下,超高频振荡常由下列原因引起:
(1)G\(_{1}\)与K至振荡线圈接线长度超过15—20公分。
(2)R\(_{g}\)采用了高频用电阻。
(3)由于L\(_{0}\)的阴极抽头向接地端降低时,易于停止振荡;向上移时,又使灵敏度降低,所以在不引赶超高频振荡的原则下,抽头愈低愈好,以便得到良好的灵敏度。
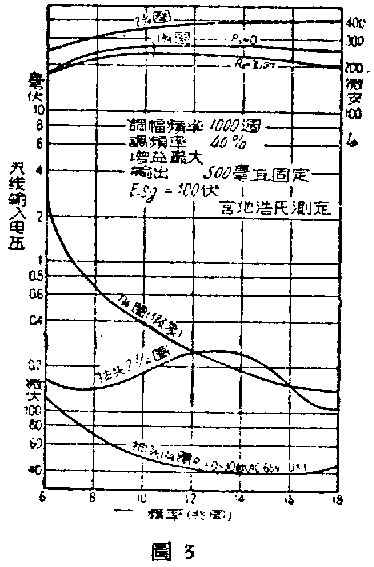
第3图为短波段振荡线圈在2\(\frac{3}{4}\)圈及13;4圈处抽头时,在额定输出功率下所需无线输入电压的关系曲线。由图可知降低抽头一圈平均约可增加灵敏度10分贝.可是在普通状态下(图1的回路),在1\(\frac{3}{4}\)圈处抽头时,不易振荡或振荡很不稳定,但加接下面将谈到的R\(_{s}\)后,常可使振荡良好,灵敏度优越。
以往为了要避免本地振荡停止,常将抽头过份提高,因而只能眼看着灵敏度减低。在明了停止振荡的原因及其对策后,那末就可降低抽头以提高灵敏度了。
在广播及短波段线圈绕在同一线圈管上的所谓单线圈线路里,广播段的线圈常吸收短波振荡电能。当吸收较强时。就发生停止振荡现象。
在有超高频振荡时,栅流约为100—200微安;在正常状态下,栅流则为200—400微安左右。故当本地振荡停止,同时栅流突变为100微安左右,就知道已有超高频振荡发生了。
由于超高频振荡是在第2图中的C\(_{gk}\)、Cke及L\(_{1}\)的串联回路内发生,所见在这部分回路内串联一小阻值的电阻即可制止超高频发生。插入电阻的地方,以CgkC\(_{g}\)之间较为适宜,亦可接于Cg与L\(_{0}\)、PC的连接点之间。第4图中的Rs即为这加入的电阻。在R\(_{s}\)之外也可以再串接一个2—3微亨的扼流圈,使超高频振荡停止,但串联扼流圈易于引起其他频率的振荡,所以还是串联电阻较好。另一个办法是在电子管V的栅极与地之间,加接一小电容器Cs(图4)。当C\(_{s}\)的容量大于Cgk与C\(_{ke}\)。的串联容量时,阴极上的电压低落,超高频振荡因而停止。Cs的容量约在5微微法左右。应孩注意,C\(_{s}\)的容量过大,将使高频端的振荡频率不能产生。
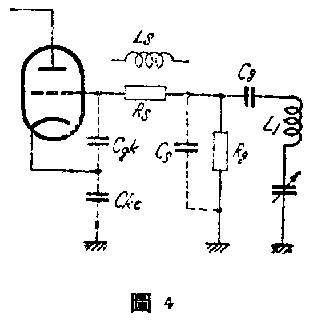
在采用R\(_{s}\)、Ls和C\(_{s}\)之后,对于L0的振荡和频率又有些什么影响呢?因为R\(_{s}\)串联在超高频振荡回路内,而本地振荡的频率却决定于L0、PC和VC之值,栅极G上只有栅压而无显著的栅流通过,而R\(_{s}\)的阻值又只有100欧左右,故对振荡及频率,可以说几乎没有影响。虽然用Ls的情况与R\(_{s}\)相同,但在短波段因频率较高,受Ls的影响常致“追踪”(在同轴调谐中,要求信号调谐回路与振荡回路,经常保持—定频差)困难。当加接C\(_{s}\)时,相当于G和E间的潜布电容量增加,对振荡频率没有很大影响,只要注意把Cs接在靠近G的一端。
其次再考虑一下,如以电容较大的R\(_{g}\)代替Cs又怎样呢?在一般情况下,R\(_{g}\)是用普通\(\frac{1}{4}\)瓦的电阻,约有1一2微微法的电容量,已能防止超高频的发生,在用了高频型的电阻时,大多将发生超高频振荡,这时只要将此电阻换以普通型即能免除。但当普通1;4瓦电阻仍不能完全解决问题时,换用1瓦的电阻后常能达到防止高频振荡的目的。采用1瓦电阻的原因并非在于它的载流量较大,而主要是利用它的并联电容量。在加接30-100欧的Rs后,R\(_{g}\)即使用高频型或普通\(\frac{1}{4}\)瓦的电阻阻,也不致发生故障。在用普通型电阻作Rg时,如将接地端接于阴极,因它与C\(_{kg}\)并联,不但不能制止超高频振荡,反而有增强的趋势。以前常有人将Rg的接地端随便接于阴极或地,在接于阴极时就易发生高频振荡而使本地振荡停止,所以R\(_{g}\)必须注意接在G及E之间,有时接线的潜布电容量很小,电子管的跨导相当大,L0的抽头又低……,在这些情况下,超高频振荡(寄生振荡)发生的机会是太多了,要防止它发生,那就非加接R\(_{s}\)不可。也许有人会想到在振荡回路里加接一电阻,会不会增大线路的损失呢?我们试将前文再研究一下,就会认识到Rs与振荡回路是完全没有影响的。
再谈一下关于C\(_{g}\)的问题。Cg是将振荡电压导向栅极的交连电容器,由于在栅极及地间接有R\(_{g}\),故栅流通过Rg时就产生了负电压,C\(_{g}\)一方面接受这电压充电,另方面防止这电压通过L0而短路。C\(_{g}\)的数值不能很随便,太小了那末加到栅极的电压就降低了,因为输送到栅极的电压是Cg与C\(_{gk}\)的比例而定,当Cg= C\(_{gk}\)时,栅板电压将为振荡电压的\(\frac{1}{2}\)。究竟多少电压才能维持振荡,完全由振荡回路的各项条件决定。根据作者实验,Cg=25微微法时振荡已很良好,在10微微法以下时,振荡停止。因而C\(_{g}\)太小,会造成停止振荡的结果。其次,当Cg过大,超过250微微法时,亦不能得到良好的结果,因为由R\(_{g}\)所生负压使Cg充电,当C\(_{g}\)增大时,负压也就增高,当负压过高时振荡就停止了。振荡停止后Cg经R\(_{g}\)而放电,电压逐渐低落,于是振荡又重行开始,就这样周而复始,形成了间歇振荡。在可变电容器转出的位子,频率较高的部分,振荡回路的Q值较大,因而振荡电压亦较高,间歇振荡更易发生。在短波段Rg用20,000欧时,C\(_{g}\)不能超过100微微法。当发生间歇振荡时,有很强的“轧轧”声可听到。如果Rg=20,000欧,C\(_{g}\)=100微微法而仍发生间歇振荡,那是因为本地振荡太强,须将阴极抽头降低,并减低振荡管电压来解决。如图1的线路,帘栅电压不能超过100伏。本地振荡的好坏并不仅限于振荡强弱一项来决定的。((日本)藤卷安次)(李秉衡,金庚年译自日文“无线电及音响”杂志 1957年6月份)