(张应中)整流器输出的电压不是纯粹直流,它的波形包含有很多谐波。因为这种电压波动是波纹式的,故常用波纹因数来表示它的波动特性。所谓波纹因数就是全部交流成份的电压有效值与平均值的比。
在实用上,整流器输出电压的波纹因数必须由滤波器装置减至极低,以合需要。如在发信机微音器电路的整流器,波纹因数应减至0.0005,如用分贝表示则称为波纹衰减,电压比为0.0005时即衰减66分贝。在音频放大器及收信机,约应为0.0001至0.001,即波纹衰减约应为80分贝至60分贝。在阴极射线示波器的电子注电源则约应为0.01,即波纹衰减约为40分贝。平常要知道滤波器对电压波纹的衰减多少,必需经过计算,手续较繁,这里介绍一种利用图表来查出波纹衰减的办法。
这种图表加封3左图,它适用于扼流圈输入式滤波器,图中横轴代表波纹损耗分贝值,纵轴表示滤波器的电感量L和电容量C的乘积,图中的曲线适用于单相或三相50周的交流电源。整流器则可以是半波也可以是全波整流。图中右下角还列出了整流器本身对波纹的衰减值。利用这种图表可以很快将扼流圈输入式滤波器的波纹衰减值求出。
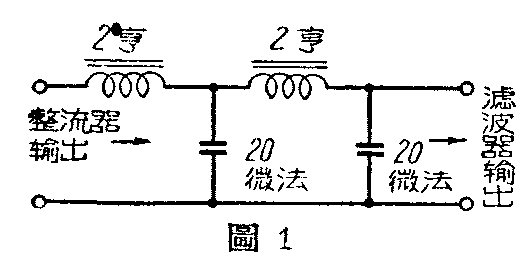
用此图表时,必须要先知道滤波器中的电感量(单位是亨)和电容量(单位是微法),然后算出两者的乘积,求出这一节的衰减数值。如果有几节滤波器,那就分几次求出后再加起来。例如:有一单相全波整流器,用两节扼流圈输入式滤波器如图1,每节滤波器的扼流圈电感量为2亨,电容器为20微法。从第一节滤波器,其LC乘积为2×20=40,从图中曲线可查出波纹衰减为24分贝(或为波纹因数0.0631)。第二节滤波器LC乘积也是40,波纹衰减也是24分贝。再从图中右下角查得单相全波整流器的等量波纹衰减值为+6.5分贝(或是波纹因数0.473)。总的波纹衰减值为上述三者之和,即24+24+6.5=54.5分贝。以波纹因数表示,则为三者相乘。0.0631×0.0631×0.473=0.00188。
上面说的是扼流圈输入式滤波器波纹衰减的求法,这种滤波器多用在需要电压调节度较佳及负荷较大的电源设备上,至于一般收音机,由于负荷较小,多采用如图3的电容器输入式的滤波器,这种滤波器输出的直流电压较扼流圈输入式的为高,但电压调节度则较差。
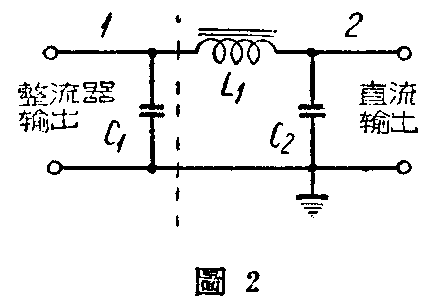
计算这种滤波器的波纹衰减时,可如图2虚线所画分成两部分来计算,第二部分即等于前述的一节扼流圈输入式滤波器。求第一部分的波纹衰减值时,可应用封3右图的曲线,图中曲线的横轴为电容量(微法),纵轴为波纹衰减因数或分贝值,由于电容器输入式滤波器的波纹衰减与负荷电阻值有关,因此图中画出了各种不同负荷电阻值的曲线,正确计算时,还要考虑滤波器的输入电阻。但在一般收音机的滤波器其输入电阻差别不大,且输入电阻对波纹裒减虽有影响但并不大,应用图解已足实用,在10%以下时相当准确,超过10%时则为近似值。此外封3右图的曲线适用于电源频率为50周全波整流,若要用于其他频率则应将电容量按下述数值乘之:
用于25周时乘2,用于40周时乘1.25,用于 60周时乘0.83,用于半波整流时乘2。
利用封3右图时要先知道电容器的容量和滤波器的负荷电阻数值(负荷电阻应包括扼流圈的电阻),其值可用下式求出:
负荷电阻=\(\frac{输出的下流电压}{输出的直流电流}\)(电容器输出)
例:如图2C\(_{1}\)=4微法C2=8微法,L\(_{1}\)=20亨,负荷电阻(包括扼流圈的电阻)=500O欧,电源频率为50周,全波整流,求波纹衰减值。
先由图中的横轴4微法处,按RL=5000欧的曲线,查得波纹衰减百分数约为11.7%,或为19分贝,然后算出L×C=8×20=160,按封3左图查出波纹衰减约为1.58%或为36分贝,再查得单相全波整流器的等效波纹衰减为47.3%或为6.5分贝,故求得总波纹衰减为:
19+36+6.5 =61.5分贝。
或用波纹因数表之为
0.117×0.0158×0.473=0.00087。