在试验工作中往往要特别精确地测量线圈的自电容量。不幸,当使用一般方法时,想得出结果常常并不是一个简单的过程。同时,通常需要几组读数,这样,校准及读出数字时的错误难免比较大。通常决定电感器或线圈自电容量的典型方法是查出电感器分次并联两个不同值的电容量时的谐振频率。根据所得的两个数据算出自电容量。这个方法,除了别的一些东西外,在于精确地决定电容器的谐振频率。当自电容量低时,频率校准的微小误差将引起最后计算结果的极大误差。
这里介绍的线路是一种测量电感器自电容量的新方法,它的好处是对频率不必作准确的校准,因为加到电感器上的频率仅是谐振频率的基本波及其二次谐波,在计算中已经把它去除。这个方法的另一好处是可以得到被测线圈的自电容量和测量用可变电容器间的一个简单的数学关系。假如可变电容器的容量未曾校准过,可以用一般的电桥方法决定。最后,采用这种方法在校验时,不需要知道线圈的真实电感量。
基本原理
图1是测量自电容量的线路接法。信号发生器的输出耦合到被测的线圈,并连接一个电子管电压表。信号发生器及电子管电压表连接的分布电容量图中用C\(_{S}\)表明(实际上CS可以保持一个很低的值)。线圈的自电容量用C\(_{L}\)表示。可变电容器CV可以经过开关连接到线圈的两端。电子管电压表是只需作一峰值指示,用来指示线圈的谐振状况。
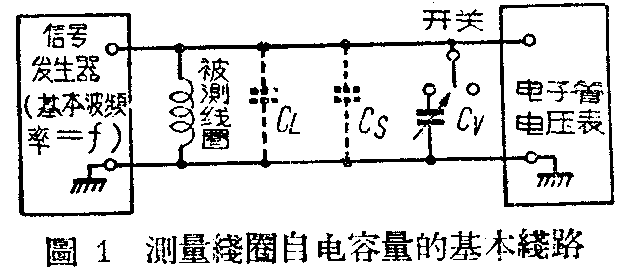
测量线圈自电容量的第一步是把CV自线路中去除。此时,与线圈调谐的电容量是并联的Cs和CL。信号发生器调节到谐振于其输出的二次谐波,这由电子管电压表的峰值读数表明(使用二次谐波的过程后面详述)。线圈谐振的真实频率并不重要,我们指定其为2f,而f是其基本频率。
当线圈和C\(_{S}\)、CL组成的槽路谐振于信号发生器输出的二次谐波时,下述的关系是肯定的:
2f=\(\frac{1}{2π}\)\(\sqrt{L}\)(C\(_{S}\)+CL) (1)
L是线圈的电感量。
不去动信号发生器的频率,而把可变电容器C\(_{V}\)接通到线圈的两端。然后调节CV直至线圈和C\(_{S}\)、CL 、C\(_{V}\)组成的槽路谐振于信号发生器的基本频率,可以由电子管电压表另一次峰值读数指出。现在谐振频率已是f,这时与线圈调谐的电容量是并联的CS、C\(_{L}\)和CV。此时
f=\(\frac{1}{2π}\)\(\sqrt{L}\)(C\(_{S}\)+CL+C\(_{V}\)) (2)
混合方程式(1)及(2)我们获得
\(\sqrt{L}\)(C\(_{S}\)+CL)
=\(\frac{2}{2π}\)\(\sqrt{L}\)(C\(_{S}\)+CL+C\(_{V}\)),
∴1\(\sqrt{L}\)(C\(_{S}\)+CL)
=2\(\sqrt{L}\)(C\(_{S}\)+CL+C\(_{V}\)),
∴\(\sqrt{L}\)(C\(_{S}\)+CL+C\(_{V}\)),
=2\(\sqrt{L}\)(C\(_{S}\)+CL),
∴L(C\(_{S}\)+CL+C\(_{V}\))=4L(CS+C\(_{L}\)),
∴ C\(_{S}\)+CL+C\(_{V}\)=4CS+4C\(_{L}\),
∴ C\(_{V}\)=3CS+3C\(_{L}\)=3(CS+C\(_{L}\)),
得 C\(_{S}\)+CL=\(\frac{1}{3}\)C\(_{V}\)(3)
如上所见,并联后的线圈自电容量和信号发生器以及电子管电压表的分布电容量之和,在调整到谐振时是等于C\(_{V}\)的三分之一。信号发生器的频率和线圈电感量不包括在这式中。
可以有趣地指出,上述方法还以近似高度精确地获得线圈的电感量;虽然此时除了电容量C\(_{V}\)外需要知道谐振频率f。
自方程式(2),我们得 \(\sqrt{f=}\)\(\frac{1}{2π}\)L(C\(_{S}\)+CL+C\(_{V}\)), ∴ f\(^{2}\)=1;4π2L(CS+C\(_{L}\)+CV), ∴ L=\(\frac{1}{4π}\)\(^{2}\)f2(C\(_{S}\)+CL+C\(_{V}\))根据方程式(3)CS+C\(_{L}\)=1;3CV, 得 L=\(\frac{1}{4}\)\(^{π}\)2f\(^{2}\)4;3C\(_{V}\)=\(\frac{3}{4ω}\)2CV, 其中ω=2πf。 2 f\(\sqrt{ }\)
路
2821
?