可变电容器通常应用在收音机和各种测试仪器中,收音机内有了可变电容器之后,才可以选择不同的电台,它的作用和自动电话里的拨号盘是一样的。可变电容器有各种不同的形状,但都少不了一组动片和一组定片。动片可在定片的间隙里面转动,转动以后,两组的相对面积有了变化,因此,电容量也随着改变,但改变的情形和动片的形状有关。我们为了使用上的方便,希望电容量按一定的规律变化,那么,它的动片的形状应当要有一定的关系。
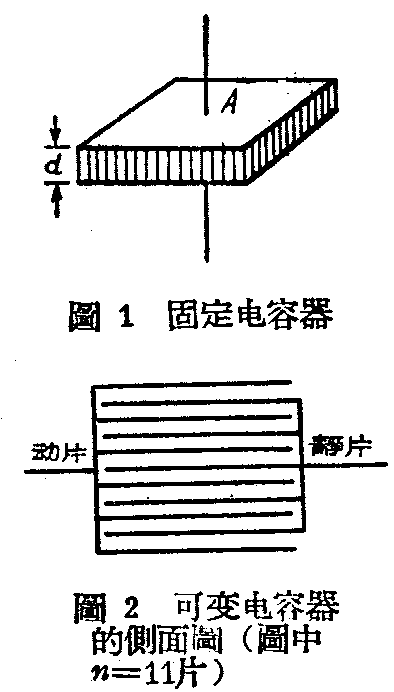
设有一个最简单的电容器(图1),用两块金属片做成,金属片的面积为A,两片间的距离为d,中间充填了介电常数为K的介质,它的电容量就是:
C=\(\frac{KA(公分}{^{2}}\))3.6πd(公分)微微法……(1)
假若两金属片的中间,不充填介质,那就充满了空气,这样的电容器,称为空气电容器。因为空气的介电常数为1(K=1),它的电容量就变为:
C=\(\frac{A(公分}{^{2}}\))3.6πd(公分)微微法……(2)
当动片和静片各有许多片时,并且把它们如图2那样的装在一起,假设总共片数为n,等于有了像图1那样的(n-1)中简单的空气电容器相并联,所以总电容量:
C=(λ-1)\(\frac{A(公分}{^{2}}\))3.6πd(公分)微微法……(3)
可变电容器通常有4种形式:直线电容式、直线频率式、直线波长式和指数式。由于这4种电容器动片的形状不同,转动后动片与定片的相对面积就不一样,因此电容量的变化规律也不同了。
直线电容式
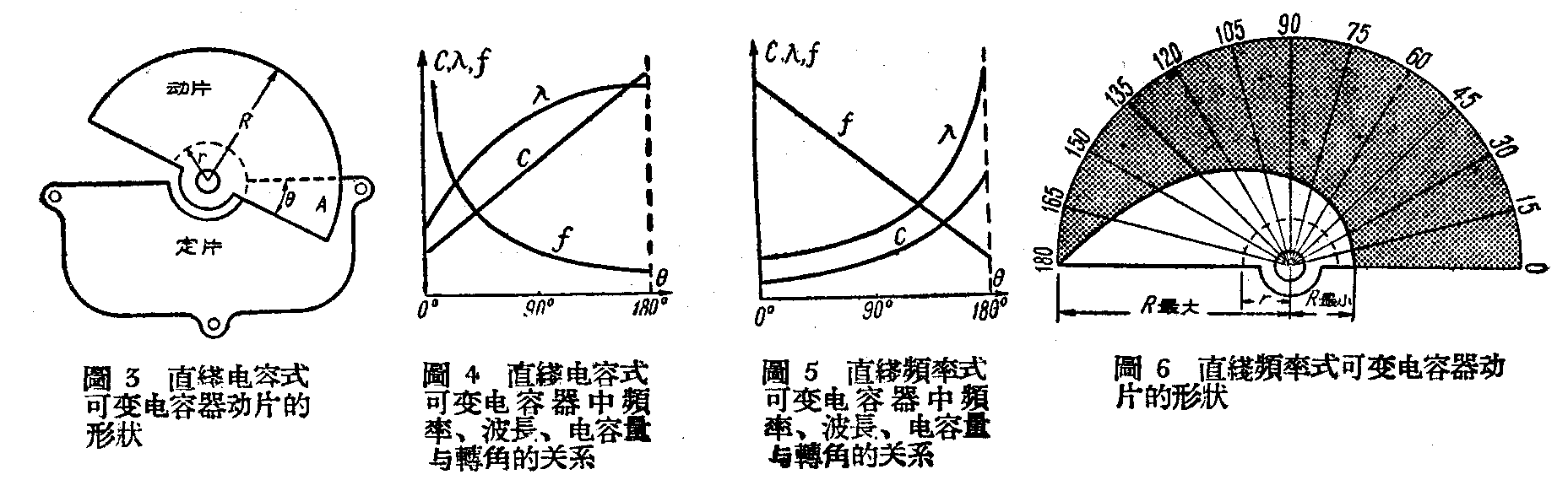
这种电容器的动片是半圆形的,构造比较简单,动片转入定片部分的面积A和转动角度θ成正比(图3)。假设动片的半径为R,定片的内圆半径为r,那么末面积A与转角θ就有
A=\(\frac{R}{^{2}}\)-r22θ ……(4)
把它代入到公式(3)中,得到
C=(n-1)\(\frac{R}{^{2}}\)-r27.2πdθ ……(5)
式中θ是以弧度计。当动片全部转入时,θ=π,电容量最大。在这个时候,最大电容量C\(_{m}\)=(n-1)\(\frac{R}{^{2}}\)-r27.2d微微法。
由于A和θ成正比,所以电容量C和转角θ成直线关系,而θ与频率f及波长λ就成为图4那样的曲线关系(因为f=\(\frac{1}{2π}\)LC\(\sqrt{,}\)λ=3×10\(^{8}\);f,波长与频率成反比)。正因为C与θ有直线关系,所以在刻度盘上可以按照角度均匀的刻上电容量的数值,也就是说,每转一个刻度时,所增加的电容量是一样的。在测试仪器中,如电容电桥,可变标准电容器时,就要用这样的电容器,而在无线电收音机里,希望频率有均匀的增减,因此,就不大适宜了。
例1:动片半径R=5公分,定片内圆半径r=1公分,每片间的距离d=0.2公分,共有19片,转到任意角度时的电容量:
Cθ=18\(\frac{25-1}{7.2×0.2π}\)θ=95.6θ微微法。
当θ=π时,最大电容量
C\(_{m}\)=18
直线频率式
这种电容器的转角和频率成直线关系,因此,动片的半径就不能等于一个常数,而必须随着转角而改变。
假设动片的最大半径为R\(_{m}\),定片的内圆半径为r,最大频率对最小频率的比值为β(β=f最大f最小),它的半径R和转角θ的关系为:
R=\(\frac{\sqrt{R}}{^{2}}\)\(_{m}\)-r2[β-(β-1)θ;π]\(^{3}\)+r2…………(6)
在任意转角时的电容量
Cθ=(n-1)(R\(^{2}\)\(_{m}\)-r2)14.4d(β-1)
{\(\frac{1}{[β-(β-1)}\)θ;π]\(^{2}\)-\(\frac{1}{β}\)2}微微法…………(7)
当θ=π时的最大电容量
C\(_{m}\)=(n-1)(R\(^{2}\)m-r2)14.4d-(β-1)[1-1;β\(^{2}\)]微微法…………(8)
用这种电容器时,刻度盘上可以按转角均匀的刻上频率数值。就是说转角和频率成直线关系;而对波长及电容量自然不是直线关系(图5)。有些音频振荡器、高频发生器和频率表中,就要用这种电容器。用了这样的电容器后,每转一个刻度时,所减小的频率是不变的。
例2:设R\(_{m}\)=5公分,r=1公分,β=3,总片数为23,要求Cm为80微微法,求出每片间的距离d应为若干公分?
用公式(6)求出R与θ的相对值:
θ(度) 0° 15° 30° 45° 60° 75° 90° 105° 120° 135° 150° 165° 180°
(公分) 1.37 1.43 1.50 1.59 1.69 1.83 2.00 2.22 2.47 2.81 3.32 4.01 5.00
根据这些数值,可以画出如图6的动片形状,并由公式(8)得到:
C\(_{m}\)=22\(\frac{5}{^{2}}\)-114.4d×2[1-1;9]=80,
所以d=0.227公分。
任意转角时的电容量
Cθ=80.7[1(3-2θ;π)\(^{2}\)-
直线波长式
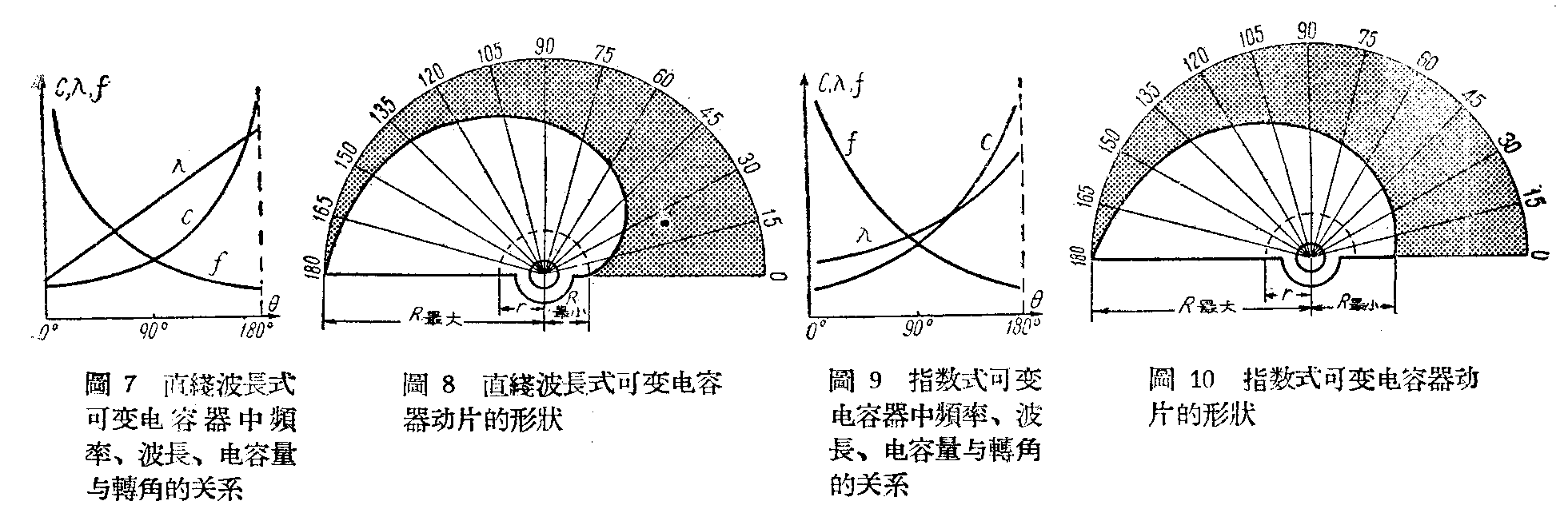
在直线波长式的电容器中,转角和波长成直线关系,而与频率和电容量就成如图7那样的曲线关系。因此,在刻度盘上对波长来说是均匀分布的。这种电容器也可用在收音机中,主要是用在波长表中。在波长表中用了这样的电容器后,每转一个刻度时所增加的波长数目是一样的。这样,当指针在两刻度之间时,就可以准确地估计出波长的数目了。
为了要保持转角与波长成直线关系,动片的半径也要随着转角而变化。设R\(_{m}\)和r与上面的意义相同,那么在任意角度时的动片半径R为:
R=\(\sqrt{(R}\)\(^{2}\)\(_{m}\)-r2)\(\frac{θ}{π}\)]+r\(^{2}\)…………(9)
而在任意角度时的电容量
Cθ=(n-1)\(\frac{(R}{^{2}}\)\(_{m}\)-r2)14.4π2dθ\(^{2}\)微微法 …………(10)
最大电容量
C\(_{m}\)=(n-1)\(\frac{(R}{^{2}}\)m-r2)14.4d微微法 …………(11)
例3:设R\(_{m}\)=5公分,r=1公分,d=0.25公分,最大电容量Cm=120微微法,求片数n?
先要根据公式(9)求出R与θ的数值:
θ(度) 0° 15° 30° 45° 60° 75° 90° 105° 120° 135° 150° 165° 180°
(公分) 1.00 1.73 2.24 2.64 3.00 3.31 3.61 3.87 4.12 4.36 4.58 4.79 5.00
由这些数值可以画出图8的动片形状,由公式(11)得到:
C\(_{m}\)=(n-1)\(\frac{5}{^{2}}\)-114.4×0.25=120微微法;
所以
n=\(\frac{120×14.4×0.25}{24}\)+1=19片;
在任意转角时的电容量
Cθ=
指数式
指数式电容器的特点是频率、波长和电容量在整个刻度盘上的变化率是一定的,但转角θ与频率f波长λ和电容量C都不成直线关系(图9)。它的动片半径
R=\(\frac{R}{_{m}}\)ee\(^{θ;π}\)…………(12)
式中e是自然对数的底,等于2.718。任意转角时的电容量
Cθ=(n-1)[(R\(_{m}\);e)\(^{2}\)(e\(\frac{2θ}{π}\)-1)-2r\(^{2}\);πθ];14.4d微微法………(13)
最大电容量则为:
C\(_{m}\)=(n-1)\(\frac{[0.87R}{^{2}}\)m-2r2]14.4d………(14)
例4:设n=23,r=1公分,d=0.3公分,C\(_{m}\)=100微微法,求动片的最大半径Rm?
由公式(14)得到
C\(_{m}\)=22\(\frac{[0.87R}{^{2}}\)m-2]/14.4×0.3=100
所以
R\(_{m}\)=\(\frac{\sqrt{1}00×14.4×0.3}{22}\)+2)1;0.87≈5公分;
把这个R\(_{m}\)代入到公式(12)中,求得R与θ的相对值:
θ(度) 0° 15° 30° 45° 60° 75° 90° 105° 120° 135° 150° 165° 180°
(公分) 1.84 1.99 2.17 2.38 2.56 2.78 3.03 3.31 3.58 3.86 4.22 4.59 5.00
由这些数值,就可画出图10的动片的形状。
任意转角时的电容量
Cθ=173(e\(\frac{^{2θ}}{π}\)-1)-32.6θ微微法。
现在的收音机中,大部分都采用了这种电容器,因为这种电容器每转一个刻度的时候,它的变化率是不变的,例如,在1000千周时,转动一个刻度时频率变化为10千周,即是变化率为1100,那么在1500千周的刻度上,转一个刻度时,频率的变化就是15千周了。在收音机中用了这种电容器后,就增大了可能接收的频率范围。(高煜)