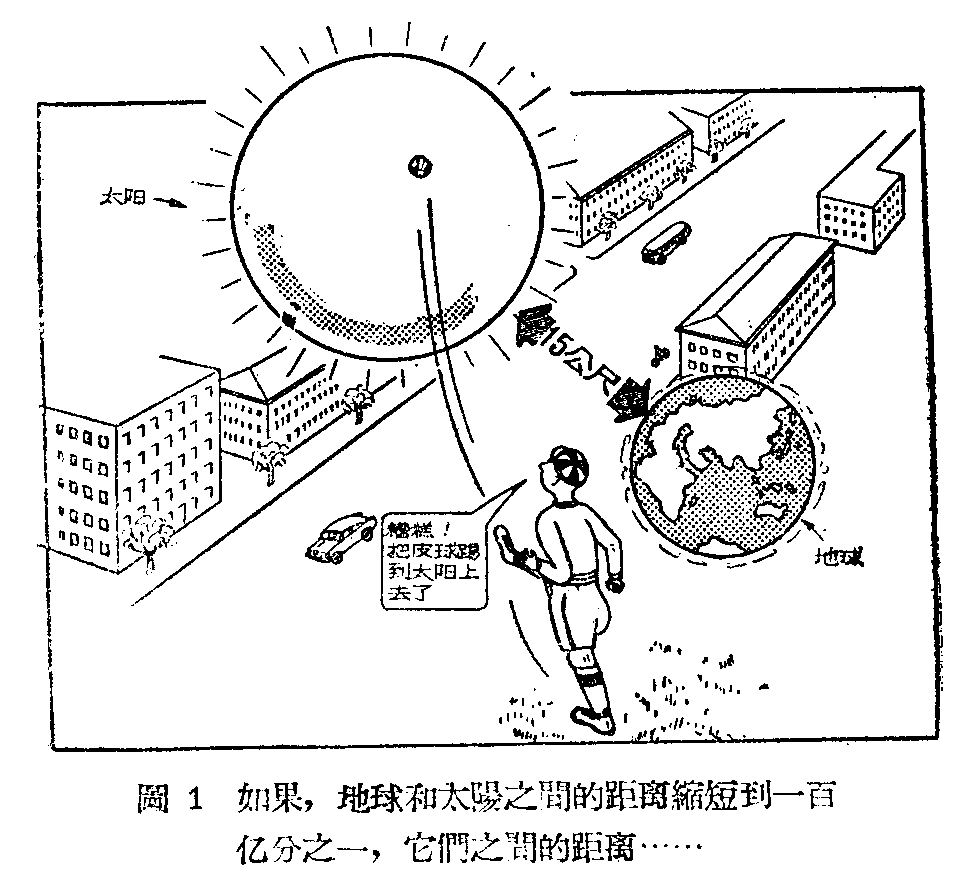
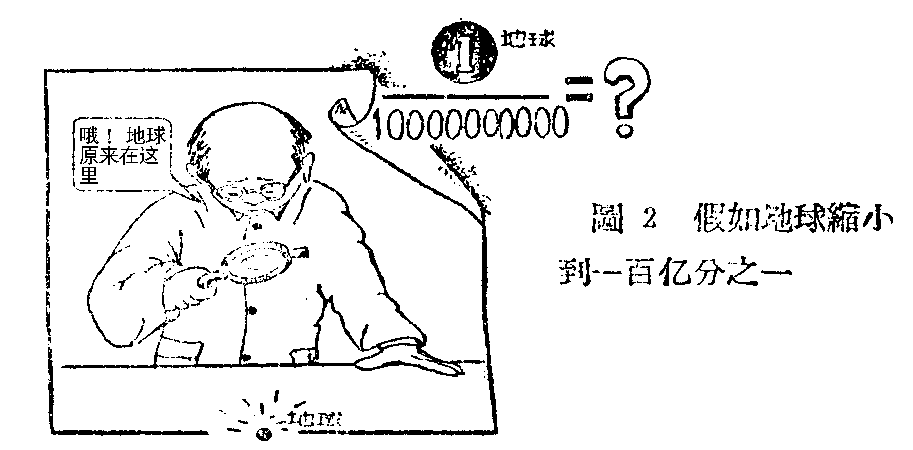
无线电电子管内所达到的真空程度,使得管内剩余的空气约为抽空前的一百亿分之一。减少到百亿分之一是巨大的减少。如果地球和太阳的距离缩短到百亿分之一,那么太阳离开地球就只有十五公尺,和一般街道的宽度差不多(图1)。如果地球缩小到这样的程度,那么它将变成为直径约一公厘的小颗粒(图2)。
即使在这样高度的真空下,普通大小的电子管(如6K3)里也还剩有40×10\(^{12}\)(40,000,000,000,000)个分子。
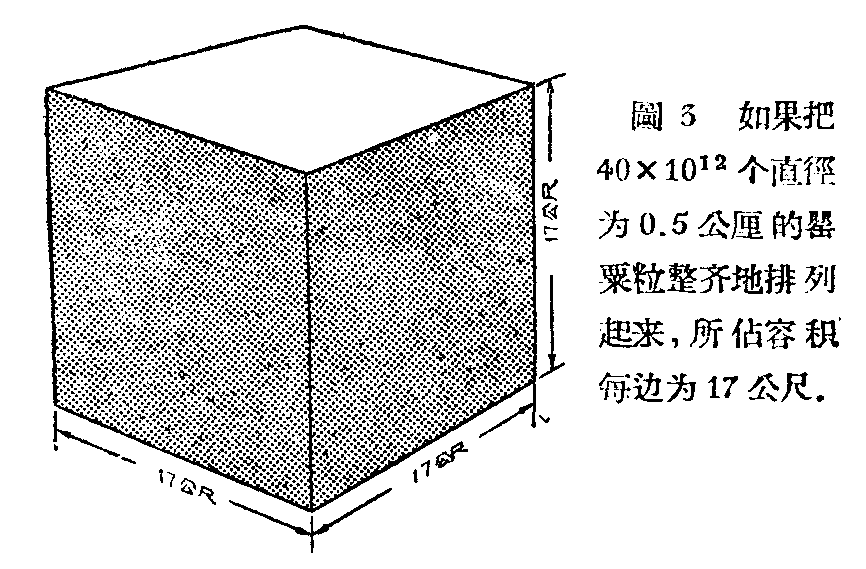
这个数字是巨大的。最微小的罂粟粒的直径约半个公厘。如果把这种颗粒整齐地排列起来,一立方公厘的体积可排列八个。把40×10\(^{12}\)个这样的颗粒堆放起来,要占多大的体积呢?
简单的计算表明,为了储存这么大数量的罂粟粒,需要容积为五千立方公尺的房间,即这么大容积的立方体,其各边约为17公尺(图3)。
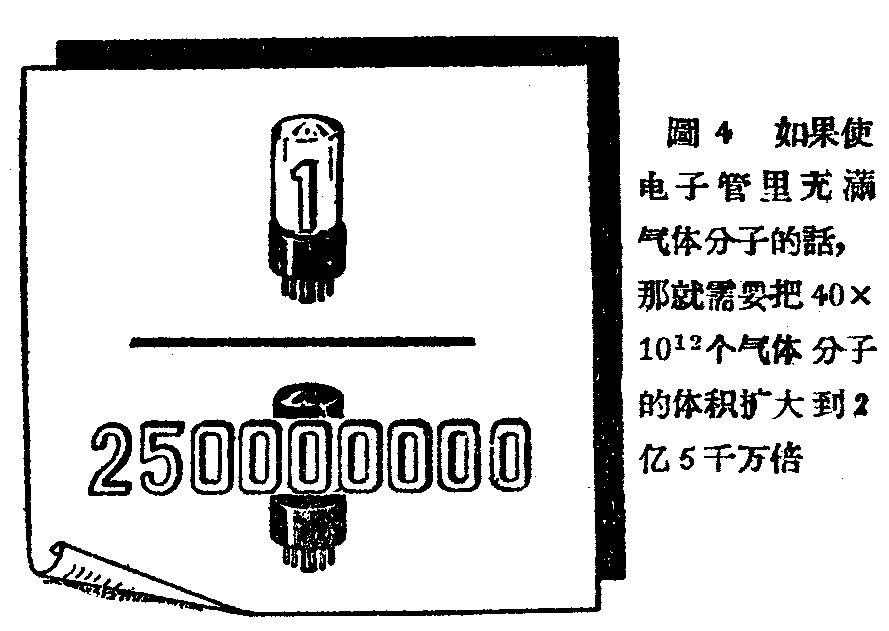
但是,分子是如此之小,甚至把几十万亿个摆开,也只占极小极小的体积。气体分子的直径一般为1×10\(^{-}\)3(0.000001)公厘,即百万分之一公厘。如果把电子管内剩余的40×1012个分子紧密地排在一起,那么它们的体积共占4×10\(^{-}\)5立方公厘,等于电子管体积的二亿五千万分之一(图4)。电子管内剩余的分子,在平均分布的情况下,每一立方公厘约包括80,000个分子。
这个数目也是很大的。但为了对分子与分子之间的距离有个正确的概念,必须把所有数值换成我们日常所习惯的大小比例。
如果使80,000个分子平均分布在一立方公厘的体积内,则各分子间的距离约为O.02公厘。这个距离相当于分子直径的20,000倍。我们可以与天文上的数值作比较。地球和月亮之间的距离大约等于地球直径的25倍。如果不去比较它们的绝对值,则可认为地球和月亮间的距离似乎比电子管内分子与分子之间的距离近1000倍(图5)。为了更好地理解这个问题,我们再谈到罂粟粒。如果使两个最小的罂粟粒离开的距离等于它们直径的20,000倍,则两个颗粒相距10公尺。把这个概念折成我们日常生活的住宅面积,则好像是在一间面积50平方公尺的房间内,有两颗罂粟粒。

如此看来,一个大房间里摆着两颗罂粟粒,这便是电子管抽气后气体分子分布的密度。显然,电子在从阴极飞向屏极时,在通路上几乎不会碰到空气的分子;相碰的现象只在极少有的特殊情况下,才会发生。(翁光宗 译)