调谐回路是怎样起作用的

在无线电里，电子管是很巧妙的东西，但电子管不和其他零件配合起来，就不能发挥它的作用。现在，我们就来谈谈电子管的一个得力助手——调谐回路，看它们在我们已经谈过的放大器和振荡器里是怎样起作用的。

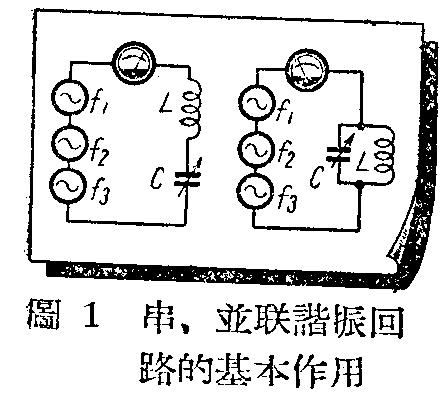
调谐回路有串联和并联两种，都是用线圈和电容器组成的，它们的基本特性我们已经晓得，就是在谐振时，串联回路两端的电阻最小，通过的电流最大；并联回路两端的电阻最大，通过的电流最小（图1）也往往在无线电线路图里，乍一看串、并联回路很容易混淆。例如图2是某个收音机的部分线路图，上面绘着6个谐振回路。L\(_{1}\)C1组成的“陷波器”是并联回路，转动C\(_{1}\)到这回路对一干扰电台的频率谐振时，a、b两端的电阻最大，因此天线里的干扰电流最小，就像干扰电波在这里是落入陷井里了一样，大大地减小了它的干扰作用。而L2C\(_{2}\)则组成一串联谐振回路，转动C2可以对所接收的信号频率谐振，因此天线里这频率的电流最大，同时L\(_{1}\)C1对这频率并不谐振，电阻不大，所以地由a到b的信号电流影响不大。这两个回路一个是并联，一个是串联的，看样子就很容易认识。图中虚线所绘的e\(_{1}\)，e2，e\(_{3}\)等，代表外来电波在天线里感应出的电动势，这些电动势在天线里产生频率为f1 ，f\(_{2}\)，f3等的电流，经过并联回路时，都有两条路可走，而经过串联回路时，只有一条路可走。

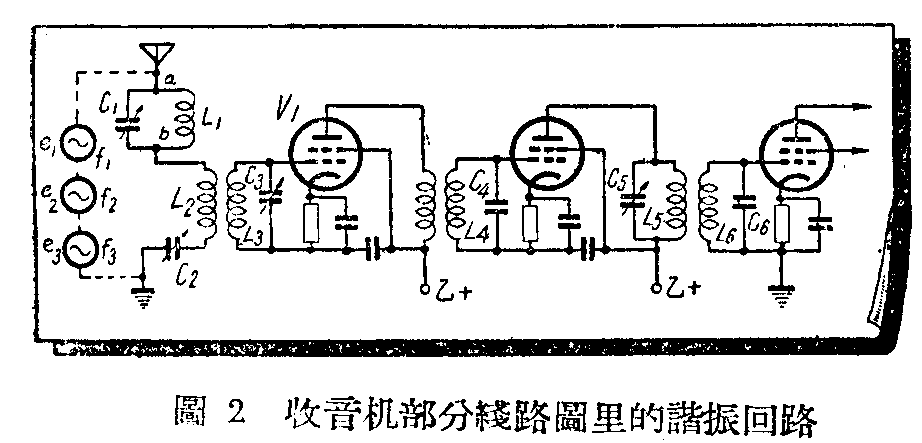
但图中L\(_{3}\)C3，L\(_{4}\)C4，L\(_{6}\)C6乍看都像是L和C并联的，其实它们都是串朕谐振回路。拿L\(_{3}\)C3来 说，当L\(_{2}\)里有电流时，在L3里便感应出一电动势e\(_{0}\)，这电动势所产生的电流要经过L3和C\(_{3}\)，只有一条路可走，所以L3C\(_{3}\)是串联谐振回路。谐振时，很小的感应电压，使产生很大的电流，这电流经过C3，便在C\(_{3}\)两端产生很大的电压降ec，加到电子管V\(_{1}\)的栅极上去，使V1管有比较大的屏流输出。e\(_{c}\)比e0大的倍数，便是这串联回路的电压增益。同样道理，L\(_{4}\)C4和L\(_{6}\)C6都是串联谐振回路，都和 L\(_{3}\)C3起同样的作用。图中的L\(_{5}\)C5则是并联谐振回路，因为从电子管屏极输出的高频电流，可以同时走L\(_{5}\)和C5两条支路，回到阴极去。

图3甲和乙是两种电子管振荡回路。显然，图甲里L\(_{1}\)C1和L\(_{2}\)C2，都是串联的，和图2里的L\(_{2}\)C2及L\(_{3}\)C3相似。可是图3乙的L\(_{1}\)C1和L\(_{2}\)C2都是并联回路。由于L\(_{1}\)C1谐振时电阻高，所以很小的屏流在L\(_{1}\)C1上便可以产生很大的电压降，这电压降e在电子管屏极和栅极间电容量C\(_{gp}\)、Cc和L\(_{2}\)C2所组成的回路里，产生电流i(图4），在L\(_{2}\)C2。这里有两条路可走，所以L\(_{2}\)C2是并联谐振回路。这里，很小的电流i又在L\(_{2}\)C2。两端产生很大的电压，加到栅极上，影响屏流，再在L\(_{1}\)C1上产生电压。这样的作用来回重复，便产生振荡。

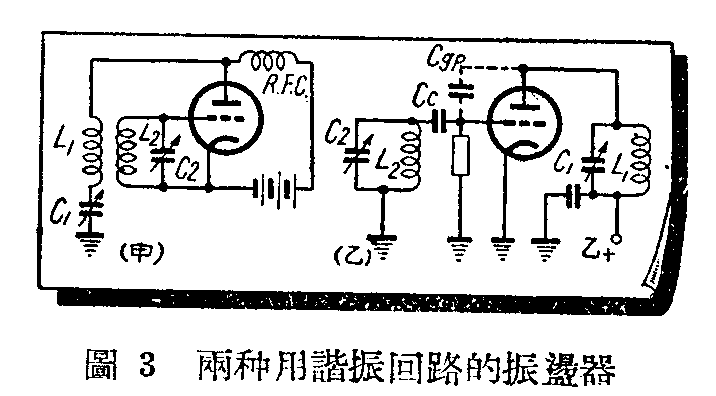
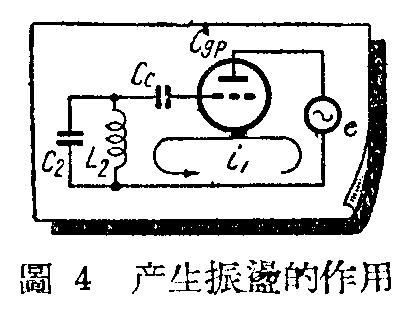
所以要看一个谐振回路是串联还是并联，不能只看线圈和电容器在线路图上的连接法，要看通过这回路里的电流是怎样的走法。

会辨别串、并联谐振回路，还只是最基本的知识。如果我们注意看一部收音机里的零件，会发现往往两个谐振回路（如图2的L\(_{4}\)C4和L\(_{5}\)C5），调谐的频率相同，但所用线圈和电容器并不是一样大小。各种谐振回路里L／C比值的大小，是无线电里极重要的一个技术问题，懂得这个问题后，才可以更进一步地了解谐振回路的妙处。

一个谐振回路的构成者，L和C，对所调谐的频率f\(_{0}\)能够谐振，要符合f0=\(\frac{1}{2π}\)\(\sqrt{LC}\)的关系，这是一项基本任务。要得到这一关系，L和 C的乘积有一定的数值。L大C就要小；L小C就要大。到底L/C的比值应当是大还是小，要看谐振回路是串联还是并联，并且要看它的具体任务而定。就像一队球员个个都要打球，这是基本任务，但他们还有前锋、中锋、后卫之分，由于具体任务不同，所以技能不完全一样。同样，担任不同任务的谐振回路，也应当有不同的性能。

一般谐振回路的具体任务不外是：（1）选择一个频率，产生这个频率的大电流、电压或电阻，（2）消除一个频率的影响，使它不发生干扰或不良的作用，（3）储藏一个频率的电能，产生振荡，（4）抑制一个频率的谐波。（5） 通过一个频带等。

例如图2的L\(_{1}\)C1的具体任务是消除一个干扰频率而让其他频率顺利通过；L\(_{2}\)C2是要选择一个所要接收的频率f\(_{s}\)；L3C\(_{3}\)、L4C\(_{4}\)和L6C\(_{6}\)是要产生频率fs的最大电流和电压增益；L\(_{5}\)C5的具体任务是产生一个大电阻，使V\(_{2}\)电子管有相当大的负荷电阻，得到足够大的电压放大作用。又例如图3甲和乙里的L2C\(_{2}\)，都是振荡回路，我们希望给他很小的电能，就能够维持里面有一个高频率的电流振荡。而在图3乙里的L1C\(_{1}\)上，最主要的是得到尽可能大的电压来维持L2C\(_{2}\)的振荡，所以L1C\(_{1}\)必须要有很大的谐振电阻。

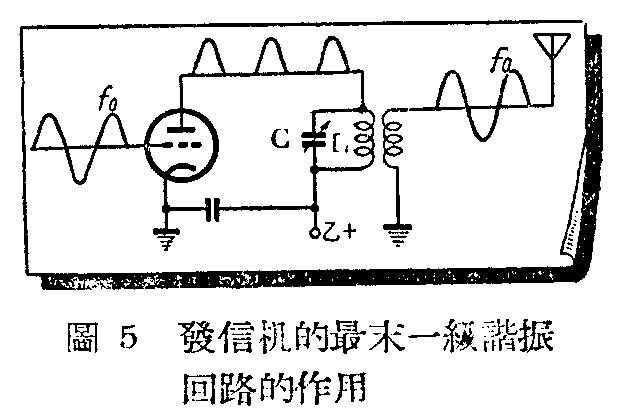
图5里的L、C，是发信机最末一级的屏极输出调谐回路，栅板上所加的频率是f\(_{0}\)，我们希望天线上的电流频率也是f0，但这屏流的波形很特别，完全不像一个正弦波，分析起来它除了含有频率为f\(_{0}\)的分量外，还有2f0， 3f\(_{0}\)……等谐波分量，因此 LC的主要任务就是要抑制这些谐波。

至于图2里的 C5L5和L6C6两个回路，都对一个频率谐振，它们相互发生感应交连时，会发生一种特殊的作用，就是能够通过一个频带。我们说过，声音是被载波带来的，载波加声音后，就不只一个频率，而是占一个频带，现在就是让这个频带打这里顺利的通过，而在这频带以上和下面的频率便不能顺利通过。所通频带的宽窄，决定于两回路间感应交连松紧的程度，而和每个谐振回路的L／C值没有直接连系。

上面所举的这些谐振回路（通过一个频带的情形除外），都有着不同的具体任务，它们能够完成自己的特殊任务，主要是因为它们有不同的L/C比值。下面我们就来谈这是什么道理。

关于L／C比值的分析，我们最好是从“选择性”谈起。串、并联回路都有选择性好坏的分别。选择性好的回路，在谐振频率f\(_{0}\)所表现的性能，和它们在和f0相隔极近的频率所表现的性能差别很大。例如一个选择性好的并联谐振回路，在f\(_{0}\)时它变成一个高值电阻，但频率在f0上下极近时，它的阻抗值就很低；一个选择性好的串联谐振回路，谐振时变为一个低值电阻，而微微失调时，就有很高的阻抗。因为有这种性能，所以才能从许多频率中把自己所谐振的频率，突出地选择出来。

要一个并联谐振回路有良好的选择性，除了当它谐振时电阻必须相当大以外，重点还在于稍微去谐时，阻抗的减小就特别大；一个串联谐振回路有良好选择性，除了当它谐振时电阻必须相当小以外，重点还在于稍微去谐时，电阻的增加就特别大。要得到这种特性，拿并联回路来说，它的C要大而L要小。因为C大时，C的容抗X\(_{C}\)就小； L小时，L的感抗XL就小。所以通过C和L的电流i\(_{C}\)和iL平时都很大，而且在不谐振时，X\(_{C}\)不等於于XL，i\(_{C}\)也不等于iL。从前我们分析并联谐振回路时，曾经指出i\(_{C}\)和iL的相位相差180°，实际是它们相减才得出流到这回路里去的总电流i\(_{t}\)。现在iL不等於i\(_{C}\)，而且iL和i\(_{C}\)都很大，所以它们的差it总是相当大，换句话说，微微不调谐时，这谐振回路对总电流的阻抗便很小。唯有在谐振时，X\(_{L}\)=XC，i\(_{L}\)=iC,i\(_{L}\)和iC有完全对消的作用，所以i\(_{t}\)才非常小。所以说并联谐振回路选择性好的条件就是C大L小，即L／C 比值小。这样的回路，如果调谐频率是f0，显然一定会有消除邻近频率干扰的特性（如陷波器），也有抑制2f\(_{0}\)，3f0等频率的特性（如发信机输出的电槽）。

一个串联谐振回路，我们曾经指出它在各方面都和并联谐振回路相反，这里的条件也恰好相反，即选择性良好的串联谐振回路，一定足L大C小，即L/C比值大（如图2里的L\(_{2}\)C2）。

关于L/C比值大小的意义，我们可以举一个实例来说明。

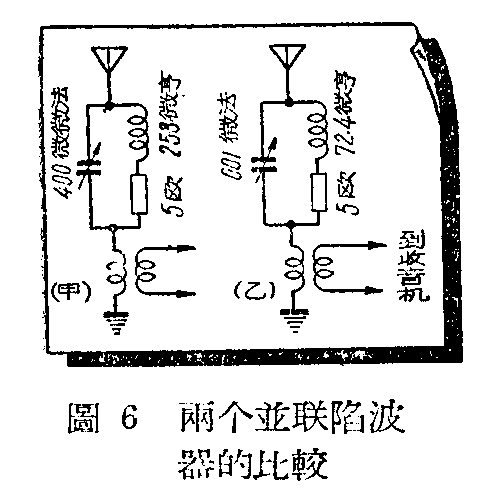
例如图6甲和乙的两个陷波器，（\(\frac{L}{C}\)）甲=253;0.0004=63250，（\(\frac{L}{C}\))乙=72.4;0.0014=51690,因为63250大于51690，所以图乙的陷波器选择性比较好。

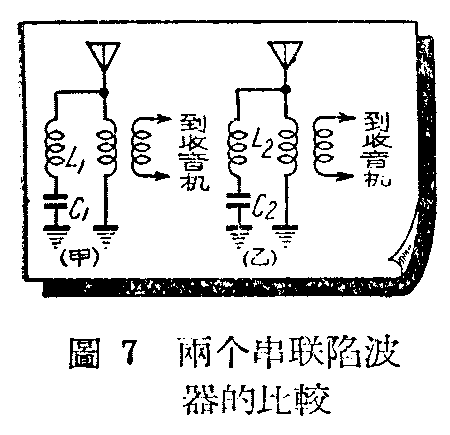
又例如图7甲里， L\(_{1}\)=28微亨，C1=100微微法；图7乙里，L\(_{2}\)=5.6微亨，C2=500微微法。L\(_{1}\)C1= L\(_{2}\)C2=2800，所以它们调谐的干扰频率相同，都能使它经低调谐电阻入地，不影响收音机。但（\(\frac{L}{C}\)）甲=28;0.0001=280000，（

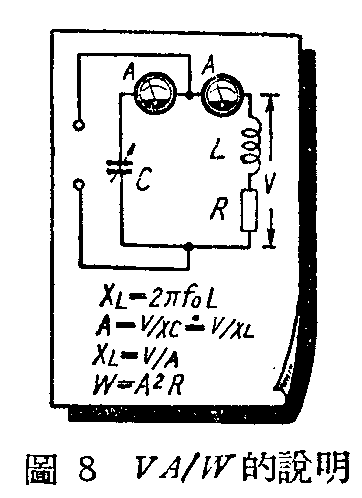
为了说明一个谐振回路的性能，除了用L/C比值外，在许多地方时常用它的Q来表示。对于谐振回路抑制谐波的性能，无线电工程师们也常用\(\frac{VA}{W}\)来表示。说法一多，就容易发生混淆。Q我们晓得是品质因数，它的数值基本上决定于谐振回路里的电阻R的大小，R愈大，消耗能量愈容易，即储能的本领愈差，Q=2πf\(_{0}\)L;R的值便愈小。\(\frac{VA}{W}\)比值中，V代表并联谐振回路两端的电压，A代表回路里的电流，而W代表消耗在回路里的电力，即等于A\(^{2}\)R（图8）。因此，

所以并联谐振回路的Q和\(\frac{VA}{W}\)原来是一件事的两样说法。一个振荡回路应当有很好的储能特性，所以它们的Q和VA;W值都应当很大。

我们要一个并联谐振回路（如图3乙）的\(\frac{VA}{W}\)和Q值大，首先是W=A\(^{2}\)R里的R要小，其次是A要大。要在R极小的情形下，A虽大并不显著地增加W，而同时显著地增加VA，所以VA;W大和Q大的条件，要求X\(_{C}\)和XL都小，因为这样A才会大。所以并联谐振回路储能良好的条件也是C大L小，和它的选择性好的条件相同，即都是\(\frac{C}{L}\)比值大。这就是一般收发信机的振荡回路里，电容器都比较大的缘故。

串联谐振回路的Q，虽仍是等于2πf\(_{0}\)L)R, 但这里没有相当于上面的VA的问题，主要是保持最大的谐振电流，得到最大的增益，减小R是最主要的办法。能够增大L而保持L;C比值大，同时并不增大R（R往往是线圈里的电阻），是既提高选择性又提高Q的最好方法。有许多好收音机里，用特制的铁粉心线圈来达到L大而R小的目的，就是这个缘故。图2的L3C\(_{3}\)、L4C\(_{4}\)和 L6C\(_{6}\)及图3甲里的L2C\(_{2}\)，都是根据这个道理设计的。

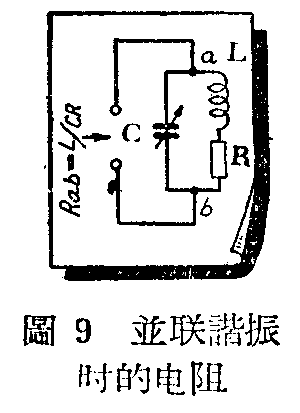
其次，我们再来谈谈怎样可以利用并联谐振回路产生最大电阻并且可以调整并联谐振回路的电阻的问题。用简单的数学可以证明当谐振时，并联谐振回路两端的电阻是：

因此，要得到最大的谐振电阻，可以增加\(\frac{L}{C}\)比值，同时尽量减少R（图9）。图3乙里的L\(_{1}\)C1就是这样设计的。用任何方法增减R，就可以相应地改变R\(_{ab}\)。在发信机的电力放大器里，电子管要求有一定的负荷电阻，才能输出最大的电力，同时输出又要尽量免除谐波，因此充屏极负荷的谐振回路的L/C比值应当小，必须在L/C小的情形下增减R来得到所需的负荷电阻。

上面，我们结合了许多实用电路，来讨论了一些怎样使用谐振回路的道理，了解了各种谐振回路在不同地方的特殊作用。但是谈这些问题时，还没有考虑到L或C值在一定范围内变化的情形。当L和C有变化时，会发生什么现象是更有趣的问题，我们留在谈收音机线路原理时再详细分析。（沈肇熙）