电子管特性曲线-Ⅱ

上次，我们谈了一些怎样绘电子管特性曲线的方法，和电子管静态特性曲线的几种简单用途。

电子管的静态特性曲线只和电子管本身的构造有关，它们是在电子管制成出厂时绘制的，在许多电子管手册中，都可以根据管名查到它的静态特性曲线。这些曲线，表示当各电极电压不变动（即静止），而仅改变一个电极的电压时，所有电流变化的情形。它们并不能说明当几个电极的电压同时改变时，电流是怎样变化的。在实际应用中，当一个电极上的电压有变动时，首先引起电流的变动，由于这电流的变动，又产生其他电极电压的变动。换句话说，从这种曲线，还看不出整个电子管在线路中的动态，所以被叫做静态曲线。

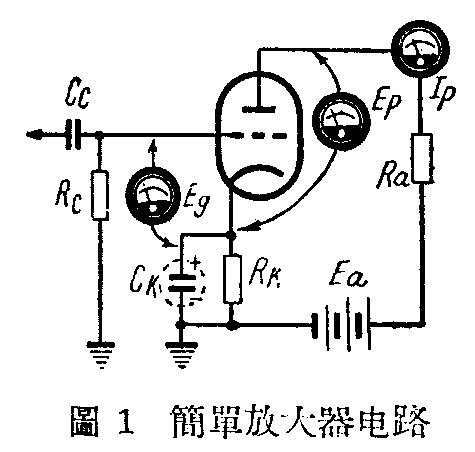
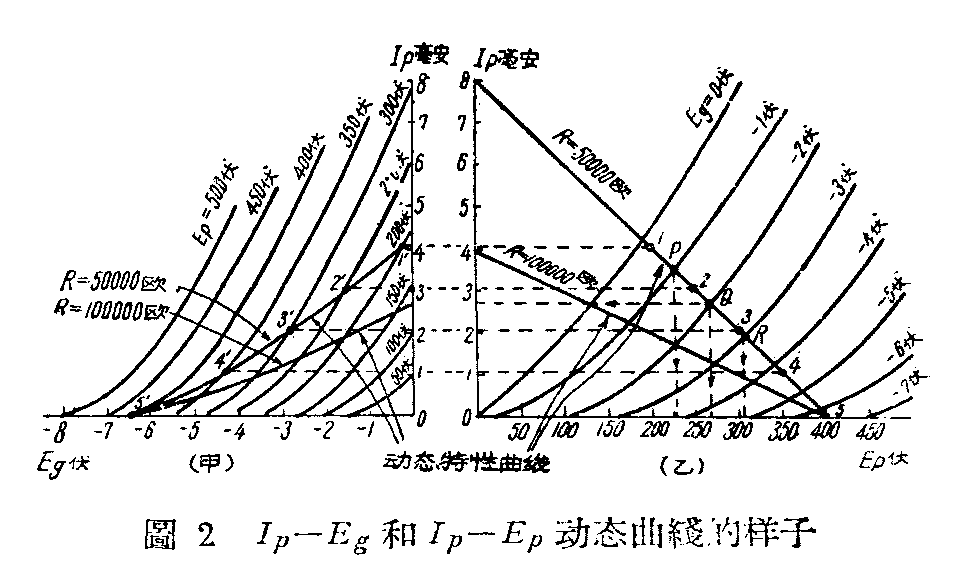
在实用电子管电路中（例如图1所示的放大器电路），当栅极加上交流电压时，先产生屏流I\(_{p}\)，流经电子管的负荷电阻Ra（为了要使电子管输出较大交流电压或电力，我们必须加负荷），便产生电压降I\(_{p}\)Ra，即当有I\(_{p}\)流动时，屏极电压就比电源电压小了IpR\(_{a}\)，如果Ip的大小受栅极的控制，随着栅极电压的变化而变化，那么屏极电压就会相应地发生变化。显然屏压并不是“静止”不动的了。尽管在有负荷的实际工作情形下，屏压E\(_{p}\)和栅压Eg同时变动，但我们还照旧可以测量出来在不同栅压时的屏压数值和屏流数值，在绘图纸上把它们之间的关系一点点的绘出来，这些曲线，就是电子管的动态曲线。电子管的动态曲线是随着负荷改变的，而电子管的负荷又是随着使用的情况改变的，例如电力放大管和电压放大管的负荷电阻，数值就大不相同。因此，电子管动态特性曲线只能根据千变万化的实际使用情况来分别决定，而不是工厂所能预先给出的。电子管手册里一般没有动态特性曲线，就是因为这个道理。为了方便起见，我们可以把动态曲线就绘在静态曲线一张纸上。图2甲和乙就是把一个苏联电子管6H9C的动态和静态特性曲线，分别绘在栅压一屏流及屏压一屏流两种静态曲线图上的情形。在各动态曲线上，我们还标明了所用负荷电阻的数值，显然的表示出动态曲线和负荷的关系。

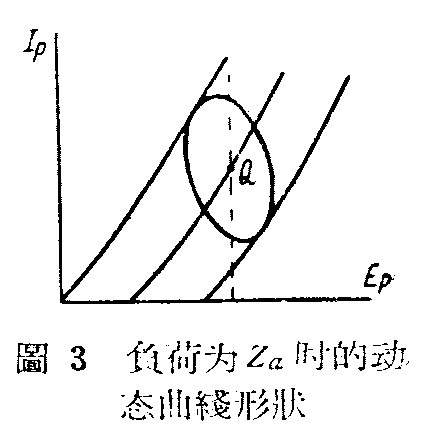
自然，电子管的负荷，不一定永远是纯电阻性质的，例如当一电子管的屏极电路里，接有一个线圈时，它的负荷就是含有电感性质的。如果我们实际一点点的测试，就会发现有阻抗负荷Z\(_{a}\)时的电子管Ip—E\(_{p}\)动态特性曲线，变成为圆形或椭圆形状如图3所示。

为了简单起见，我们只谈谈纯电阻负荷时动态特性曲线的绘法。

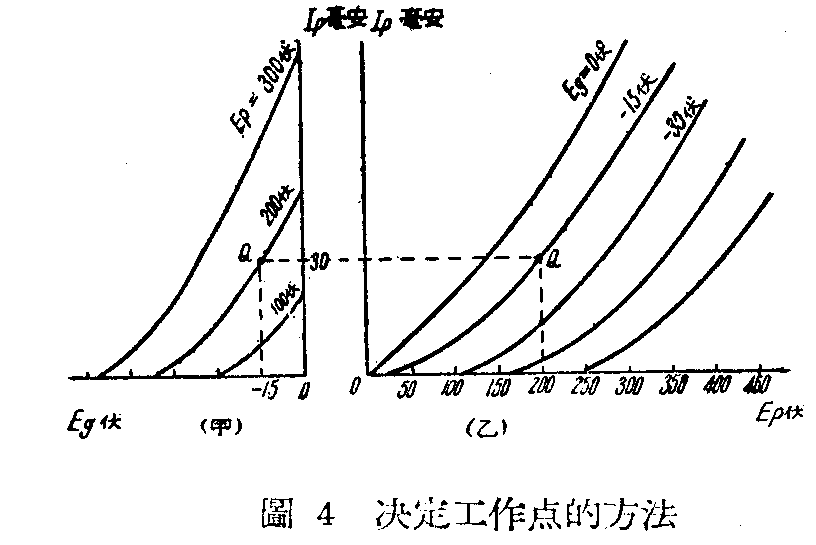
无论是在栅压——屏流或屏压——屏流静态曲线族上，加绘动态曲线，首先要找到所谓“工作点”Q。工作点就是当接有负荷后，任何电极的电压都还没有发生变化时，由电子管各极的电压和电流值所决的一个点。例如我们任意绘出两族I\(_{p}\)—Eg及E\(_{p}\)—Eg静态曲线如图4甲和乙，设加在电子管栅极上的电压是-15伏，屏压是+200伏，屏流是30毫安，那么我们便很容易在这两张图上定出点Q来。显然，动态曲线一定会通过Q点，在各极电压不断变动的过程中，只要有一个电极的电压某一瞬间的数值，恰好又变到等于没有变动以前的直流电压数值，那么它这一瞬间的工作点一定就是Q点。

在I\(_{p}\)—Eg静态曲线族上绘动态曲线，除了用实测的方法外，还可用数学理论求出动态关系的近似公式，然后根据公式，一点点的计算，最后连接许多点把曲线绘出来。这种计算如果只求近似值实际并不困难，但为了免除对所用的一些普通三角和级数问题作过多的补充讨论，我们这里不详谈这种计算方法。最简单的方法，是先绘动态I\(_{p}\)—Ep曲线，然后再根据它来求动态I\(_{p}\)—Eg动态曲线。

在I\(_{p}\)—Ep座标纸上绘动态I\(_{p}\)—Ep曲线，除了可用实测方法外，用计算方法同样准确，又十分方便，通常我们分析电子管在电路中的作用，多用动态I\(_{p}\)—Ep曲线，这又叫做“负荷线”。因为它比较简单实用，下面我们详细加以说明。

首先，我们解释一下“交流实效负荷电阻”的概念。以后为了区别起见，我们用R\(_{ac}\)代表交流负荷电阻，而用Rdc代表直流负荷电阻。

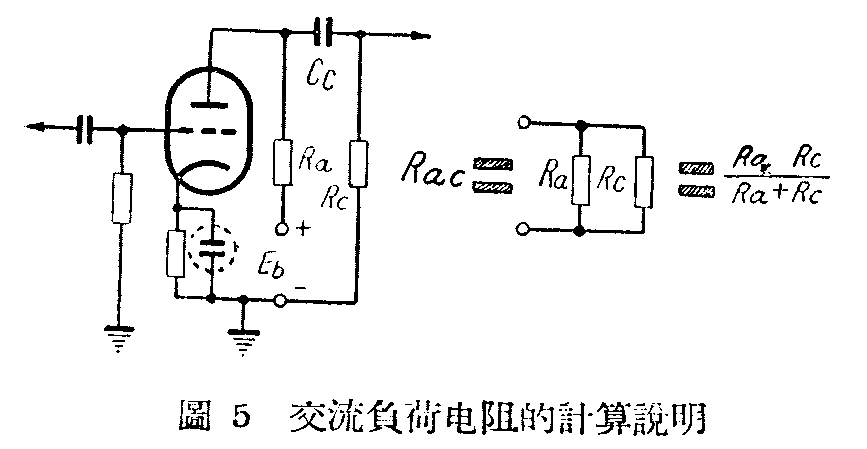
图5是一个电子管放大器的实际线路图。构成6H9C管的屏极输出回路的，有R\(_{a}\)，Cc和R\(_{c}\)等元件。很显然的，电子管的直流屏流部分只通过Ra，不会通过C\(_{c}\)而跑到Rc里去，所以R\(_{a}\)就是直流负荷电阻Rdc。我们说过，随着交流栅压变动的屏流，可以分成为一个直流屏流和一个交流屏流相加。因此，除了上述的直流屏流还有一个C\(_{c}\)不能阻挡的交流屏流。换句话说，交流屏流不仅通过Ra，它还通过R\(_{c}\)。通过Ra后的交流屏流是经电源E\(_{b}\)和机壳的连接回到阴极、通过Rc的交流屏流，也是经机壳的连接回到阴极（图中表接机壳）。所以对交流屏流来说。R\(_{a}\)和Rc实际是并联起来的两条通路，它们的并联电阻：\(\frac{R}{_{a}}\)RcR\(_{a}\)+Rc就是所谓“交流实效负荷电阻”R\(_{ac}\)。即Rac=R\(_{a}\)Rc;R\(_{a}\)+Rc。交流屏流在R\(_{ac}\)两端的变动，引起屏压作相应的变动，所以我们绘动态曲线，必须把Rac当为真正的负荷来看待。

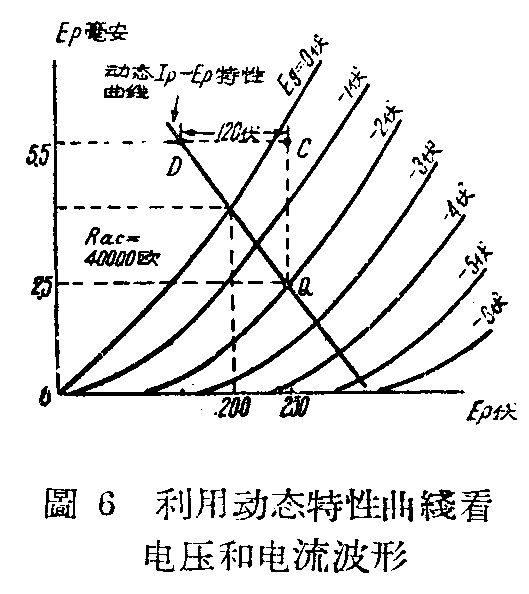
在I\(_{p}\)，Ep坐标纸上所绘的动态曲线，是一条直线，换句话说，由各个变动着的栅压，屏压和屏流所决定的各点，恰好都在一条直线上。这条直线的绘法很简单（参考图6）。假定不加交流栅压时的屏压是250伏，屏流是2.5毫安，栅压是-2伏，我们很容易定出Q点如图4乙。现在假设由于栅压的变动，使屏流增加了3微安，而使屏压减低了3×R\(_{ac}\)毫伏，假定Rac＝40000欧， 则3×R\(_{ac}\)＝3×40000＝120000毫伏=120伏。因此我们在Q点可绘一垂线，顺这垂线向上量一距离等于3毫安的变化，得点C，再经C点绘一水平线，并顺这水平线往左量一距离等于120伏的降压，得点D。然后通过D点和Q点绘一直线，这就是我们所要求的Ip—E\(_{p}\)动态曲线，也就是交流负荷线。

利用I\(_{p}\)—Ep动态曲线，我们很容易绘出I\(_{p}\)—Eg动态曲线（同时看图4甲和乙）。即把I\(_{p}\)—Ep动态曲线上各点的屏流和栅压值移到I\(_{p}\)，Eg坐标纸上，然后把这些点联起来，就是同一电子管的I\(_{p}\)—Eg动态特性曲线。例如图2甲中的1\(^{′}\)，2′，3\(^{′}\)，4′，5\(^{′}\)各点就是这样从图4乙中的1，2，3，4，5各点决定的。

利用动态I\(_{p}\)—Ep曲线，很容易求出放大器的放大倍数。例如在图5的电路中，如R\(_{a}\)=Rac=50000欧，共动态曲线和工作点Q如图2乙所示。当栅压E\(_{g}\)在-2-1=-3伏至-2＋1=-1伏之间变动时，电子管是在动态曲线上P、R间运用，由P、R点读出屏压Ep的相应变动为227伏至304伏。因此放大倍数为304-227-1-（-3）=77;2＝38.5倍。同时可以求出输出交流电压的峰值是\(\frac{304-227}{2}\)=38.5伏，有效电压输出为38.5;\(\sqrt{2}\)=38.51.414=27.2伏。

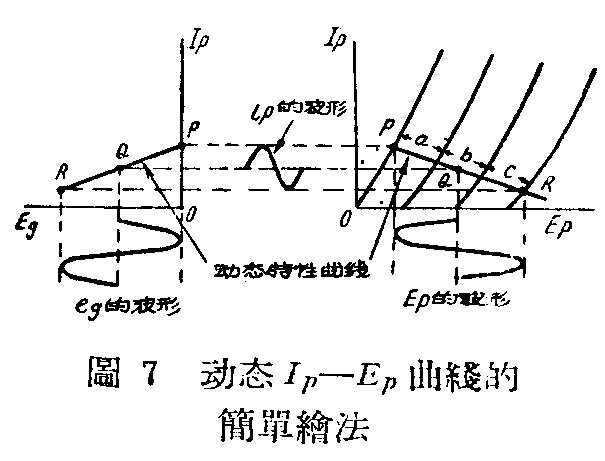
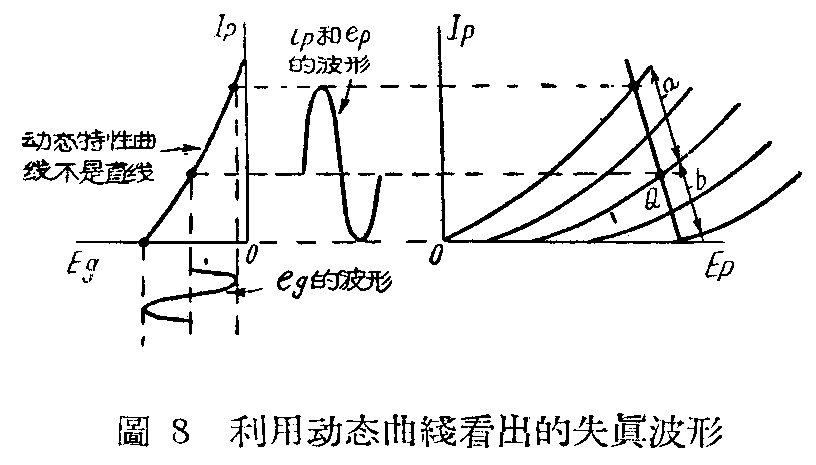
利用I\(_{p}\)—Eg和I\(_{p}\)—Ep动态曲线，可以看出放大器失真的大小和电波的波形。用公式计算失真度一般是相当繁琐的，而用动态曲线可以了解失真的实际情况，这就是动态曲线的优越性。图7表示当I\(_{p}\)—Eg动态特性曲线是直线时，在栅极上加一正弦电压，所得交流输出电流和电压（交流电压等于交流电流乘R\(_{ac}\)，故交流电压和电流波形相同）也都是正弦波形，因此没有失真，这时所使用的Ip—E\(_{p}\)动态曲线段和各静态曲线的交点是均匀间隔的（a＝b＝c＝……）。相反的，倘若Ip—E\(_{g}\)动态曲线不是直线，则所得交流屏流和输出电压都有失真，同时Ip—E\(_{p}\)动态曲线和静态曲线交点的间隔也不均匀（图8中，a≠b）。要免除失真，就需要改变栅压变动的范围，工作点的位置和交流负荷的大小，则恢复不失真的情况为止，这就使得我们能够在纸上先进行设计，决定屏压，栅压，负荷电阻和栅极激励电压的大小，把电子管使用得恰到好处。

利用动态曲线，我们既可以得出屏电变动的范围，求出交流屏压的有效值，同样我们也可看图得出交流屏流变化的范围，求出交流屏流的有效值，然后把交流电压和电流的有效值相乘，得出输出交流电功率。

这些计算，只需用简单的加、减、乘、除，就能解决实际问题，动态曲线的巧妙就表现在这些地方。当我们使用五极管或四极管，用同样简单的计算法看动态曲线，就可以决定帘栅极应当串联多大降压电阻，再接到电源；并可以决定阴极应当串接多大电阻来产生所需栅偏压。这里我们不详细举例说明。

我们灵活的使用动态和静态特性曲线，可以解决许多实际问题。例如当我们需要不失真的检波和放大时，就尽量挑选静态特性曲线较直较均匀的电子管，并使所使用的动态曲线段位在静态曲线分布最均匀的部分，以减少失真。当我们需要非线性检波或者利用非直线性来产生变频作用时，就相反地利用静态曲线较弯曲的部分。当我们想利用栅偏压的变动来自动调节音量时，我们便挑选那些I\(_{p}\)—Eg特性曲线弯折而拖着长尾巴的电子管（即远截流管）。特性曲线可以帮助我们解决的实际问题是这样多，而且熟能生巧用处更大。这方面的知识，可以说是我们无线电工作者和爱好者所必须掌握的基本知识。将来半导体大量代替电子管时，半导体也有特性曲线，原理仍然是相似的。（本刊参考张公绪、阎育苏两同志来稿编写）