电子计算机(图1)是应用无线电技术——电子学和脉冲技术的一种杰出成就,它能代替人的一部分脑力劳动,进行复杂的数学运算,解繁复的各种方程式,整理、分析和记录各种文件,控制自动化的生产过程以及把一种文字译成另一种文字。一部电子计算机需要上万个电子管,它的线路是相当复杂的。这里我们不打算把整个电子计算机的巧妙给读者做细致的分析,只想把一种数字电子计算机的各个组成部分的基本作用和它的两个重要组成部分——“计算器”和“存贮器”的工作原理,做一些通俗的解释。
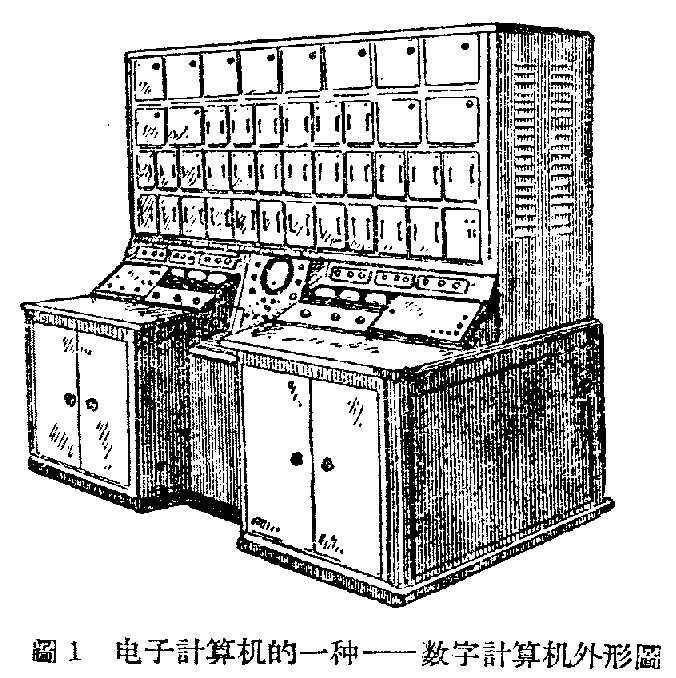
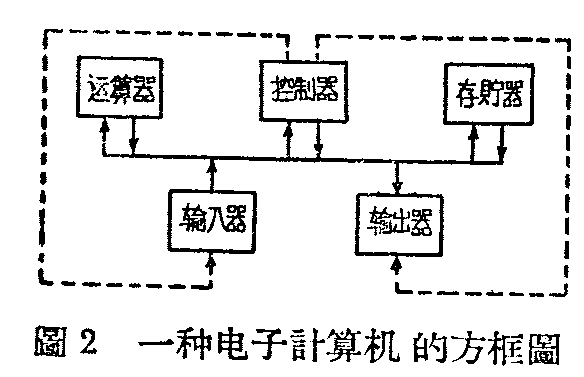
图2是一种电子计算机构造的方框图,它有5个主要部分:“输入器”、“控制器”、“存贮器”、“运算器”和“输出器”。电子计算机无论多么巧妙,还得有人根据所要计算的问题,供给它计算资料,为它安排好计算程序。人把需要电子计算机计算的具体要求和步骤提出来,写在“演算程序单”上,放进计算机去,它就能完全按着人的意图,进行一系列的演算,并求出最后的结果。在这“演算程序单”上有四项资料:(1)参与一定演算程序的数字,(2)进行加、减、乘、除那一种运算,(3)运算的先后次序,(4)计算过程中所获得的中间计算结果应当怎样在机内存贮起来,以便得到最后的结果。这些都是人对计算机的“语言”、当“演算程序单”放进“输入器”后,“输入器”就把人的“语言”译成直接命令电子计算机工作的“语言”。因此,人把“演算程序单”。一准备好,人的工作就完了。一个人在做一般的计算时,他总得拿起一支笔,用他的头脑,指使手动作,在纸上写下运算的各个程序的结果。这支笔就是“运算器”;人的头脑就是“控制器”,它发出各个运算细节的指令;那张纸就是“存贮器”。电子计算机也是这样。“演算程序单”经过“输入”后,就都存放在“存贮器”中,就像人先把题目写在纸上一样。按照程序的安排,那些就要参加运算的数据便在“控制器”的控制下进入“运算器”,控制器并按照安排的顺序,控制加、减、乘、除运算的步骤。就像控制器是在经常给计算器发出命令一样。计算器算出的结果,控制器又根据程序的安排,把它转入存贮器。准备以后和另一计算结果再一同送到计算器进行某种运算。当演算全部完毕后,控制器便按照安排的程序,使输出器工作,把存贮器里的最后结果译成人的“语言”,用打字机直接打在纸上。这就是一部电子计算机的主要工作情况。
倍增进位法
这里我们不来谈那些巧妙的利用光电效应,把演算程序单译成一系列的可以让电子计算机懂得的数据和指令的程序,也不详细说明这些数据和指令按一定位置被存贮起来,就像一大群蜜蜂进入一个个小洞的蜂房里的情形,和控制器怎样可以根据被存贮起来的指令的安排,把个别蜜蜂从蜂房里挑出来,搬到计算器又从计算器把结果搬到存贮器,最后又搬到输出器的情形。我们只来谈大家特别感到兴趣的计算器的基本演算是怎样完成的。为了要说明这些情形,我们首先需要了解电子计算机里所用的“倍增进位法”。
倍增进位法是逢一倍就进位的计数方法。在我们所习惯的十进位中,需要用1、2、3、4、5、6、7、8、9、0十个符号来把一些数记录下来,几个小于十的数加在一起满了十才进一倍。例如7+3的和满了十,就进一位写成10。在倍增进位制中,只需要用0和1两个符号来记录一切的数,1+1等于2,但不用“2”的符号来表示,而进一位写成10,四写成100,余类推。表一是倍增进位制中表示一些数目的写法:
表一
倍增进位 0,000,000 0,000,001 0,000,010 0,000,100
法数字 零 一 二 四
0,001,000 0,010,000 0,100,000 1,000,000 余类推
八 十六 三十二 六十四
举例来说:7=4+2+1,应当写成100+010+001=111。把64这个数用倍增进位制写出来就成了1,000,000。看起来好像很复杂,其实由于只用“1”和“0”,可以表示一切的数,使机器的工作大大地简化了。在电子计算机里,我们用一个负值的脉冲电压表示“1”,没有脉冲电压表示“0”。
在倍增进位制里,负数的表示法和正数相反,就是正数里的1写成1,而负数里的1则写成0;正数里的0写成0,而负数里的0则写成1,而且在负数末尾还加一个1。为什么这样表示负数呢,请看一个任意的计算例子:15-9=6。用倍增进位制来写15是01111,写+9是01001,写-9就是10111。假设我们在没有能够写下10111以前,先用abcde来代表。那么15-9就相当于01111和abcde相加,相加的结果应当是00110(即6)。
十进位 +15 倍增进位 01111
- 9 +abcde
———— ————
+ 6 00110
因此, e+1=10,∴e=1; d+1+1(由进位得来)=11,∴D=1;C+1+1(由进位得来)=11,∴C=1;b+1+1(由进位得来)=10,∴B=0; a+0+1(由进位得来)=10,∴a=0。因此,abcde应当就是10111。这样,减法在电子计算机里是用加法来计算的。
乘法是连续的加法。而除法是连续的减法,结果加、减、乘、除这4种基本运算都是用加法来完成的。
加法电路
数字计算机的加法电路是由两个“半求和器”和一个暂存器构成的,见图3。半求和器有这样的特性:当A、B端上同时有负脉冲输入时,进位端便有负脉冲输出。如果只在其中一端上有负脉冲输入时,总和端便送出负脉冲。若两端都没有脉冲输入,总和端和进位端也都没有脉冲输出。
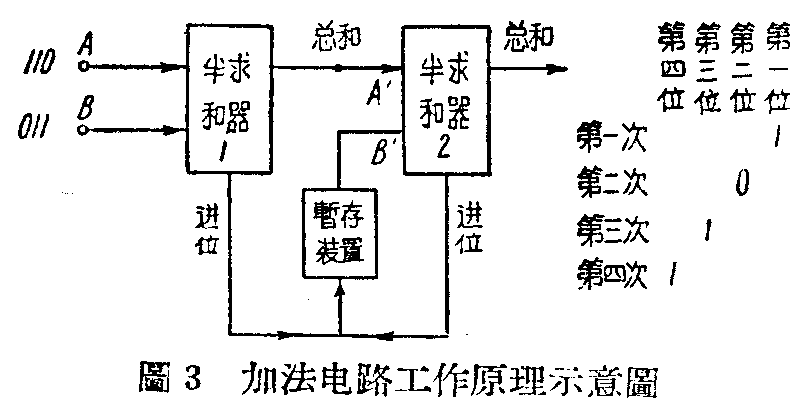
设我们要求6+7=13,这时相加的两串数码是110(6)111(7),加在半求和器A端的第1位数码是0,加在 B端的数码是1,就是说 A端没有负脉冲输入,而B端有负脉冲输入,结果半求和器1的总和端便有负腑冲输出。这个脉冲加在半求和器2的输入端A′上有负脉冲输入,B′端没有,所以它的总和端输出一个脉冲,因此记录在存贮器的第1位上的是1。隔一微秒钟后第2位相加,这时相加的数码都是1,即 A、B端都有负脉冲,因而有负脉冲由进位端输出,存放在暂存装置中,而半求和器2的两输入端均没有脉冲,因此无输出,于是记录在存贮器第2位上的是0。这一微秒钟后,才由暂存装置输出一负脉冲加到第2半求和器的B′端。当暂存装有一负脉冲输出加到B′端的同时,加在A、B端的是第3位的两个负脉冲(1+1),半求和器1的进位端又送出一个负脉冲到暂存装置,而在总和端没有输出,所以A′端没有输入,因此,半求和器2的总和端有脉冲输出,记录在存贮器第3位上的是1,再隔三微秒钟,数码没有了,暂存装置又有一次负脉冲输出到B′端,半求和器2又有输出,记录在存贮器的第4位上的又是1。总的记录是1101(即13)。
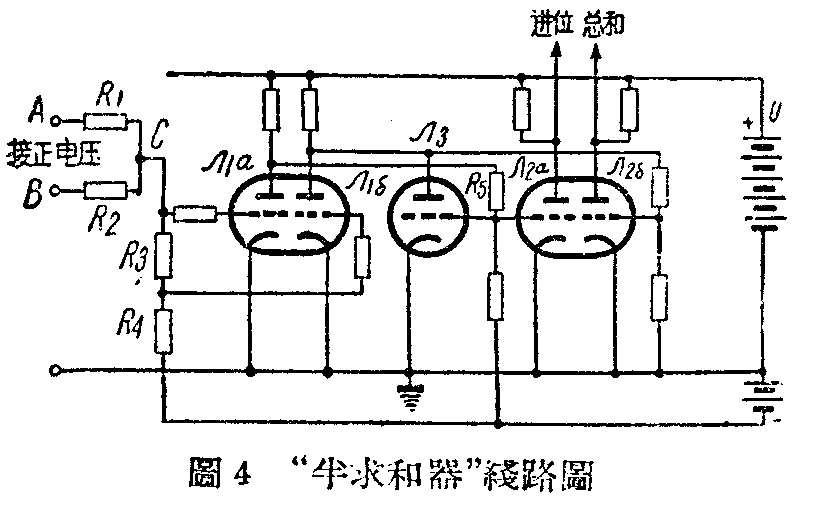
电子管构成的半求和器
图4是由两个双三极管和一个三极管构成的半求和器。在没有脉冲输入时,Л\(_{1a}\)、Л10的栅极处于正电位,都导电。Л\(_{2a}\)、Л20的栅极处于负电位都被截止,总和端和进位端的电压等于屏极电池的电压+U(实际机件上并不是用电池充电源)。在1+0的情况下,A端有负脉冲输入,B端没有,C点的电位便下降到某一数值,使Л\(_{1a}\)的栅极电压还不能截断屏流,而Л16的栅极接在R\(_{3}\)、R4间,更接近-U处,有了足够截止屏流的负压。这时,Л\(_{15}\)的屏压上升,使Л25栅极的电压趋正而导电,于是总和端的电压下降,即有表示1的负脉输出。由于Л\(_{2a}\)不导电,进位端没有脉冲输出。在1+1的情况下A、B端都有负脉冲输入,C点的电位下降得更低了,结果Л1a也不能导电,Л\(_{1a}\)的屏压立刻上升,并经过R5而加在Л\(_{2a}\)和Л3的栅极上,抵消它们的负偏压,使它们导电。Л\(_{2a}\)导电,进位端电位便从U突然下降,即有负脉冲输出,而Л3的导电却把Л\(_{1a}\)的屏压短路接地,因此Л20不能导电,总和端没有输出。
磁性暂存袋——磁鼓
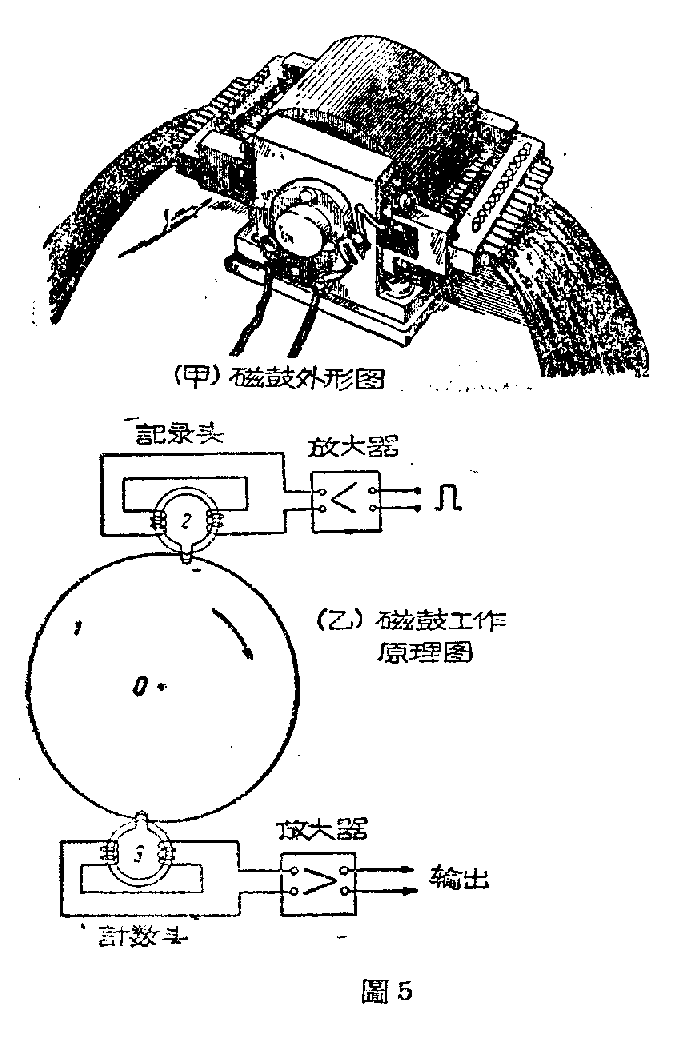
存放进位脉冲的磁鼓的构造如图5所示。它有两个放大器、一个记录头、一个计数头和在记录头间隙中及计数头间隙中迅速旋转的磁带。记录头和计数头都是一个具有间隙的环形铁心,其上绕有激磁线圈。当脉冲电流通过激磁线圈时,在铁心的间隙间便产生磁场,使极小的一段磁带磁化。通常在每公分上能记录40个脉冲。磁带绷在迅速旋转的圆鼓上,约以经1微秒后,被磁化的那部分磁带便转到计数头。当被磁化的磁带通过计数头时,在记数头铁心的线圈里就感应出脉冲电压。这个脉冲电压被放大后送进半求和器2的B′端。这样磁鼓就把进位脉冲存贮一个极短的时期——1微秒,然后再送出去。此外,磁鼓还能记录运算的数据、演算的结果以及控制器的命令等等。(本刊根据汪国兴稿和朱邦俊译苏联技术科学博士φ、B.马欲洛夫著“电子计算机”稿编写)。