本刊第8期所载安绍萱“超外差式收音机是怎样工作的”一文,解释混频作用过于简略,对如何产生中频的物理过程会使读者发生误解,本文专谈“差拍”和“混频”问题,藉以回答关于安绍萱文章读者所提出的疑问
——编者
“差拍”和“变频”是有着本质上的区别的两个物理过程,但是常常不小心就把它们混为一谈,使我们对无线电里的一些问题,产生了错误的理解。
简单的说:“差拍”并不产生新的频率,“变频”产生出新的频率来。这两句话,一下子很难明白,下面我们做一些浅显的解释。
先用声音的差拍作为例子来说明。
找来两只音叉,一只的振动频率是每秒1000周,另一只是每秒1003周。敲击第一只音叉,它就“嗡”的发出1000周连续的声音;敲第二只音叉,它所发的是1003周连续的“嗡”声。
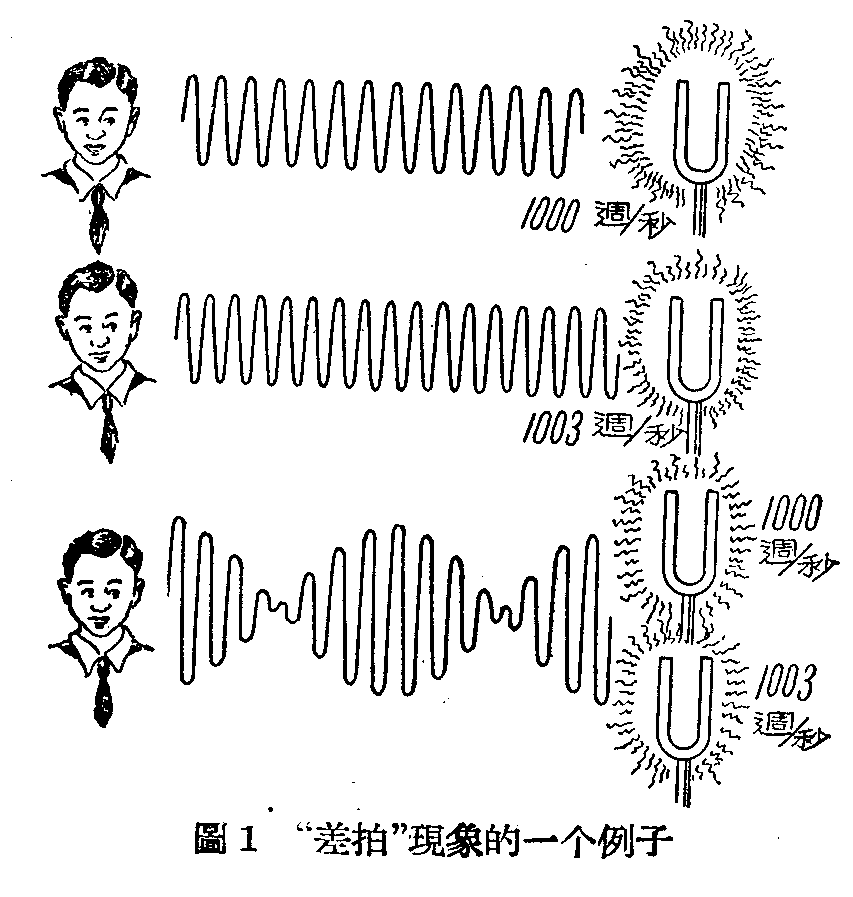
现在,同时敲击这两只音叉,我们所听到的就不再是连续的嗡声,而是一种有强有弱的“嗡——嗡——嗡”的声音,每秒钟三次,恰好等于两个音叉频率的差。这种现象,就是所谓“差拍” (图1)。
但是,如果你因此就说:“我听到了每秒3周的声音”,那就错了。因为人的耳朵是听不见每秒3周的声音的。再说,这里根本没有每秒3周的新频率产生出来。
另外再找两只“音叉”,一只的振动频率是每秒20000周,一只是每秒21000周,做同样试验。请猜想:我们能否听到21000-20000=1000周的声音呢?如果这时产生了1000周的声音的话,人的耳朵是可以听见的,但事实上你将什么也听不见!这是因为20000周以上的振动,人们根本听不见的缘故。
这些试验,充分说明两个频率的振动直接相加,是不会产生出新频率来的。
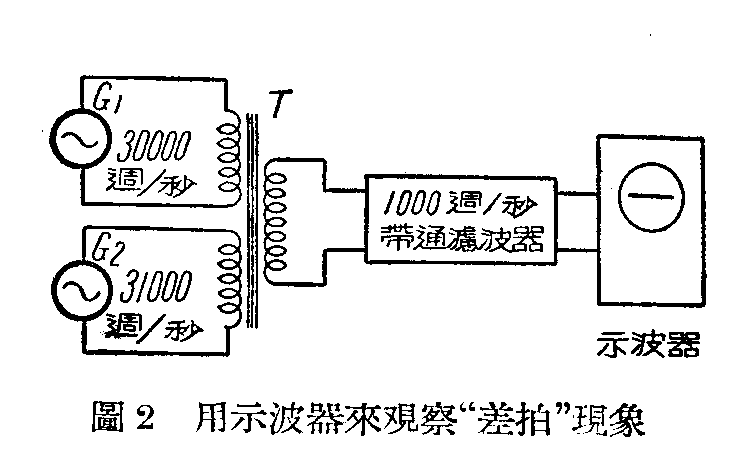
上面举的是声音振动的例子,电的振荡也是这样。把20000周和21000周的两个电压波如图2那样直接加起来,经过一个1000周的带通滤波器(意思就是单单把1000周取出来),再接到示波器上,我们会看不见1000周的波形。示波器的萤光幕上分明还是一条横线,和没有接什么东西上去的情形完全一样。
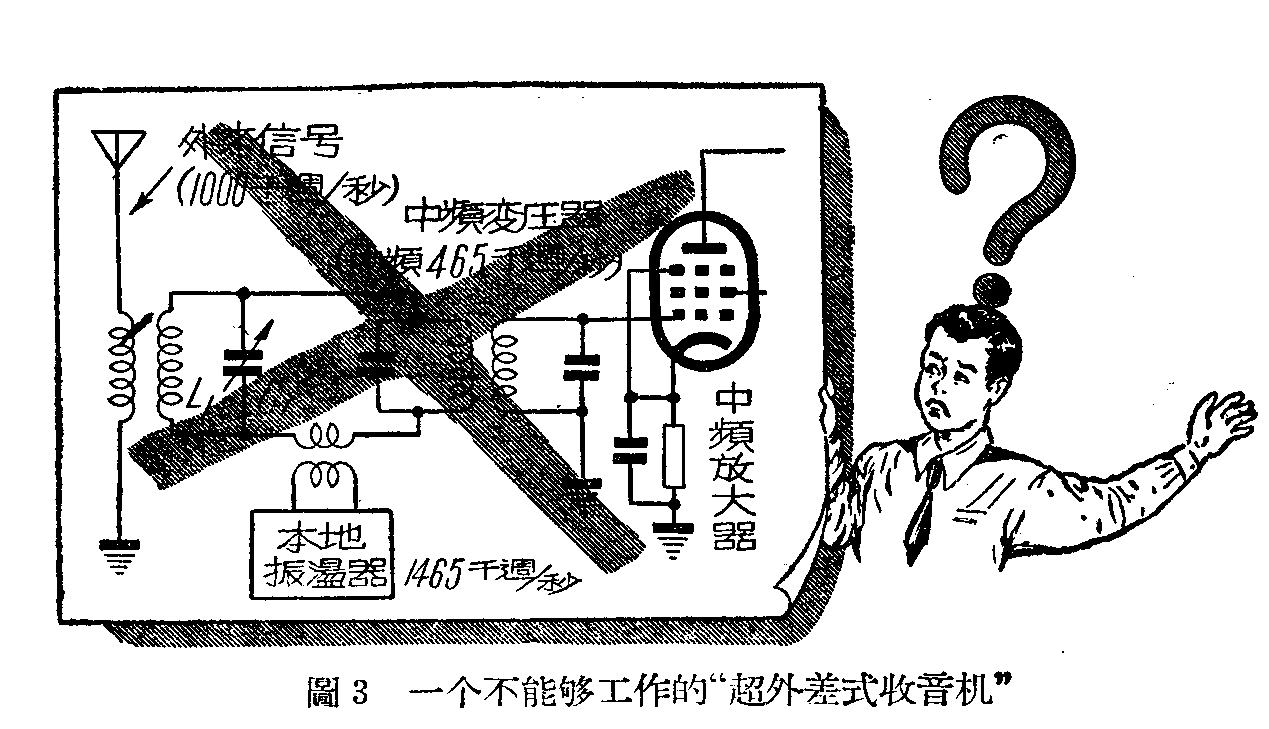
我们不妨假想有人装了一部像图3那样的“超外差”式收音机,事实会告诉我们,这个“收音机”是不能收音的。假如外来信号是1000千周,本地振荡器的频率是1465千周,它们叠合起来,虽能产生每秒465000次有强有弱的差拍变化,但线路中仍旧只有原来的1000千周和1465千周的电振荡。线路里的中频变压器只选择465周的电振荡,其它的频率实际上都会被它滤掉,结果在中频放大器的栅极上一点信号电压也没有。这样一部“超外差”式收音机是不可能有的。
那么,究竟怎样才能得到465千周的中频呢?要回答这个问题,让我们先来谈谈“直线性元件”和“非直线性元件”的区别。
“直线性元件”这个名词很陌生,其实它所指的是件顶普通的东西。在无线电里,任何东西如果它的电流和加在它上面的电压成正比例的,都是这种“元件”。例如电阻器、电容器、空心线圈、放大后的电子管等,都是“直线性元件”。
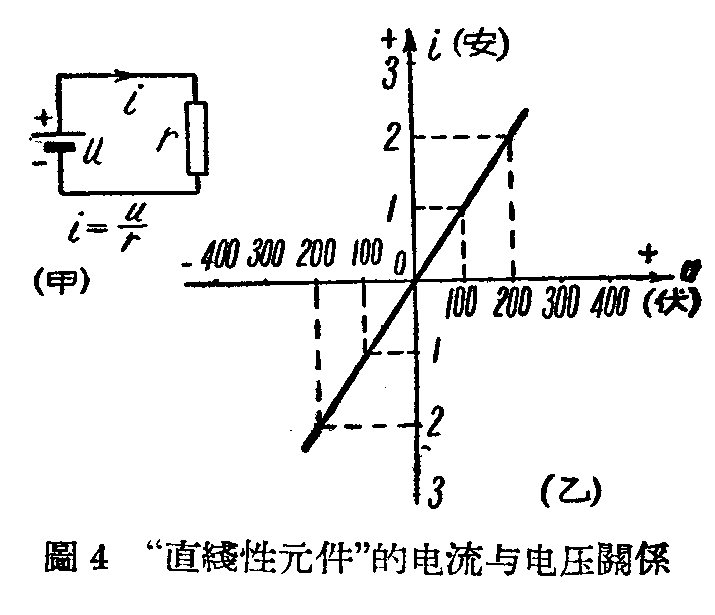
拿电阻来作例子。当有电压u和在一个100欧电阻上面时,产生的电流i如图4甲。u等于100伏,i等于1安;u等于200伏,i等于2安;电压增加多少倍,电流也增加多少倍。这也就是我们很熟悉的欧姆定律所表示的关系。而且,把电压u的方向调换一下,电流i动的方向也同样调换。如果我们给一个u-i曲线图,采用i做纵坐标,u做横坐标,所得到的将是一条笔直的直线(图4乙)。
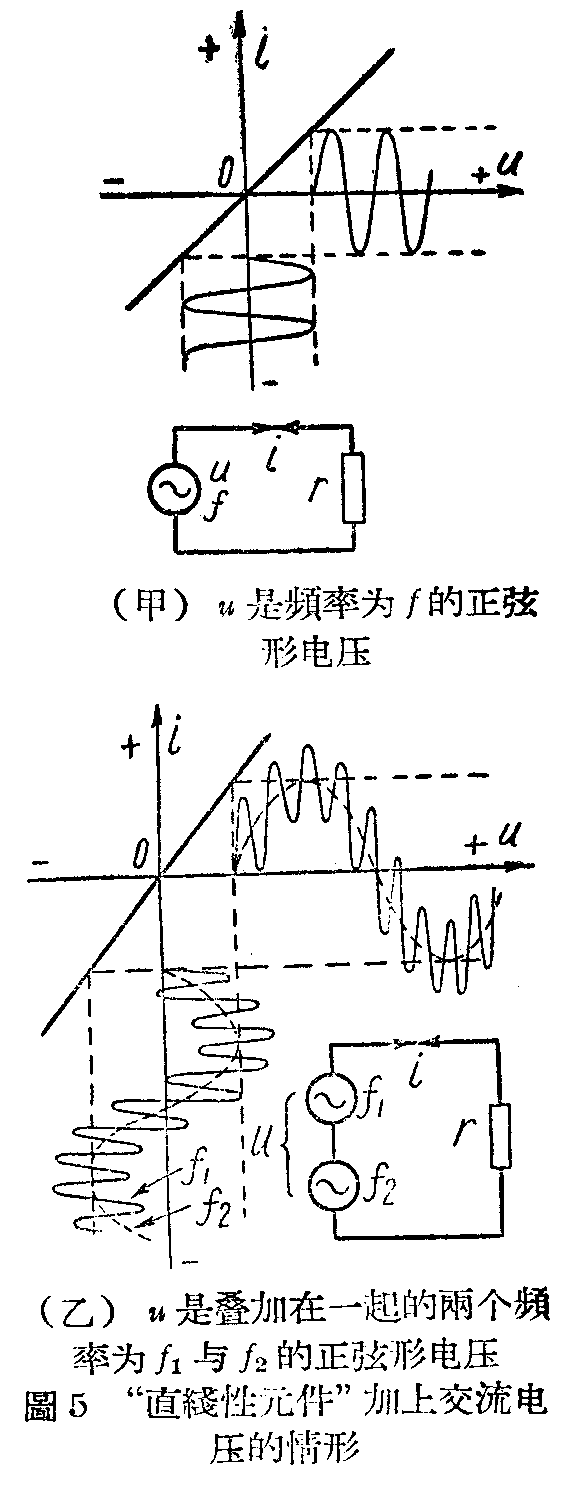
我们可以看出:如果加在“直线性元件”上面的电压u是一个频率为f的正弦波形交流电压,那么所得到的电流i也会是一个频率为f的正弦波形交流电流如图5甲。
如果加在“直线性元件”上面的电压u。是叠加在一起的两个不同频率的正弦波交流电压。那么所得到的电流i也是叠加在一起的两个同样频率的正弦波形交流电流如图5乙。
这是“直线性元件”的特性。
可是“非直线性元件”就有大不相同的特性。通过“非直线性元件”的电流,和加在它上面的内压,关系比较复杂,不是成简单的正比例的关系。常见的矿石检波器、氧化铜整流器和混频级的电子管,都是非直线性的元件。
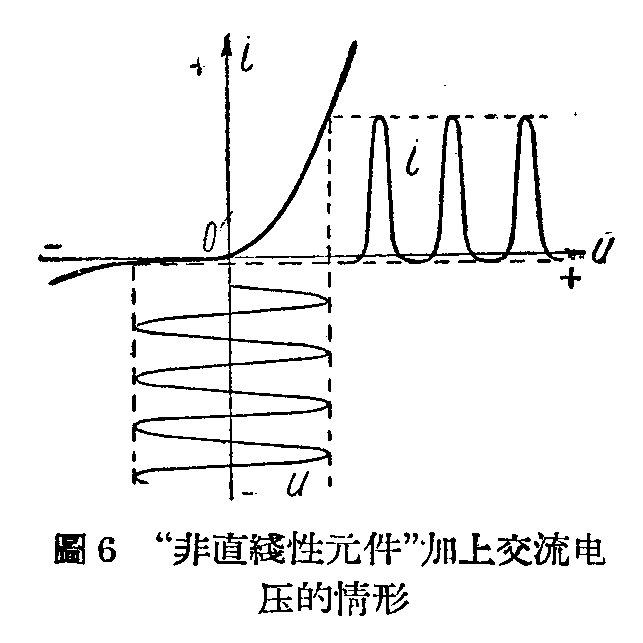
如果我们用上面所谈过的办法绘出非直线性元件上电流和电压的关系图,可能得到像图6那样的曲线。从图6显然可以看出,加上去的电压u是正弦波形,而得到的i是一个被“歪曲”了的奇形怪状的波形。如果“直线性元件”是一面平面镜子,“非直线性元件”就好像一面“哈哈镜”,本来是端端正正的模样,却被照成怪头怪脑的形像了。
那么,这种被“歪曲”了的、奇形怪状的——或者按术语说非正弦波形的——电流,又起什么作用呢?
在无线电里,我们并没有因为“非直线性元件”的表现不真实而抛弃它;相反的,我们就利用它来产生新的频率。
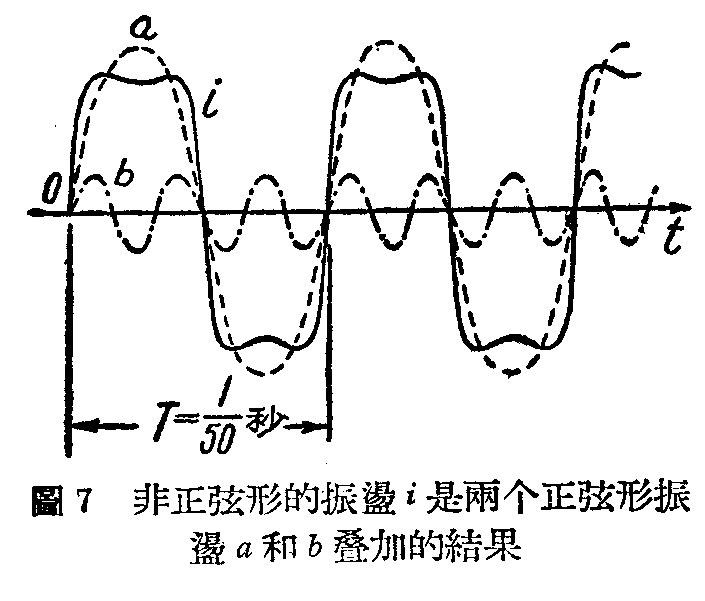
假设我们产生了一个非正弦波形的电振荡1如图7,我们很容易看出它实际是两个正弦波a和b相加的结果。b是a的谐波,如果a的频率是f,b的频率就是3f。所以只消把原来的正弦波“歪曲”一下,“压扁”它或“切掉”它的一部分,使它变为非正弦波形,就可以“制造”出新频率来。
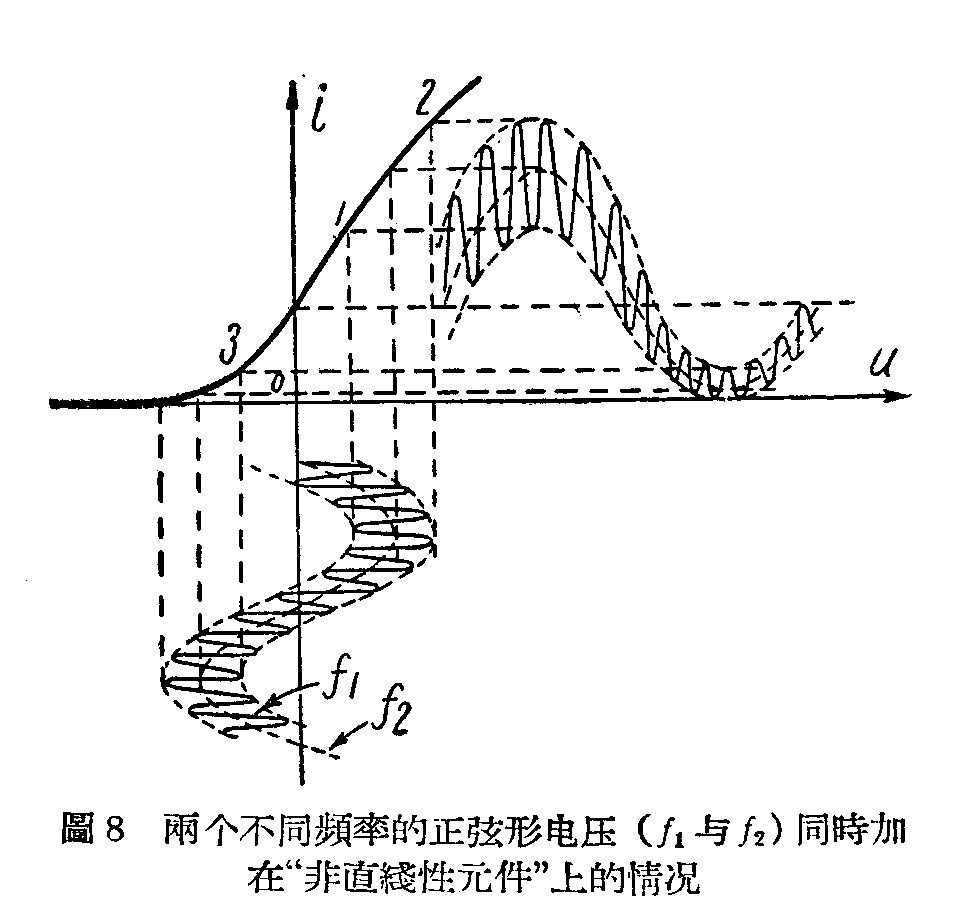
倘若我们用两个正弦波形电压u\(_{1}\)和u2,一个频率是f\(_{1}\),另一个是f2,同时加在“非直线性元件”上,又会产生什么结果呢?自然,所得的电流中会出现f\(_{1}\),2f1,3f\(_{1}\)……和f2,2f\(_{2}\),3f2……等频率。此外,u\(_{1}\)叠加在u2上以后(图8),所得的电流,不仅随个别电压作非直线性关系的变动,到底是怎样一种变动法,还要由两电压的和所得的工作点所决定。我们看在图中1、2、3三个工作点上,电流随电压而变动的情形是各不相同的。换句话说:在非直线性元件上,两个电压所产生的效果不是彼此独立的,而是相互影响的。结果,除了产生上面所说的f\(_{1}\)、2f1、3f\(_{1}\)……和f2、2f\(_{2}\)、3f2……等新频率外,还会产生f\(_{1}\)+f2,f\(_{1}\)-f2,2f\(_{1}\)+f2,2f\(_{1}\)- f2……等新频率。
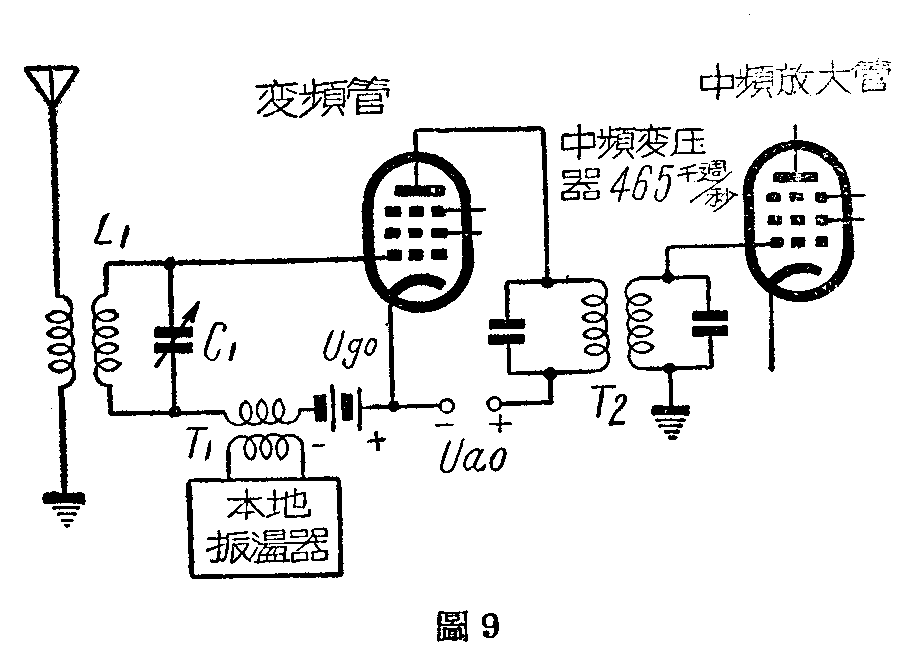
在超外差式收音机里,一个1000千周的信号频率电压(相当于f\(_{2}\))和一个1465千周的本地振荡频率电压(相当于f1),同时加在“非直线性元件”的混频级的电子管的栅极上如图9,能够产生1465-1000=465千周的中频来,就是因为其中有“f\(_{1}\)-f2”的新频率出现的缘故。简单的说,这是“频差”;但这绝不是“差拍”。混频级的输出接到一个中频调谐回路,专门选择465千周,所以能够产生中频放大,增加收音机的灵敏度。(古吉 田弓)