电容器是无线电的重要零件之一,它的基本形式是相对放着的两块金属片(如图1)。我们说它能“容电”,这是很容易用实验证明的。(如图2)把一个电池的正负两极经过开关分别接到电容器的两个金属片上。在开关没有合上以前,这两个金属片和普通的金属片一样,上面是没有电的。但一合上开关,接电池正极的那个金属片上就带正电(缺少了电子);另一片上就带负电(有了多余的电子)。若把开关再断开,把电容器的两根接线相互碰一碰,在接触处就会冒出火花来(图3),这分明就是电容器已经容有电而且正在放电的现象。
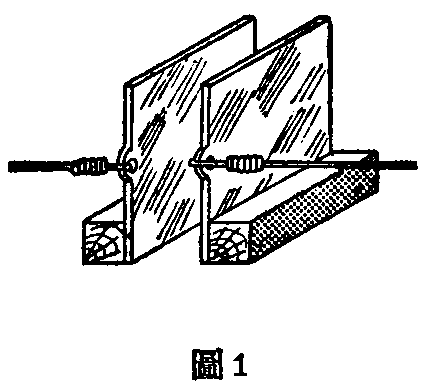
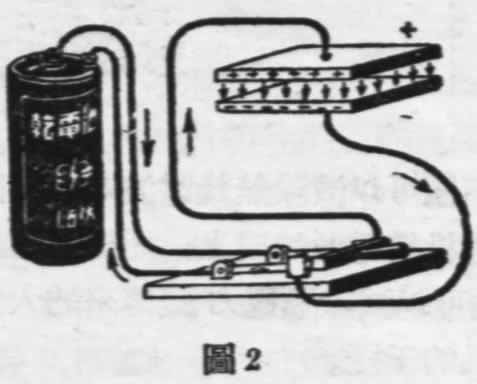
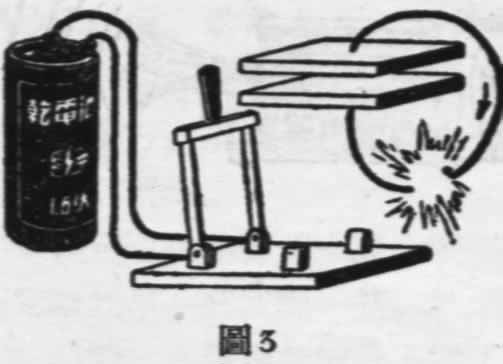
电容器能够容电的道理是这样的:电池的正极缺少电子,一接通金属片,那块金属片里的自由电子就通过联接线和开关跑到电池的正极去,原来不带电(金属的原子是中和的)的金属片,因此就显出有正电荷来;电池的负极所多余的电子,又会相互的推开,经过导线和开关推到金属片上去,结果是金属片带有负电荷。所以电容器能够容电,是电荷同性相斥异性相吸的结果。让电容器带电的上述过程,我们叫做“充电”。
但是这些电荷到底存在于电容器上的什么地方呢?我们晓得两个金属片是相对的放置着的,一带正电,一带负电,会相互吸引,把电荷都拉到彼此相隔最近的地方去,所以金属片上的电荷是都集聚在那相对的表面上(图4)。
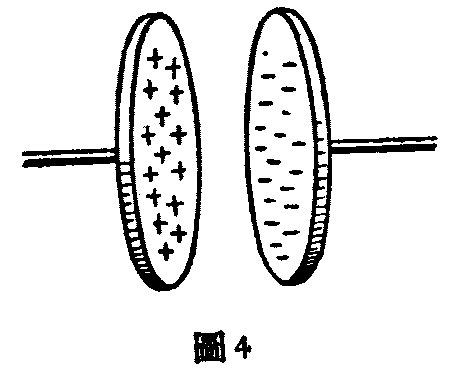
自然,增加电池的电压,即正极缺少更多的电子,负极多余更多的电子,便可以把电容器充到更多的电荷。因为这时的电池的正极,对电子有更大的吸力,而负极对电子又有更大的斥力。但另一方面,带负电荷的金属板,对带正电荷的金属板上的电子也有斥力,使电子容易跑到电池正极去,等于增加了电池电压的作用一样;相反的,带正电荷的金属板对带负电荷的金属板上的电子有吸力,使电子容易由电池负极路过来,也等于增加了电池的电压的作用一样。所以电容器能够被充电,必须要有电源;但到底能充上多少电,不仅决定于电源的电压,还决定于电容器的构造,也就是两金属片的相互关系位置。它们隔得近,相互吸力大,充电就多;反之,充电就少。
谈到电荷之间的吸力,我们过去还没有注意到一个事实:就是同样的两个电荷放在空气里和放在水里或油里,相互之间的吸力是各不相同的。换句话说:电荷之间的吸力或斥力,除了和电荷的大小及相互距离有关外,与电荷之间的介质(介于二者之间的物质)也有关系。因此,电容器的两金属片间,如果用了不同的介质,两金属片的电荷,就会有不同的吸力,充起电来,就会得到不同的电荷。
一般绝缘物质如空气、油、纸、云母或电解液体等,都可以用做介质,电容器因介质的不同种类也繁多,用途也各有不同,我们就分别叫做空气电容器、油质电容器,纸质电容器,云母电容器和电解液电容器。而这都是常用的几种电容器如图5。
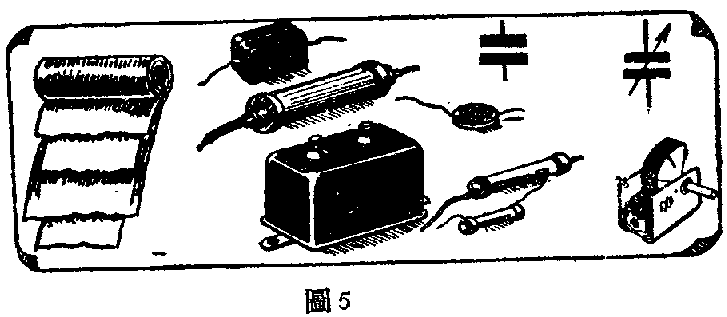
电容器的电容量
为了说明一个电容器的容电性能,我们习惯地用它的“电容量”来表示。就是表示在外加电压为一固定数值的情况下,它能够容多少电荷的意识。在M.K.C.单位制里,电容量的单位为“法”。设外加电压为E伏,它能充电得到电荷Q库,那么这电容器的容量C就是:
C=\(\frac{Q}{E}\)法
也可以说:电容量等于用每单位电压充电所能得到的电荷数。很显然的,这里所说的电荷,是指金属片一片(或一组)上的电荷。两个金属片一片(或一组)是储正电荷,另一片是储相等的负电荷,正负互相抵销,实际上它们的储电总量是永远等于零的。
根据上面的分析,我们知道电容器的电容量C应当和金属片相对的面积A(在这里电荷是真正的集聚着)的大小成正比,和两片之间的距离t成反比(距离愈小,吸力愈大,储电量愈大)。除此以外,它还和所谓“介质常数”K成正比。
“介质常数”是代表介质影响电容器容量的一种特性,它和介质的绝缘强度并不是一样的东西。在M.K.C.制里,真空的介质常数是1,空气的介质常数为1.00585,而云母的介质常数为7—7.9。换句话说,原来是空气的介质换上云母介质就可以增加电容量7—8倍。
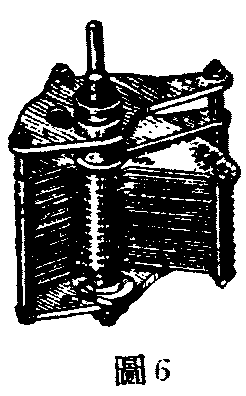
为了增加面积,可用许多金属体联成两组,然后把两组各片间都用一定的介质隔开使它们相对的平行的装牢(如图6)。这样做成的电容器的容量的计算式为:
C=0.0885\(\frac{K(N-1)A}{t}\)微微法
上式中,K为介质常数(空气的K=1.00585),N为两面总共的片数,A为每片的面积平方公分数,t为相邻两片间的距离公分数。C的单位为微微法,是因为实用起来,“法”这单位太大,1微法为\(\frac{1}{1000000}\)法,1微微法为1;1000000微法,而微微法是比较常用的电容量的原故。
我们必须注意,介质常数其实并不是固定不变的。它随着电流频率、潮湿程度、温度和外加电压不同而有变化。所以除了空气电容器外,其他介质的电容器,在高频工作时的电容量和低频时的电容量是不同的。
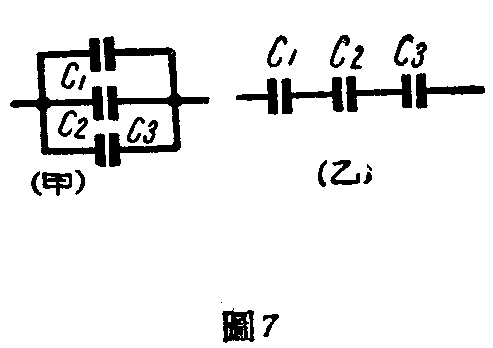
许多电容器并联(图7甲),等于把每一片金属片面积增大,所以电容量也增大。例如三个电容器的电容量各为C\(_{1}\),C2,C\(_{3}\)。那么,它们并联后的电容量CT即为:C\(_{T}\)=C1+C\(_{2}\)+C3。
许多电容器串联(图7乙),等于把介质加厚,所以电容量反减小。例如上述三个电容器串联后,C\(_{T}\)为:
C\(_{T}\)=11;C1+\(\frac{1}{C}\)\(_{2}\)+1;C3
举例:设两个电容器串联,C\(_{1}\)=20微微法,C2=0.002微法=2000微微法。即得:
C\(_{T}\)=11;20+
电容器在交直流回路里的作用
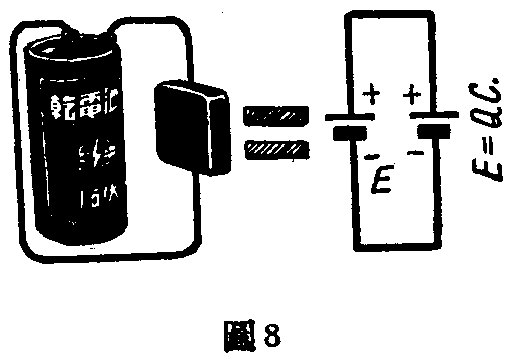
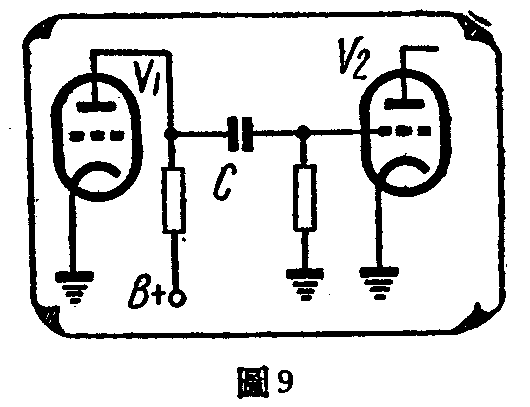
从上面所谈的电池对电容器充电的过程看起来,我们可以这样说:电容器对电流的通过是有抗拒作用的。刚开始合上开关时,电子迅速的由一个金属片跑到电池,并由电池跑到另一个金属片,电流是很大的。但瞬刻间电容器上有了电荷,电流就完全停止,这时电容器在回路里的作用,就相当于一个电池,只是和原来的电池电压相等极性相反的对接着,所以回路里没有电流(图8)。因此,电容器对电流的通过是抗拒的,而且对稳定直流的抗拒,相当于一个不通电流的开路,也就是相当于无穷大的电阻。正因为如此,无线电收音机里,时常用电容器把直流电压隔开,例如图9就是用了电容器C将电子管V\(_{1}\)带正电压的屏极和电子管V2带负电压的栅极隔开。这种用法,我们又叫做隔断电容器。
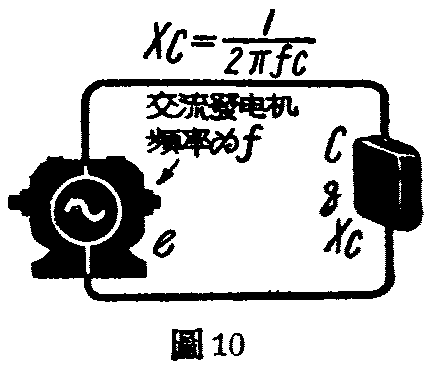
但在交流回路里(图10),电容器就不能完全隔断电流。由Q=EC式可以看出,当外加的电压变为交流电压时,金属片上所集聚的电荷量应当也随着变动,电压的变动愈快,电荷量的变动也愈快。换句话说,在仅有电容器的交流回路里,电流的大小和交流频率成正比,也就等于说电容器抗拒电流的作用是和交流频率成反比。此外,电容量愈大,电容器片上的电荷量也愈大。同样大小的电压变化,电荷的变化也愈大。这就等于说电容器抗拒电流的作用,是和电容器的容量成反比。
电容器对电流的抗拒作用,我们叫做“容抗”,它的单位和电阻的单位一样都是“欧”,常用X\(_{C}\)来表示。计算XC的公式是:
X\(_{C}\)=\(\frac{1}{2πfC}\)
上式中f为电流频率周数,C为电容量法数。当频率极高时,电容器的电抗极小,根本不能起多大的隔电作用。而对直流来说,因直流的频率为零,所以X\(_{C}\)为无穷大。
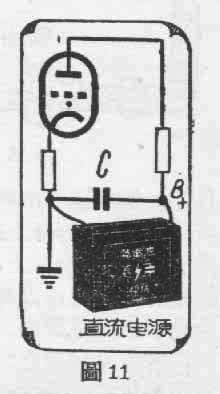
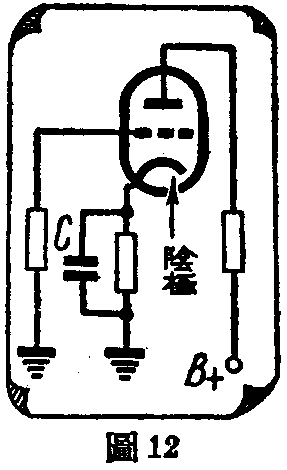
无线电里经常利用电容器不能抗拒高频而能隔断直流的特性,起着许多不同的作用。例如图9的隔断电容器又常叫做交连电容器,它可以把V\(_{1}\)管屏极上的交流电压的变动没有多大阻挡的传到V2管的栅极上。我们又时常在直流电源上并联一个电容器,使得高频电流完全经电容器畅通无阻,而不会跑到直流电源里去(图11)。有些电子管的栅极的电压,并不是专用直流电源供给,而是在阴极上串联一个电阻来供给的。这时如果在阴极串联的电阻上再并联一个电容器如图12,那末通过阴极的高频电流,就可以丝毫不受到电阻的限制,都可以从电容器方面通了过去。这样的用法叫做“傍路电容器”。
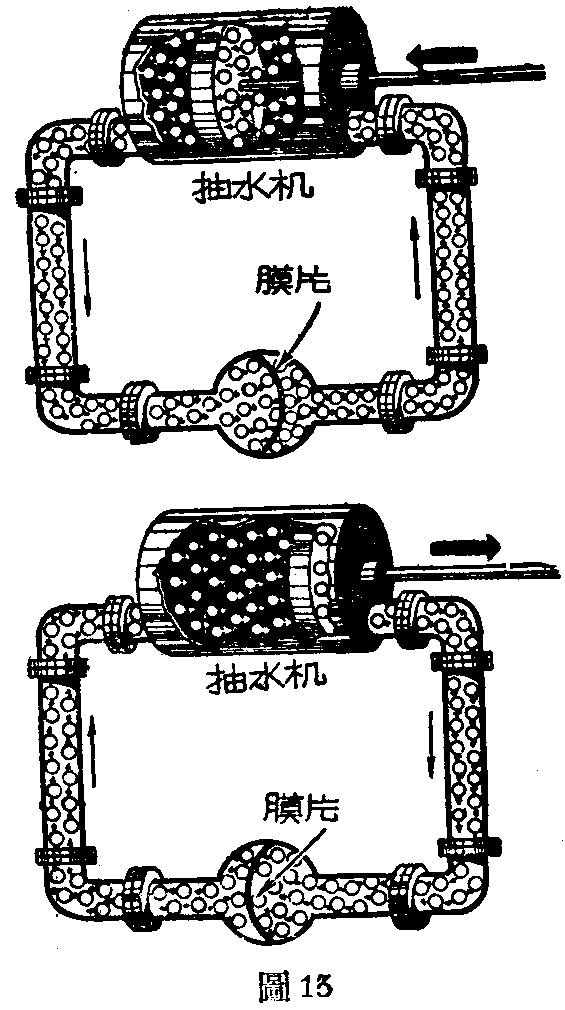
但是我们必须注意,电流通过接有电容器的回路,并不意味着真有电荷从电容器一个金属片经中间介质跑到另一个金属片上去,而是当一个金属片的接线上有电流流动时,另一个金属片的接线上一定也同时有电流流动,结果所有接线上都有电流流动,就等于电容器没有隔断交流的作用。这情形可以用图13来说明。交流电源相当于抽水机,电容器相当于一个有弹性的膜片。当抽水机不断来回抽动时,弹性膜片来回振动,两面水管子里的水都同时流动,但并没有任何水分子真正从弹性膜片一边通过膜片跑到另一过去。
实用电容器的常识
我们可以拿些实例,把电容器的使用方法做些具体说明:
(1)电容器的性能,一般是以电容量和工作电压来标示的,但大电容器还须标明电流,和相当于该电流的频率。
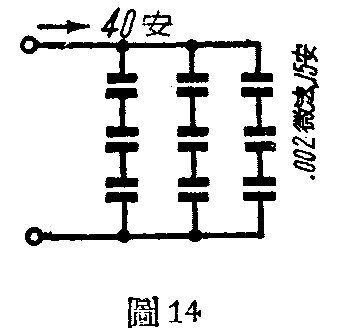
设在某一发信机的回路里通过的电流是40安,而为了使回路正常工作又要求在回路里接上一个0.002微法的电容器。但现成的电容器都只有 0.002微法和 15安的。于是设计工程师就用了9个这样的电容器接成如图(14)的样子。这样的接法,不仅符合了电流和电容量的要求,还使每个电容器的电压减为总电压的三分之一,不容易将介质打穿。
设工作频率为200千周,图(14)这一组电容器的容抗X\(_{C}\)是:
X\(_{C}\)=\(\frac{1}{2πfC}\)=1;6.28×200000×0.002/1000000=398欧
X\(_{C}\)两端的电压应当是电流和XC的乘积即等于40×398= 15920伏,那么,每个电容器上的电压就是\(\frac{15920}{3}\)≈5300伏。这样用10000伏和0.002微法的电容器已经很安全。这比用一个 0.002微法30000伏的电容器还要经济得多。
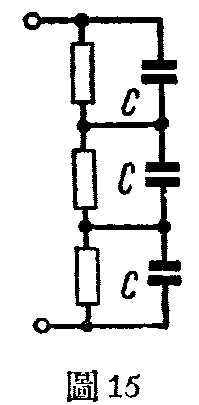
(2)当用几个大电容器串联作滤波器时,恐其中之一有漏电现象,影响每个上面的电压分配,把其余的电容器打穿,我们常常需要用几个电阻和电容器并联如图15。
这两个例子都说明发信机里的大电容器的使用,要多考虑到安全装置问题。我们一方面怕介质因电容器过高而打穿,损坏了电容器和有关的回路;同时我们还须考虑到经过电容器的电流量是否超过额定数值,因电容器两端的电压为IX\(_{C}\)=\(\frac{I}{2πfC}\),可见额定电压和额定电流之间有相互的关系,频率愈低,为了不超过额定电压,电流应当减小。
收信机里,电压小的地方多用纸质电容器,电容量约在0.05—4微法之间;不应当有丝毫漏电的地方,常用云母电容器,容量较小,一般不超过0.05微法。在高频和中频回路里用的傍路电容器,一般是0.05—0.1微法;在音频里的傍路电容器,一般是0.25—1微法。栅漏检波回路上常用0.00025微法;高频级间交连常用0.0001微法,音频级间交连常用0.01—0.25法。一个好电容器用欧姆电表量出来的电阻每一微法应不小于50兆欧,例如10微法的电容器应大于5兆欧。
收信机里常用的电解电容器,分干湿电解液两种。一般整流滤波用的多是4—8微法,电压为400—500伏。音周傍路多用10—50微法,电压为25—25伏。灯丝电源(直流供给)滤波器里的电容器,常用1000—2000微法,电压为15伏。这种电解电容器的漏电电流,每微法不应超过0.25毫安。
一般可变电容器,系以最大电容量为额定值,通常用在调谐回路或充配整及垫整电容器。
这些种不同的电容器和它们的使用方法,在我们分析收信机回路时,再详细解释。(沈肇熙)