线圈

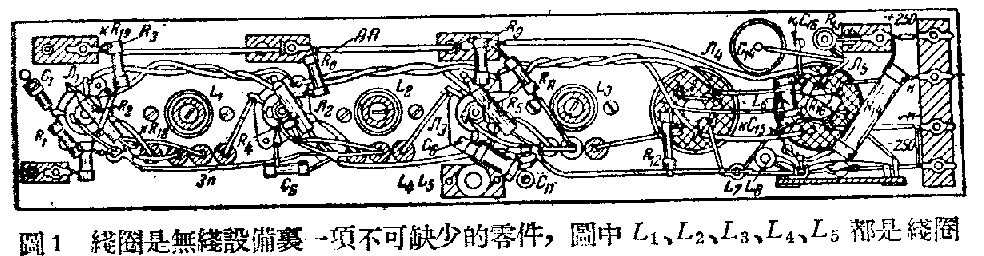
打开任何一种无线电机器来看，除了电子管外，里面主要的零件有三种，就是：电阻器、电容器和线圈。要紧的线圈少了一个或甚至联接得不够好，整部机器就完全可能失去效用；一般的线圈省去一个不用，也往往严重地影响到机器工作的质量。所以线圈的基本作用，很值得我们注意。

正像电池是“电源”一样，通着电流的线圈就是“磁源”。线圈性质，过去我们解释的，还只限于电流是稳定不变的直流一种情况（本刊第六期），如果通过线圈里的电流是交流，方向和大小在不断地随时间变化，像变压器里的电流那样，这时的线圈还起什么更多的作用呢？自然，电流变化，线圈里通过的磁力线也去跟着变化；过去，在谈电磁波的来源的时候，我们也曾经介绍了有名的法拉第的发现，就是：如果通过一个线圈里的磁力线有增减时，在线圈的导线里会产生电动势，把这线圈两端经电表接通，这时便看得出线圈里有了电流。

对这些现象，俄国的科学家楞次做了最初的解说，因此他的解说，现在就叫做楞次定律。

楞次定律，不把线圈对电流的关系，当着是基本关系。而把线圈对变动磁力线的反应看成是线圈的基本特性。因为线圈对通过它的磁力线的任何变化，如一块磁铁的伸进拉出，或受另一个线圈所发生的磁力线的影响的忽大忽小，或由于线圈本身电流的变化所引起的磁力线变化，反应的规律都是一样的。楞次定律经过无数次试验所证明，可写成下面一句简单的话：

“当通过一个线圈里的磁力线有变动的趋势时，线圈就有维持那通过的磁力线不变动的趋势”。

用这规律，我们可以说明许多问题。

例如一个变压器，当它的初级线圈里有交流电流时，初级线圈发出的磁力线能够通过次级线圈的数量就会随电流变动，因此按照法拉第的发现，次级线圈里一定会“感应”出电动势来，为的是有可能在次级线圈里产生电流，这电流又产生相反地磁力线变动，使得通过次级线圈的磁力线有维持不变的趋势。因此我们说线圈虽是“磁源”，但它同时还有抗磁作用。

又例如将一个电池经过开关接到线圈时，开始通过线圈里的电流及这电流所产生的磁力线有增加的趋势，这时按照法拉第的发现，线圈里一定会产生一个反对电流增加的电动势，有了这个电动势，就有可能在线圈里产生相反的电流和磁力线，有阻止电流增加，因而维持通过这线圈的磁力线数量不增加的趋势。因此我们又说“线圈”有“电抗”作用，这电动势虽不是什么直接的电源，但它是一个“感应的电源”。这里线圈“抗磁”作用的实质表现为了“电抗”，我们可以说“电抗”作用是“抗磁”作用的一种特殊表现。

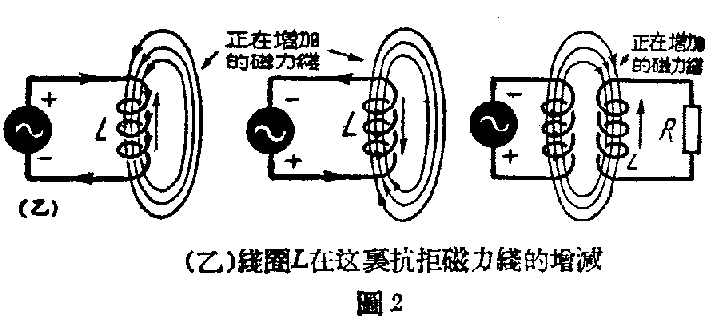
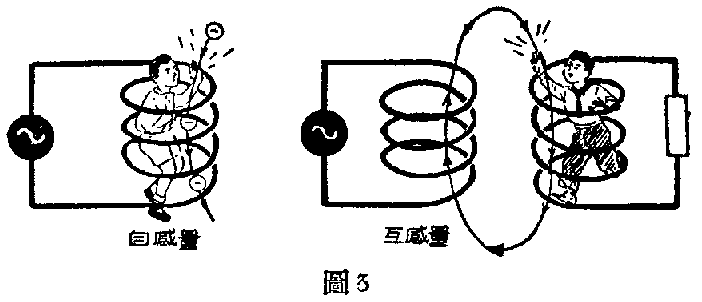
因为这种抗拒作用，都是靠在线圈里先“感应”出电动势，而这电动势又产生电流来完成的，所以我们说线圈是有“电感量”的。“电抗”作用，是抗拒线圈自身电流的变化，我们说线圈有“自感量”；“抗磁”作用，若是阻止另一线圈所发生磁力线的通过，我们说这两个线圈之间有“互感量”。

从上面的说明，我们看出一般线圈对通过它的磁力线的变化，是表现了“惰性”的；它对通过它的导线里的电流变化，也是表现了“惰性”的。这磁力线或电流要变化，线圈不让它们变化，因此这种变化只能逐渐完成，不能立刻完成。在上面把电池经过开关接到线圈的例子里，线路接通时，线圈里的电流是逐渐上升的，而将线路断开时，线圈里的电流又是逐渐下降的，这时在开关处所发生的火花，就说明电流还在继续流动。

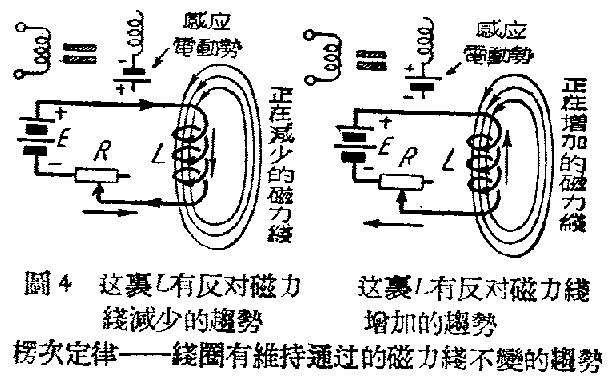
楞次定律——线圈有维持通过的磁力线不变的趋势

这在振荡回路里就利用这种惰性产生振荡，这是无线电发信机里最重要的一部分；在谐振回路里产生谐振，表现出放大能力和选择性，是收信机里最重要的一部分。在滤波回路里，阻止高速度变化的电流成分，而保留变化较慢的成分，使得我们可以由交流得到直流，或使得不同频率的电流各走各的路，不致相互混杂。

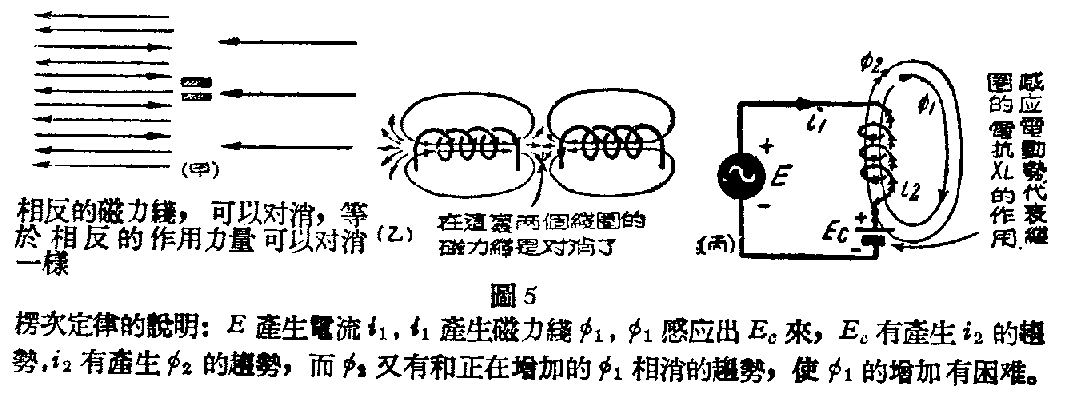
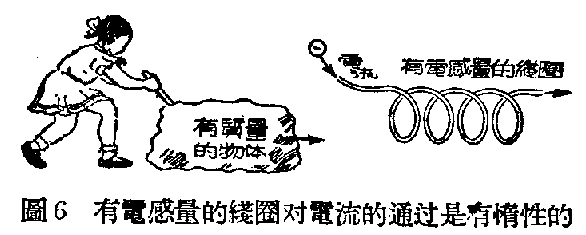
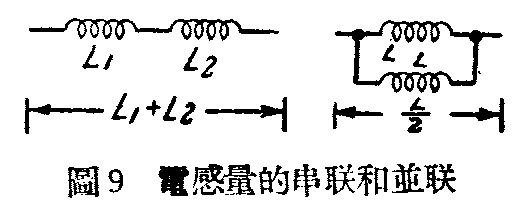
无线电里的线圈，就像任何东西的质量一样。一个东西，要它动，它不立刻动；已经动了，要它停又不能立刻停，就表示那东西有惰性，这是因为那东西有质量的缘故。物体的质量愈大，惰性也愈大，例如火车的惰性，大于汽车；电子是物质里质量最小的东西，所以它的惰性最小，我们一般认为电子是几乎没有惰性的（但到了电流变化极快的超短波频段，电子的惰性还必须考虑）。同样道理，线圈的圈数愈多，电感量愈大，它的惰性也愈大。如果两个线圈串联，电流通过时要遭遇到两个线圈的拒抗，所以电感量更大（等于每个线圈电感量的和）；但若将两个线圈并联，电流不能通过其中一个，还可以通过另一个，电流有另一条路可走，所以电感量反小了（如两线圈完全相同，电感量减半）。

线圈的惰性，除了与圈数有直接关系外，还与一定数量电流的增加所能增加的磁力线数有关。如果很小的电流增加就有增加很多磁力线的趋势，那么这电流的增加过程愈困难，也就是线圈的惰性愈大。换句话说，线圈的电感量L除了与圈数N成正比外，还有单位电流所能产生的磁力线Ф成正比。即

上式用M．K．C．单位制时，Ф的单位是韦伯，电流I的单位是安，L的单位是“亨”，在实用上这一个单位太小，常用的是毫亨（千分之一亨）和微亨（兆分之一亨）。

一个线圈，当通过电流I安时，所产生的磁力线是相当分散的。计算它们的数量Ф，有相当困难。因此实际求线圈的电感量多用经验公式。线圈的种类很多，有密绕的，一圈挨着一圈；有间绕的，一圈和一圈之间隔开了相当间隙；有铁心子的、铁粉心子和空心的；有单层的和多层的；多层的绕法还有很多花样。普通高频用的多是单层密绕的空心筒形线圈。求这种线圈的电感量，可用下列公式：

上式R及l为线圈半径和长度，单位都是公分，N为线圈的圈数，K为一与线圈的长度对直径的比值有关的因素，它的数值，列于下表：

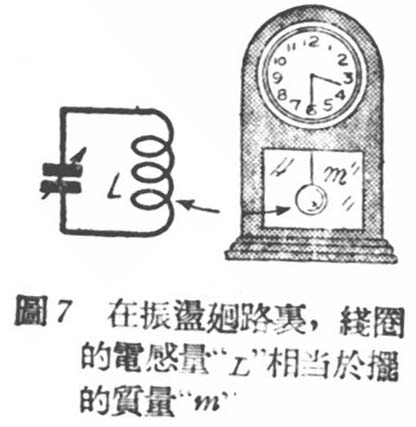
直径对长度比小于\(\frac{1}{10}\)的线圈，K的值都可假定为1。例如一线圈共60圈，直径和长度均为3.56公分，查表得K=0.6884，代入上式即求得

反过来，知道了所需要的电感量L和直径对长度的比值，也可以求圈数N和用多粗的线来绕制。设所需为200微亨，2Rl=0.4，K=0.8499,l=8.9公分，R=1.78公分。由上式得：

要在8.9公分的长度，密绕129圈，所以线的直径不得大于8.9129=0.069公分。

绕在铁心上的线圈，同样电流变化所产生的Ф的变化，比起空心线圈来可能要大得多。所以同样圈数的铁心线圈电感量，比空心线圈也可能大得多。但当铁心达到磁饱和状态时，电流的变动不影响磁力线的增减，这时电感量也可能为零，对电流的变动基本上失去了抗拒作用。所以铁心线圈的电感量容易做成为可变的，而空心线圈是不可变的。普通用铁粉心子的线圈和电容器做成的调谐回路，还可以改变铁粉心伸入线圈的多少改变电感量来调谐；而调谐回路若用空心线圈，就只好改变电容器的电容量来产生调谐。

线圈的电感量L愈大，也就是惰性愈大，对通过电流的抗拒愈大；这电流的频率f愈高，也就是电流变动得愈快，线圈表现反对它变动的能力也应当愈强，所以线圈的电抗作用应当和L及f成正比。计算这电抗X\(_{L}\)—又叫做“感抗”——的公式是：

式中L的单位是亨，f是每秒周数，X\(_{L}\)是感抗欧数。

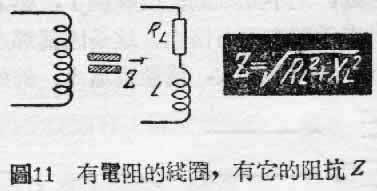
我们晓得，用导线绕成的线圈，难免要有电阻，而线圈有了电感量，它又有电抗。电阻和电抗都是反对电流通过线圈的，总起来说，就是线圈对电流有“阻抗”。一个线圈的阻抗，我们通常用Z\(_{L}\)来代表，ZL的计算公式是：

X\(_{L}\)的作用，只影响通过电流的大小，而R的作用还使电流通过线圈就发热，产生电能的消耗。所以一个线圈的质量如何，应当决定于XL对R的比值Q。为了要得到X\(_{L}\)我们不能避免有R，得到同样的XL而R最小，结果自然最理想。所以Q愈大的线圈愈好。普通收音机里高频和中频线圈的Q，一般为75到150。发信机里的线圈可能高到800—900左右。

由上面式（2），我们看出L和N\(^{2}\)成正比，因此X\(_{L}\)也和N2成正比，\(\frac{R}{l}\)小的线圈，要保持L不变，只好增加N。圈数增多，线也增长，为了不减小Q就非用较粗的导线绕制不可（因为线粗了电阻小，线长了电阻大）。有一种编织线，电阻很小，也常被采用来绕制高频线圈。这已经可以说明要做成一个好线圈，要R、l和导线都同时选择得当，并不是很容易的事。只有多做几只电感量相同的线圈，比较测试，方可得到最好的结果。（沈肇熙）