电子是带电荷的质点,虽然它的电荷量很小,但质量却也非常小,1098万亿亿亿颗电子才重一公斤,电荷量比质量的数值大1759亿倍,因为电子在电场里受电力的作用而运动的难易,主要由它的电荷量而决定,所以它就像没有任何质量,没有一点惰性一样很容易运动。它走一段空间距离,就像不要花时间一样。物理学告诉我们:当有一个力F加到质量为m的物体上时,就会产生加速度a,过一段时间t后,物体走出的距离为S。这些数量之间的关系是:
F=ma, a=\(\frac{F}{m}\)………………(1)
S=\(\frac{1}{2}\)at\(^{2}\),t=\(\sqrt{2s;a}\)…………(2)
在式(1)里,如果m小到几乎近于0,a就变成无穷大了;在式(2)里,如果a是无穷大,t应当是零。这就表示在电子质量假定近于零的条件下,走一段有限长的距离,就可以看成几乎不需要任何时间。

例如在阴极射线管里,电子由偏向屏到萤光幕,在偏向屏间电子受电力的作用,立刻表现为萤光幕上电子轨迹的运动;在收音机的放大电子管里,电子由阴极到屏极。只要栅极上一有电压的变动,立刻就有屏流的相应变动。
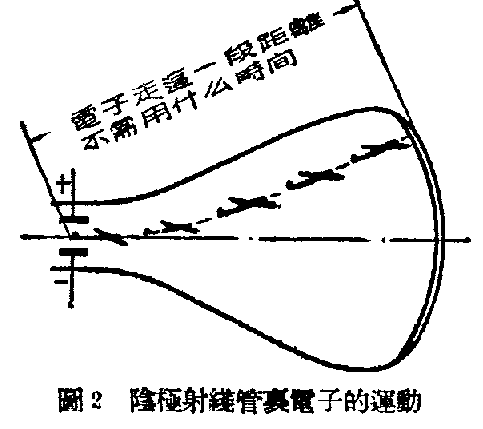
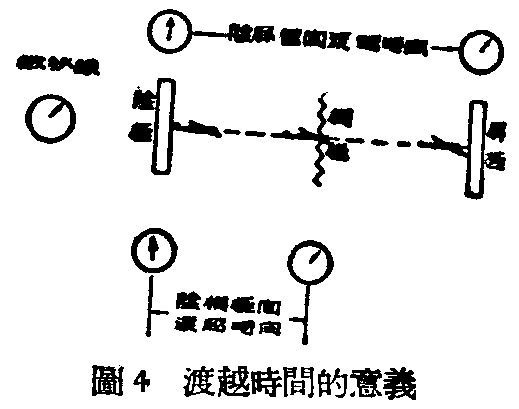
事实上,如上所述,电子还是有质量的,它的运动,也还要花一定的时间是肯定的。但由于在一般电子仪器和收音机的电子管里,它所走的距离很短,在管内极间飞渡的时间——叫做渡越时间,比起工作频率的一个周期来,要短得多,在实际影响上或人的感觉上,都可以忽略不计。例如一个电子管的屏阴极间距离为3公厘,屏极上加上比阴极电位高200伏的电压,渡越时间(由阴极到栅极)约为1万亿分之72秒,如果频率在30兆周以下,即周期在1百亿分之333秒以上,渡越时间就只占周期的0.21%,比较起来确实是微不足道的。
在超短波的领域里,当频率高到渡越时间和一周期的比值成为一个并不太小的分数时,这渡越时间就不能不计算了,所以电子在电子管内的渡越时间问题,是超短波带的重要问题。
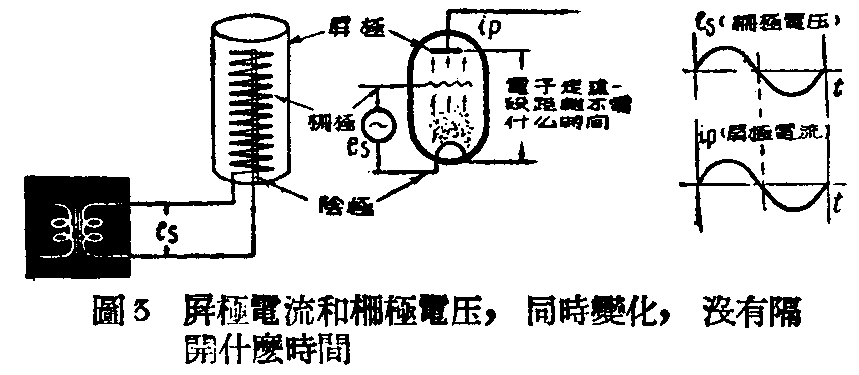
渡越时间对放大级的影响
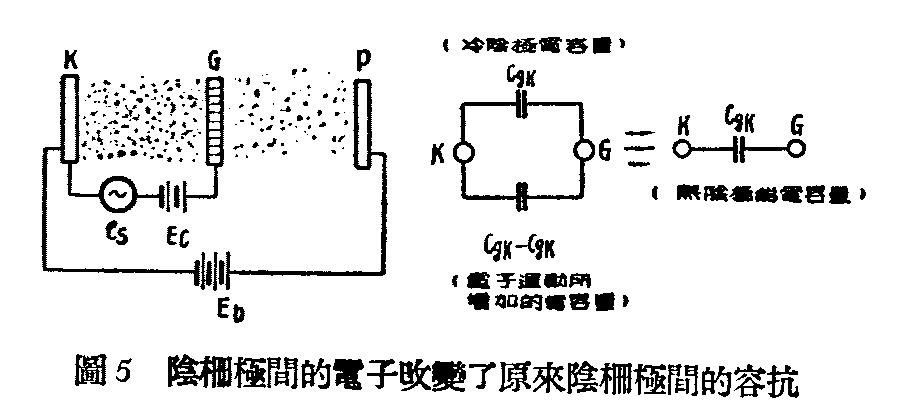
图5K板和P板分别表示三极管的阴极和屏极,G为栅极栅阴极间和栅屏极间的黑点代表电子在管内的分布。屏极上加正电压(对阴极来说)E\(_{b}\),栅极上除加负电压Ec外,还加有交流电压e\(_{s}\)。G、K组成一个电容器C'gk,在阴极没有发射电子以前,接上E\(_{c}\)时,就已经对这电容器充电,使得G上有电荷。阴极发射电子以后,电子在栅极上诱导出正电荷来,使得栅极上的电荷比原来充电的电荷不同,相当于C'gk有了改变,变成为C\(_{gk}\)。
现在因有e\(_{s}\)也加在栅极上,先假定es的频率很低,即e\(_{s}\)的变动很慢,在栅极附近电子数量的增加几和栅极电压的增加是同时的,因此栅极电流(等于电子数量的变化率)的相角在es前90度。所以对e\(_{s}\)来说,栅阴极的存在只不过像一个普通的电容器Cgk。
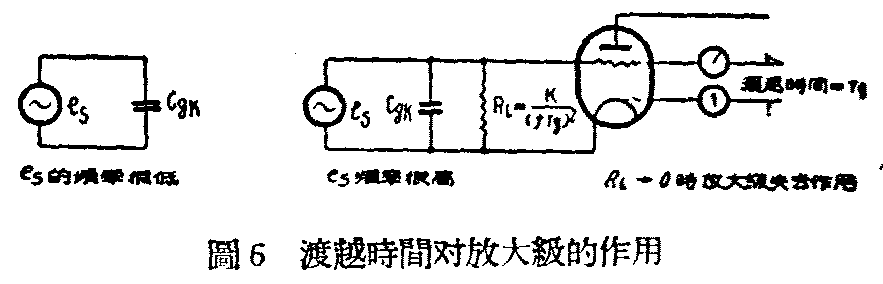
如e\(_{s}\)的频率很高,电子受es的作用,离开阴极的数量虽仍然是和e\(_{s}\)同相,但它们到达栅极附近所需要的时间Tg,就不能不计。因运行时间的存在,使栅极附近电荷量的变化,落后于e\(_{s}\)的变化一个相角θg。 例如e\(_{s}\)一周所占的时间为T,那末θg就等于360\(\frac{T}{_{g}}\)T。而在栅极感应出来的电流只超前es(90-θ\(_{g}\))度,而不是90度。对es来说,这时阴栅极已经不完全是一个电容量C\(_{gk}\),而是另外还像有一个电阻并联在电容量上一样。这个电阻,等于是es的负荷电阻R\(_{L}\)(图6),可以证明它和频率f和渡越时间Tg有关,它的计算式为:
R\(_{L}\)=K1(fTg)\(^{2}\)………………(3)
式(3)中K为比例常数。可见频率愈高,R\(_{L}\)愈小,到RL小到等于将e\(_{s}\)短路时,电子管便失去放大作用。所以渡越时间的影响在超短波带是相当严重的。
渡越时间对振荡级的影响
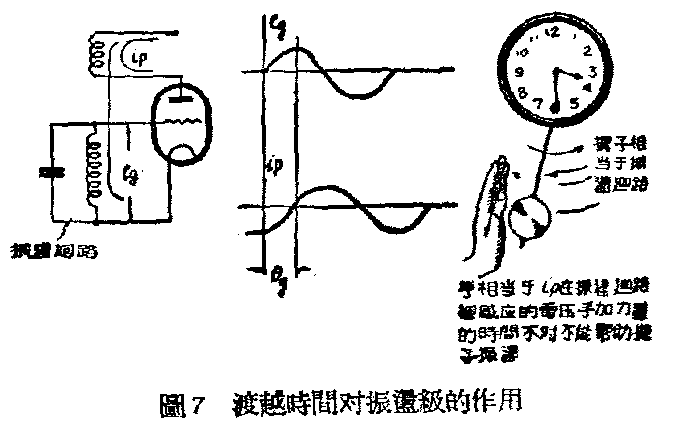
渡越时间除了影响电子管的放大性能外,对电子管帮助振荡回路振荡的能力也大有影响。因为电子管如果帮助振荡,屏极的输出回授到栅极,在栅极里产生的电压,一定要和栅极上原有的电压同相位。好像一个摆,用手来帮它来回摆动。如果手用力的方向和时间不对,就有可能反使摆停止下来。要得到这样的相位关系,屏流一定要和栅压相位相同,这只有当电子在阴极和屏极间的运行时间等于零时才能够做到。
一般分析电子管的问题,我们常想像屏流是屏压所产生,它们是同相位的。栅极上加一个电压e\(_{s}\),我们也当成是屏极上加一个同相的电压μes来看待,而放大系数μ为一常数。现在考虑渡越时间在内,屏流和e\(_{s}\)不同相,那末μ就不再是一个普通的常数,而应当是一个复数,即μ=μr-jμ\(_{i}\)。μr是μ的实数部分,μ\(_{i}\)是μ的虚数部分。
同样,电子管的其他常数如跨导G\(_{m}\)和内阻rp,在超短波带也变为复数。
由于电子管的常数变为复数,即使屏路负荷为一纯电阻,屏流感应到栅路内的电压也不可能和栅压同相,这样维持振荡回路振荡是有困难的,所以渡越时间也妨碍了电子管的振荡作用。
到了超短波频带,无线电回路里的特殊问题是很多的,本文所谈只是其中之一。(张启人)