任何一个晶体二极管里都有一块半导体的晶体,和两个金属电极。对于加在两电极上的交流电压会像普通二极管一样,产生整流作用。本文就是谈这种作用的原理。
电极和半导体的接触,有两种方式如图1:第一种是点接触式,用一电极和半导体接触于一点,整流作用就发生在这一点附近,另一电极和半导体接触于一个面上,没有整流作用,只用来和外面回路相联接;第二种是面接触式,两电极和半导体的接触都是面的接触,半导体里一部分掺入了阳性杂质,另一部分掺入阴性杂质,因此一部分是空穴导电性的,另一部分是电子导电性的,整流作用就发生在这两部分的接界处,两个电极都是为了对外面回路相联接。这接界处的附近范围,我们叫做“电子——空穴阻挡层”。
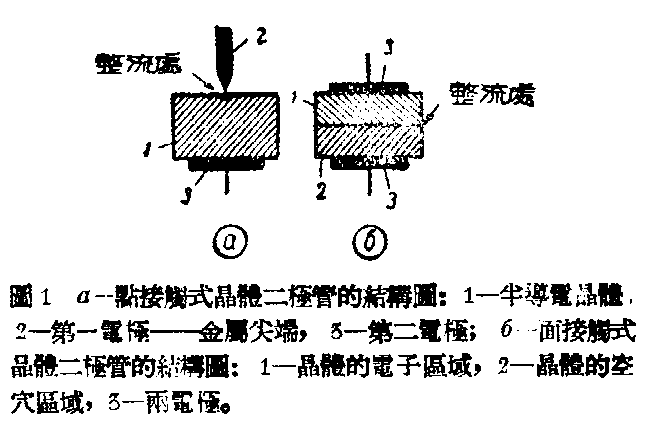
这两种接触方式整流作用的物理过程,本质上是相同的。我们下面专谈第二种方式整流作用的物理过程。
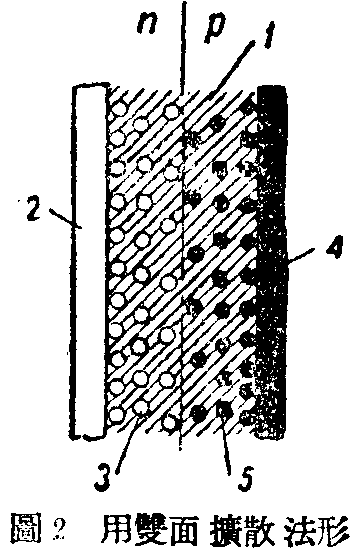
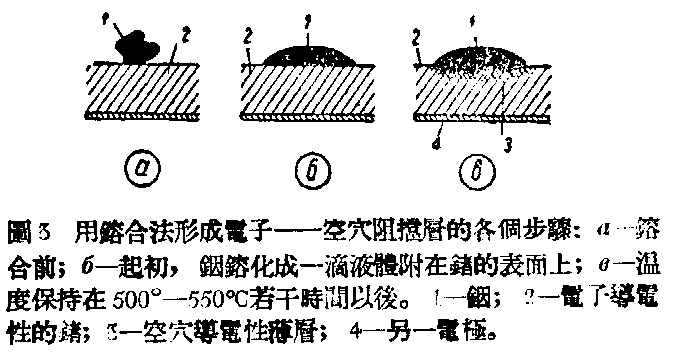
把阳性和阴性杂质掺入半导体的方法,常用的是双面扩散法如图2。制造锗二极管时,也用另外一种简单的方法来形成“电子——空穴阻挡层”。就是先制成一片具有电子导电性的锗晶体,把一小粒的铟放在锗片的一个表面上,加热到足够的高温(500—550℃)时,铟粒即熔化成一滴液体,附在锗的表面上并扩散到一定深度中去如图3。铟的熔点是156℃,锗的熔点是958℃,所以锗并不熔化。冷却以后,在铟滴附近的晶体片,有一层就有了很高的空穴导电性,和原来电子导电性的的锗晶体间就有了“电子——空穴阻挡层”。铟就成为这个空穴导电部分的接触电极,另一电极可用铅或锡焊在锗片的下面,这样可以获得可靠的电接触,但接触面上并没有整流作用。
“电子——空穴阻挡层”中位垒的发生
在“电子——空穴阻挡层”里自然形成的电位差,是这里能产生整流作用的直接原因。我们先用图4来分析一下这种接触电位形成的原因。图4α有含有杂质的两种导电性质不同的晶体,图4б和в是两种杂质在晶体内的浓度分布图。左边的一部分具有电子导电性,左边的一部分具有空穴导电性。为了简单起见,我们假定每一部分中杂质的分布都是均匀的。图中 和 分别是在热平衡条件下(即无外电压时)整个晶体内空穴浓度和电了浓度的分布图。
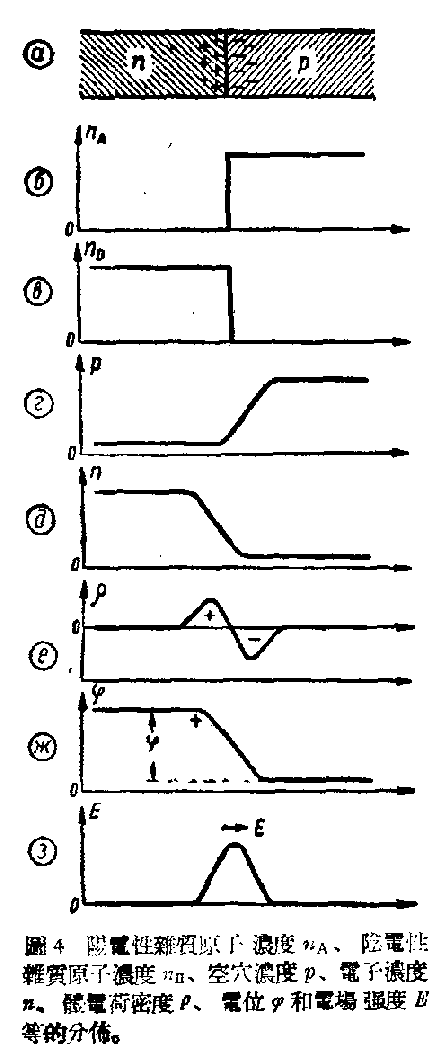
让我们看平衡形成的过程。由于电子浓度在电子区域内比在空穴区域内大,于是,电子就力图转移(扩散)到空穴区域内去。电荷随着一同转移。如是,空穴区域就被负电荷充电,而电子区域则带正电。同时,有电场发生,其方向是阻止电子转移的,也就是说,这电场使电子区域的电位较空穴区域的电位为正。由于电子扩散的结果,交界处的电场一直增大到使由电子区域转移到空穴区域去的“电子流”最后等于零为止。这样在电子区域和空穴区域间形成的电位差称为接触电位差。
这种现象和电子管整流管屏极上没有接到外面回路而聚有负电荷的情况类似。我们知道,阴极和异极间即使不加电压,电子也能由炽热的阴极飞出。飞出的电子到达整流管的屏极上,结果,屏极被充电成负电位,而阴极则成正电位。在阴极和屏极间发生一电场,这电场阻止电子由阴极向阳极转移。最后,电场一直增大到使所有飞出的电子一律折回,而电子由阴极向屏极的自发转移也就终止了。
但是,在“电子——空穴阻挡层”中形成的平衡并不意味着电子停止运动。由于热运动的结果,通过分界转移到两方去的电子的数目将相等。同时,能从电子区城进入空穴区域的,只有那些具有足以胜过反向电场的能量的电子,即其能量足以胜过位垒的电子。
位垒的高度由两区域间接触电位差的大小决定。在相反方向,空穴区域内为数不多的任何自由电子都能转移到电子区城去。这样,在平衡状态下,扩散电流就为因受接触电场作用而发生的传导电流所抵消。
在平衡状态下的“电子——空穴阻挡层”,也可以用空气的大气层来比喻。在平衡条件下,空气没有垂直运动(垂直风),但实际上,这乃是自下而上的扩散气流和因地心吸力自上而下的气流互相抵消的结果。
同时,空气的密度随高度的增加而减小,即随着空气质点位能的增加而减小。同样地,在半导体中,电子的密度也随着电子位能的增加而减小。
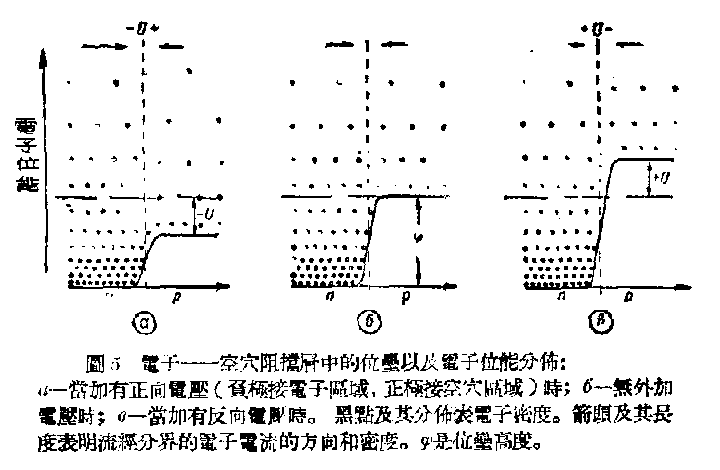
图5是平衡状态下空穴区域和电子区域内电子的密度和其位能的关系的图解。在没有外加电压时(图5,б),具有大于位垒高度的能量的电子在两区域内的密度相同。
以上对于电子来说的情况,也同样适用于空穴。空穴的浓度在空穴区域内比在电子区域内大,因之,在形成平衡的过程中,空穴力图转移到电子区域内去。因为空穴的电荷是正的,于是,由于空穴扩散而发生的电场的方向,就会和由于电子在相反方向转移而形成的电场的方向一致。在平衡状态下,空穴向一方的扩散电流为反方向的空穴的传导电流所平衡。
因形成平衡而发生的电荷,分布在“电子——空穴阻挡层”分界的附近,且在电子区域内为未被平衡的阴电性杂质原子的正电荷,在空穴区域内则为未被平衡的阳电性杂质原子的负电荷。
这种电荷的密度的分布和相应的电场强度的分布分别见图4的е和з。
这样,在分界附近的电子区域内就缺少电子,而在分界附近的空穴区域内也缺少空穴。因此,在靠近分界的区域上,“电荷负载者”的浓度降低,而电阻将增大。这个电阻增大的区域就是我们所说的阻挡层。
“电子——空穴阻挡层”整流作用的历程
现在,我们来研究,当两电极上有外加电压时,电流流经“电子——空穴阻挡层”的情况。
前已指出,当没有外加电压时,由电子区域流到空穴区域去的“电子流”为另一反向的“电子流”所平衡。同样,两方向的“空穴流”也平衡。
假定在“电子——空穴阻挡层”上加上若干外加电压,且使空穴区域和电源的负极相连,电子区域和正极相连。于是,阻挡层内的电场就增大,因之两区域内电子位能的相差也加大,即位垒高度增大。这时,电子区域内的电子和空穴区域内的空穴还要再减少,这就使得阻挡层的电阻也增加。
随着位垒高度的增加,电子区域内具有足以胜过位垒高度的能量的电子的数目就减少,即流入空穴区域内的电子流减小(图5,в)。当电压加至数千伏特时,从电子区域流入空穴区域的电子流将实际终止。而反向的“电子流”则实际仍旧不变。事实上,这时晶体内的电场使所有由空穴区域向电子区域运动的电子加速,因此,电流将主要取次于空穴区域内电子的密度和形成的速度,取决于电子与空穴重行结合的速度,而受外加电压的影响实际甚微。
“空穴流”经位垒也有类似的情况。加以上述极性的外加电压,对于空穴区域内的空穴的位垒也就增大。结果,从空穴区域到电子区域的“空穴流”就减小;同时,从电子区域到空穴区域的空穴则实际不变。因此,随着外加电压的增大,所得的净的“空穴流”就迅速趋于饱和,和“电子流”的情况一样。
因此,总的饱和电流是由“电子流”和 “空穴流”两部分组成的。前者由空穴区域流入电子区域,后者则相反。也就是说,总的饱和电流是由两区域内的非主要电荷负载者的浓度确定的。
在“电子——空穴阻挡层”上加以极性相反的电位差,位垒高度就减小,因此,从电子区域经阻挡层流入空穴区域的“电子流”就加大(图5,α)。同时,反向的“电子流”则保持不变。
因此,所得的净的电子电流的方向将是从电子区域到空穴区域,且这电流将随外加电压的增加而增加。对于空穴电流也存在有类似的情况。
应当指出,这种现象和电子的热放射有很多类似的地方。在电子的热放射中,只有那些具有足以胜过位垒的能量的电子才能从阴极飞出。位垒愈高,则电子飞出时所要作的功愈大,因此,在同样温度下,阴极发出的“电子流”就愈小。与此类似,在“电子——空穴阻挡层”中,主要电荷负载者形威的电流的数值是由位垒高度决定的,因此,也就由外加电压的数值决定。
因为净的“电子流”和净的“空穴流”是在相反的方向上,因此它们所形成的电流将在同一方向上,即总电流等于电子电流Iэ和空穴电流Iд的和。总电流和电压V的关系以下式表示:
I=I\(_{з}\)+Iд=I\(_{ο}\)(е\(^{-}\)αU-1)
式中I\(_{O}\)=Iзο+I\(_{дο}\); α=\(\frac{е}{KT}\),其中Iзο是饱和电子电流,I\(_{дο}\)是饱和空穴电流,е是电子所带的电荷值,K是波茨曼常数(1.38×10-23焦耳/每度),T是绝对温度。在室温下ο=40\(^{I}\)/伏。
据此公式,在足够大的正电压下,即,当е\(^{-}\)αU>1时,电流数值将按指数规律增加。在负电压时,е-αU减小,因此电流就迅速地趋于常数值I\(_{0}\)。“电子——空穴阻挡层”式晶体二极管的伏安特性曲线的形状如图6。
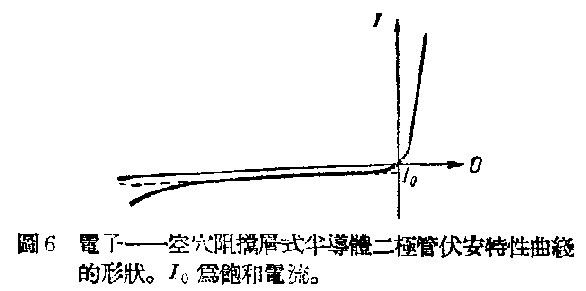
于是,流过晶体二极管的电流数值,就由外加电压的数值和符号决定。相当于低电阻的电流方向称为通流方向或正方向。相当于高电阻的相反方向则称为阻流方向或反方向。
对于“电子——空穴阻挡层”式晶体二极管,和电流的正方向相当的极性是:正极接空穴区域,负极接电子区域。
(苏联)H.别宁原著,原文载苏联无线电杂志1954年9月号,钟建安译。本刊编写。