数字世界中的美丽——编程实现千姿百态的树叶
编程爱好者
编者按:用程序绘制一些简单的图案,这样的内容我们以前也为读者作过介绍。但与以往不同的是你能想到用相对简单的算法就能实现如此多变、写实、美丽的图案吗?除了丰富的树叶图案之外,将程序的参数稍加改动,竟然能够实现浪花、宝塔等完全不相干的图案。想知道其中的秘密吗?细读本文就会让你大有收获。
心动就要行动
走到户外,欣赏大自然的美景,映入眼帘的是千姿百态的各种各样美丽的植物。这不禁使人在心旷神怡之余开始赞叹大自然的伟大。心动了吗?其实我们编程爱好者完全有能力将它们用电脑绘制出来,那就让我们行动吧。
经过一番探索,程序编出来了(程序下载地址:http://www.mydown.com/soft/209/209168.html),画出的图案还真不少,如图1所示,笔者根据其形状命名的有蕨叶、芦苇、叶脉、文竹、大树、嫩藤、小草、葡萄、迎客松、玫瑰花、五星花、蒲公英等图案。甚至随着参数的调整,我们还能通过程序得到塔、羽毛、浪花、稻草人等其他图案。


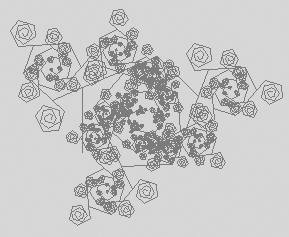
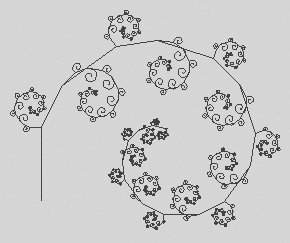


实现原理
既然通过一个简短的程序能得到如此丰富的结果,那我们一定要先来探究一下它的实现原理了。首先我们仔细观察这些图形有何规律,这种规律就是自相似性,一棵树分出的一个叉又是一棵小树。
为了说明原理,笔者以二维情况下非常典型的一棵小树为例来介绍画图的算法。
设这棵树发了两个叉,如图2深色部分所示。沿着箭头的方向,画这棵树需要如下步骤。
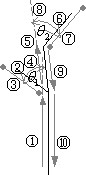
①首先从起点开始向前走到第一个分叉点,设距离是L1;
②向左转θ1 ;
③画子树;
④向右转回θ1 ,然后再向左转θ,这个θ角相当于树的曲度;
⑤继续向前走到第二个分叉点,又走了L2的距离;
⑥向右转θ2 ;
⑦画子树;
⑧向左转θ2,考虑到如果树枝下面还有枝节,应该再向左多转θ表示树的曲度;
⑨向右转回θ,后退L2,回到第二个分叉点;
⑩向右转回θ,后退L1,回到起点。
至此一棵完整的树就诞生了。
算法分析:在算法中,③、⑦用到了递归方法,对自身进行调用,正是这一步骤模拟了自然界树木的生长。⑨、⑩两个步骤为回溯算法,保证画完子树之后能退回到转弯时的出发点。
核心代码解析
下面我们就来看看要实现如此美丽效果的程序的核心代码:
Sub leaf(ByVal n As Integer, ByVal l As Single)
'蕨叶(n为递归深度,大小为L)和树结构类似
Dim i As Integer 'i是循环变量
If n = 0 Then Exit Sub '递归的结束条件
For i = branch To 1 Step -1 'branch枝条数
FD L1 * i / branch * l
LT Seta1
leaf n - 1, i / branch * l / K1 '左子树大小的比例系数为K1
RT Seta1 - Seta '树的曲度为Seta
FD L2 * i / branch * l
RT Seta2
leaf n - 1, i / branch * l / K2 '右子树大小的比例系数为K1
LT Seta2 + Seta
Next i
For i = 1 To branch '回溯主叶干
RT Seta
BK L2 * i / branch * l
RT Seta
BK L1 * i / branch * l
Next i
End Sub
程序说明:
本程序为多枝条树的画法,主要是用递归和循环来描述的。对于程序究竟是怎么执行的,聪明的你还需要动脑筋去想一想,这可是使你更加深刻理解递归和循环的好机会啊。
在程序中调用了一些称为海龟作图的函数,假设有一只听话的小海龟在受你的控制,它能听懂如下命令:FD n,在当前位置上前进n步;BK n,在当前位置上后退n步;RT n,在当前位置上向右转n度;LT n,在当前位置上向左转n度。这些函数用VB的Line语句能很好实现,这里就不再详细介绍了。
代码可能比较枯燥,但看着那些美丽的效果你就会感受到编程的无穷乐趣了。

程序拓展与小结
在程序运行时可以方便地调节各个参数,通过调整比例系数可以改变子树的大小,从而决定画出的形状更像树枝还是更像树叶;调整子树的倾斜角度可以形成不同的树种;在各个参数中曲度对树的形状影响最大,调整它可以生成不同类别的图案。使用动画按钮还可观察到一个树叶从小到大的生长过程。
通过编程画出了这些千姿百态的树形图案,这些图案也许从几何层面上揭示了自然界的生物生长、海浪等现象的原理,那就是整体是由自身的部分不断复制而形成的。
对程序的拓展:
①如果增加三维功能,则可描绘出更加逼真的树叶。
②只要稍微变换一下绘制规则,还可画出各种类似的具有分形规律的图形。
赶快动手吧,大自然蕴含的无穷规律正等待我们去不断探索,不断发现。本文所提到的程序下载地址为:http://www.mydown.com/soft/209/209168.html