解答“八皇后问题”
软件世界
前言:“八皇后问题”是计算机科学中的一个著名的问题,它的典型解法充分体现了递归的特性。此外,非递归及回溯等也可以有效地解决这个问题。对“八皇后问题”的解法熟悉之后,对相应的迷宫求解等问题也就有了基础了。在面对更多的“N皇后”求解的时候,由于受限于堆栈的容量,递归深度将受限,我们在求解的时候还能学习到更多的东西。
提出问题
“八皇后”中的“皇后”,指的是国际象棋中的皇后。在国际象棋中皇后能把同在一行、列和两条对角线上的棋子吃掉,如果在8×8的国际象棋棋盘中放8个皇后,并且不能互相吃掉,有多少种放法呢?这就是我们要解答的“八皇后问题”。
在解决一些复杂问题时,很多情况下我们都是不直接入手,而是先间接分析与它相近的、相对要简单一点的问题。像八皇后问题就可以先分析四皇后,也就是“把4个皇后放在4×4的国际象棋棋盘里,并且不能互相吃掉,有多少种放法?”下面我们就来看看分析的思路。
理清思路
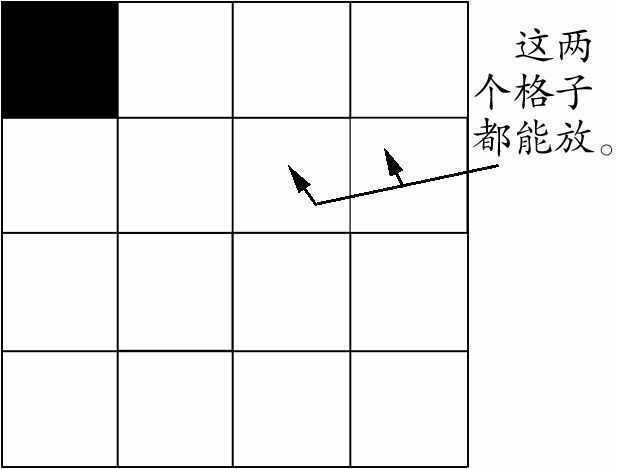
在纸上画好4×4的格子做棋盘,再准备4个棋子。都做好了就把第一个棋子放在第一行第一列的格子里(如图1)。根据问题的要求好好看看,我们可以尝试放下第二个棋子(如图2)。当要放下第三个棋子时,突然发现没有地方了,这就说明前面的放法是不正确的。那么是前面的两个都没放对,还是只有某一个呢?我们来分析一下。
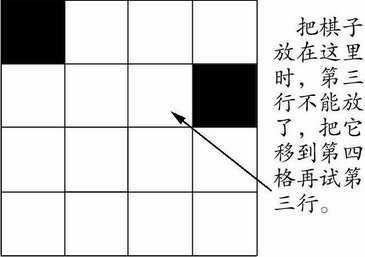
第三行全部不能放是由哪些棋子决定的?如图三,可以看出第三个棋子没法放是由前面两个棋子共同作用造成的。如图四,第二个放的棋子的位置是不唯一的,既然前面的放法不对,我们可以尝试改变第二个棋子的放法。这里给我们了启示,要对每一行的所有可能放的格子都尝试一遍。
总结规律
分析完了就依着前面的分析继续下去。第三个棋子没地方放,可以理解为是按第一个和第二个棋子的放法已经没有了解法。那么就回到最近的第二个,如图五,把以前的棋子移到它的下一个可放的位置,再试第三行,如图六,现在第三行第二格能放了。接下来按前面的方法试第四行,怎么又是没有一个格子能放,现在我们有了解决它的办法,就是回到上一行把以前的棋子往新的可以放的位置放。
我们看图六,第三行的后面两个位置也不能放了,那就再往上推,第二行的棋子已经是最后一格了,接着往上推,现在回到了第一行,同样是把以前的第一格移到第二格,再试下去。如果第四行能放棋子呢?你就祝贺自己吧,找到了一个解。怎么才算是全部试完?根据前面的分析知道,第一行在最上面,它放棋子的位置决定了下面所有行棋子的放法,它没地方放了,下面的行也就不用放了。
现在总结规律如下:
1.需要从第一行第一列开始,尝试每一行的所有可能;
2.当放一个棋子时,需要检查同一行、列和两条对角线上是否已经存在棋子;
3.当某一行不能再放时就回到上一行,把以前的棋子放到下一个可放的格子上,如果也不能放了就再往回推;
4.如果一直放到最后一行也能放棋子,那就找到了一个解;
5.第一行的所有格子开头的都放完了就全部试完了。
具体的代码和详细的解释可以在http://www.cpcw.com/40/code.rar下载,八皇后有92个解,四皇后有2个解。