描绘更真实的世界——ATi 3Dc纹理压缩技术解析
硬件周刊
ATi和NVIDIA每次发布新显卡,总会有新的图形技术闪亮登场。这次随着R420的发布,3Dc纹理压缩技术终于走向了前台。
什么是纹理贴图
提到纹理压缩,我们仍要从最初的纹理贴图说起。从3D游戏诞生起,纹理贴图就作为描绘游戏世界最重要的手段之一发展起来。在3D游戏中,大部分物体都是以3D模型加纹理贴图来构成的。简单来说,游戏中的一栋建筑,我们首先要使用3D建模将其模型构建出来,而表现模型外观的材质、颜色等等都需要将纹理图片贴在模型上,这样就完成了游戏中建筑的构建。不仅建筑这种简单模型,就是游戏中的千变万化的人脸,也是采用脸部模型加脸部各部位贴图来制作的。恰当地使用贴图,可以在使用较少的多边型的前提下,逼真地描绘出各种物体。
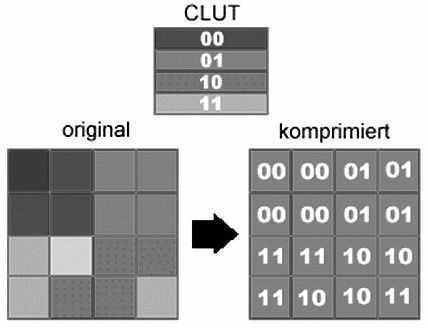
DXTC压缩原理示意图
随着3D游戏的发展,人们对纹理贴图的要求也越来越高。首先是对纹理的分辨率要求越来越高,纹理贴图一般是以正方形存在的,其分辨率已经从最初的32×32、256×256发展到今天的4096×4096甚至更高。纹理的分辨率越高,物体看起来越真实,当然其数据量就越大。在游戏运行时,显卡必然是在同屏创建若干物体模型,也必然要向显存里调用相当数量的不同贴图,此时高分辨率的纹理就对显存的容量和显卡的传输带宽、传输速度提出了极高的要求,往往使显卡不能承受之重。
纹理压缩的出现
在这种情况下,纹理压缩技术出现了。它可以将纹理压缩成显示芯片可以识别的一种格式,然后将压缩后的数据存储进显存,最后再用显示芯片把压缩数据进行解压缩,经过运算后贴图到3D模型上。曾经出现过3种主要的压缩方法:PowerVR的Vector QuantizATion矢量压缩(VQ);S3的S3TC,后来微软将S3TC集成在DirectX 6中,并改称DXTC,在微软的支持下,DXTC逐渐成为业界的标准,并沿用至今;当年的3dfx也推出了一种纹理压缩技术FXT1,可以看做是DXTC的改进版,最大压缩率可以达到8:1,可以工作在Windows、MacOS、Linux和BeOS下。但由于DXTC已成气候,再加上3dfx被收购,FXT1也就无疾而终。
这三种压缩方法都是将纹理划分为一个个图素单元,然后根据颜色的不同,建立索引表,再用索引表中的地址(索引号)来代替原数据,这样数据量将大幅度减少。不同的是VQ只为整个纹理建立一个索引表,纹理越大压缩率越高,而DXTC和FXT1在纹理的多个部分建立不同的索引表,因此对小纹理的压缩效果同大纹理的一样好。
贴图技术的发展变化
①凹凸贴图
随着图形技术的发展,更先进的贴图技术出现了。其中一个很重要的就是凹凸贴图,它是一种在3D场景中模拟粗糙表面的技术。像自然界中树木的表皮、破旧的墙体……如果我们想依靠3D建模将它们制作出来,非常麻烦,凹凸贴图就可以轻松解决这个问题。比如说我们要实现一个粗糙凹凸墙面效果,首先将墙面的深度变化保存到一张贴图中,这个深度变化贴图看起来有点类似于我们在PHOTOSHOP中得到的灰色的浮雕效果图。然后再将深度变化贴图和原有的砖墙贴图在3D模型表面进行标准的混合贴图处理,即可得到具有凹凸感的表面效果。当然这只是凹凸贴图最简单的处理方法,其他方法会在这个基础上进行更复杂的运算。
②法线贴图
在凹凸贴图的基础上慢慢又发展出来了Normal Map(法线贴图)技术。法线贴图就是记录了一个需要进行光影变换的贴图上的各个点的凹凸情况的贴图,显示芯片根据这个贴图的内容,来实时地生成有光影变换的贴图,从而实现立体效果。法线这个概念我们在初中物理中都接触过,它是通过入射点垂直于反射面的直线。只要确定了3D模型每个顶点的法线位置和光源位置,我们就能精确计算出光在外表面所造成的反射效果。这种高低不平的反射效果如果用美术中的素描来表现的话,必然是有些地方描绘的颜色深些,有些地方画得淡些、浅些。这就是所谓的“用光与影描绘物体的体积”。所以只要我们记录了每个点的法线位置,就可以在后期计算生成逼真的凹凸3D效果。
那法线贴图具体是如何生成的呢?首先这里的法线要放到一个三维空间来考虑,只有这样才能确定立体空间中光线的方向。所以这里的法线是一个具有X轴、Y轴、Z轴三个分量的三维向量。我们可以用红、绿、蓝(即R、G、B)三种颜色分别来对应X轴、Y轴、Z轴三个分量,并用红、绿、蓝三种颜色的深浅来对应X轴、Y轴、Z轴三个分量的值。这样一张正常贴图就可以生成一张对应的由红、绿、蓝三色构成的法线贴图。大家应该注意的是,法线贴图虽然名为贴图,但它并没有真正贴在3D模型表面,只是为最终的光线、阴影计算提供了依据,这也是它和普通贴图不一样的地方。而且,真正的法线贴图记录的并不是贴图上每个点的法线的绝对角度,而是记录其相对于平面的一个差值。这样的话,随着视角的变换也能够实现即时的法线运算。
③法线贴图的优势
利用凹凸贴图技术制作的地球模型,很有立体感
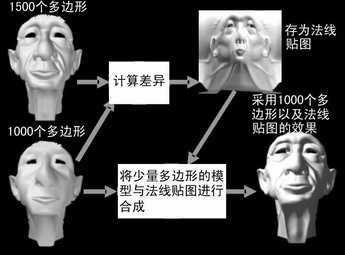
法线贴图的意义不仅在于实时生成新的有光影变换的贴图,更重要的是在游戏制作中,法线贴图提供了一个“取巧”的办法,可以使用较少的多边形运算来尽可能逼真地表现物体细部。比如,对一个游戏中的人物角色,可以为它建两个模型,一个使用了大量的多边形,用尽可能多的多边形来捕捉它所有的细微表现。另一个仅使用少量多边形,只要有足够能力来捕捉人物的整体形状即可。然后我们以第一个使用大量的多边形的人物模型为基础,建立法线贴图。而在实际游戏中,我们使用的是第二个少量多边形的模型,只不过我们在其表面使用了大量多边形的模型生成的法线贴图,这样就达到了以尽可能小的代价,描绘尽可能多的细节的目的。有时候为了进一步刻画模型局部细节,还要在模型某些重要局部使用分辨率极高的普通贴图,最终一个逼真的游戏人物就诞生了。如今这种方法已经被大量利用到顶尖的3D游戏中来,比如Half-life2、Doom3、Far Cry等都利用了它。
法线贴图加双模型,可以使用较少的多边形运算,来逼真地表现物体细部
3Dc纹理压缩技术
①3Dc技术的出现
但是同时使用普通贴图和法线贴图,就是在最理想状况下,它对显存和带宽的要求也将是仅使用普通贴图的两倍。显示系统的压力随着法线贴图的大量使用,越来越大。而且随着时间的推移、技术的进步,普通贴图也不仅仅局限于附带色彩这一种信息了,光泽度、粗糙、透明度等信息都已或多或少地包含在纹理中了。而这无疑又加大了纹理的体积和对显存和带宽的压力。
在这种情况下,我们自然会考虑到前面介绍过的DXTC纹理压缩技术。但DXTC纹理压缩技术出现于DirectX 6时代,它对付普通的色彩贴图是绰绰有余,但对于在其后才出现的法线贴图和多样性的纹理,DXTC就难以应付,不但效率低,而且失真也比较严重。对于法线贴图来讲,过量的失真是很难以接受的,普通贴图的失真无非是一些点的颜色没有和纹理保持一致,这在游戏中是很难发现的。但对于法线贴图来讲,它的每个点的颜色反映的是该点法线的角度,也就是该点的凹凸的信息,如果这些信息丢失了,带来的结果就会严重得多──一个阴影区域忽然出现了一个不该有的亮斑,这是一个多么糟糕的事情。所以在没有有效的解决法线贴图的压缩之前,很多游戏开发人员都在控制法线贴图的使用,甚至在某些时候为了降低系统要求和避免过度的失真,干脆舍弃了法线贴图的使用。
现在随着R420的发布,ATi提出了一个新的纹理压缩技术──3Dc纹理压缩技术。它的主要用途有两大方面:首先是可以以4∶1的比例压缩法线贴图,其次是可以把多样性的纹理封装成单一的材质。正好有效地解决了上述的两个难题。
②3Dc技术的原理
3Dc压缩技术是一种基于区块的压缩方式。在压缩的过程中首先将要压缩的法线贴图进行分块,再对每一个单独的区块进行压缩。ATi选择的区块大小是4×4,所以每个区块包含了16个点。我们前面讲过,法线贴图是用红、绿、蓝3种颜色的深浅对应X、Y、Z 3个轴的值,来记录每个点法线的方向,所以每个区块的这16个点也就可以对应地量化为X、Y、Z,3个4×4的矩阵,每个矩阵有16个值。
由于法线这个向量是一个仅仅表示方向的,所以我们可以将向量的长度都取“1”,然后利用公式X2+Y2+Z2=12,将Z值在后期算出,所以在实际工作中我们只需要压缩X、Y两个分量就可以了。X、Y两个分量的压缩方法是完全一致的,这里我们以X分量为例说明。
现在我们已经有一个关于X分量的由16个数组成的矩阵。首先提取这16个数中的最大值和最小值,然后在这最大值和最小值之间等分7份,最后将得出的中间的6个值插进刚刚统计得来的最大值和最小值之间。我们举个简单的例子,假设一个X分量4×4的矩阵,其中最大值是236,最小值是124。它们的差是112,将这112分成7份,每份就是16。所以可以算出这8个数分别为:124、140、156、172、188、204、220、236,这其中除了最小值、最大值,剩下的6个数都是计算得来的(在法线贴图的单通道颜色表示中,实际上采用的是8bit二进制数,这里为了说明方便,我们转化为了十进制)。所以我们在记录这个关于X分量的矩阵时就能够舍弃原来的16个数,转而使用两个数(最大值和最小值)就能表示了,两个数自然要比16个数占的空间要小,这就是压缩。
除此外,我们还要设定那些不是最大值也不是最小值的点究竟应该如何取值。这次采用的是序号记录法。我们仍然举例说明,首先我们要将这8个插值数从0到7编上序号,然后我们以这个矩阵中的一个大小为200的数值为例,它既不是最大值,也不是最小值,而且也不和计算出的8个数值重合,所以必然要被插值代替,经过比较使用插值中最近似的204来代替它,204的序号是5,我们只要记录这个序号即可,而8个序号只不过占用了3bit的二进制空间,这样也起到了压缩作用。
③3Dc技术的效果
所以我们的最终压缩结果是:区块中的每个点需要分别用3bit记录X分量和Y分量的数值的编号,然后再分别开辟两个8bit空间记录这16个点中的两个分量的最大值以及最小值,这样总共需要的空间就是(16×3+8×2)×2=128bit。而原始图像采用的是32bit的标准位图来存储的信息,R、G、B 3个色彩通道的深浅(即颜色值)分别表示X、Y、Z轴的分量值,还有一个用来记录Alpha信息的通道被浪费了,这样16个点每个点都需要4个8bit的空间来记录相应的信息,总的占用空间就是4×8×16=512bit。所以3Dc的最终压缩比是4:1,相当不错。即使原始信息是16bit,最终压缩比也可以达到2:1,不过从这点也可以看出,色深越高3Dc的作用越大。
三中法线贴图效果对比
而且3Dc可以在保证4:1的压缩率的前提下,尽可能地控制失真。前文讲过,我们在压缩取值时,都取的是近似值,这必然会带来失真,但每个数值失真的幅度最大不会超过16。而且随着区块的最大、最小值的变化,失真幅度也会随之变化,由于在实际游戏中一个4×4的区块中两个极值的差通常会比较接近,所以实际印中3Dc的失真的影响也会比较小。
3Dc纹理压缩技术压缩比高、失真小,可以让开发人员使用更高的分辨率和更为细致的法线贴图来制作更为逼真的游戏。如果换个角度,我们也可以使用一般精度的法线贴图,同时使用3Dc纹理压缩,这样必然会降低法线贴图对显存和带宽的要求,从而提高游戏速度。此外,对开发人员来讲,3Dc的使用也十分简单,DXTC所使用的压缩工具只要稍做调整就可以适用于3Dc,在压缩法线贴图方面3Dc也只多了两道指令,这非常有利于3Dc纹理压缩技术的普及。