股票收益早知道
软件世界
编者按
第4期E12版我们介绍了怎样用Excel 2002/2003在家建“大户室”,得到了广大股民的欢迎。这期小编特组织了用Excel计算股票收益的文章,希望读者朋友们喜欢(文中涉及的股票代码和名称等数据纯属虚构)。
为了规避风险,股民往往同时持有几只股票。由于股票收益的计算方法比较复杂,很难像银行存款利息那样处理。如果利用Excel进行股票收益管理,不仅可以做到盈亏一目了然,还可以帮助你确定每一只股票的保本卖出价。
一、计算股票收益
股票收益不仅受价格的影响,而且交易时还要缴纳各种税费。
1.建立交易工作表
新建一个Excel工作表,按图1样式在第1行各单元格输入列标记(字段),从第二行开始依次输入股票的各项数据,例如代码、股票名称、买入日期、买入价和买入数量等。以后每买入一次股票,按图1中的数据格式顺序增加一条记录即可。
2.计算股票买入总价
由于买入股票不仅需要支付股票价款,还需要支付股票交易印花税和交易佣金。所以股票买入总价的计算公式是“买入金额=买入价×买入数量+股票交易印花税+交易佣金”。为了适应股票交易印花税和交易佣金(手续费)的变化,可以在M1、N1单元格分别输入“股票交易印花税”和“交易佣金”字样,然后在其下方的M2、N2单元格中输入当前税率0.002(即2‰)和佣金标准0.002(即2‰)。再选中存放买入金额计算公式的G2单元格,输入公式“=E2*F2+(E2*F2)*$M$2+(E2*F2)*$N$2”,回车后就可以得到本次股票买入需要支付的总金额。
公式设计完成后,只要在E2和F2单元格中输入股票的买入价和买入数量,就可以在G2单元格看到本次买入交易需要支付的总金额(含印花税和交易佣金)。
将此公式复制到G3、G4等单元格,就可以得到买入其他股票需要支付的总金额。
提示:公式中E2、F2、G2等单元格由图1所示的表结构确定,朋友们可以根据自己建立的表结构确定公式。
3.计算股票可变现金额
卖出股票与买入股票一样,都要支付印花税和交易佣金,这两部分价款需要从卖出金额中扣除。所以卖出股票后实际获得的资金是这样计算的:“卖出金额=卖出价×卖出数量-股票交易印花税-交易佣金”。选中K2单元格,输入公式“=I2*J2-(I2*J2)*$M$2-(I2*J2)*$N$2”,就可以得到本次股票卖出获得的可变现金额(已经支付了股票交易印花税和交易佣金)。
当朋友们要将上次买入的股票卖出时,只须在I2、I3等单元格中输入卖出价,在J2、J3等单元格中输入卖出数量,公式就可以自动计算出卖出股票获得的可变现金额。
4.计算股票盈亏
股票交易盈亏的计算公式比较简单,用卖出金额减去买入金额就可以得到盈亏结果。在L2单元格中输入公式“=K2-G2”,回车即可获得本次交易的盈亏结果。
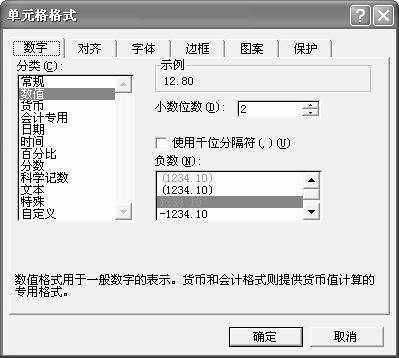
提示:为了使交易盈亏更明显,可以选中L2、L3等单元格,单击“格式→单元格”命令,进入“数字”选项卡;选中“分类”栏中的“数值”,然后选中“负数”栏中的红色负数格式;最后单击“确定”按钮。以后只要计算出的交易结果是亏损的,则结果都会用醒目的红色数字显示。
二、确定卖出底价
由于股票买卖均须支付交易印花税和交易佣金,并不是卖出价高于买入价就可以获利,所以股民有必要知道支付交易成本之后,买卖收支相抵时的卖出底价是多少。下面介绍用Excel的单变量求解工具解决这个问题的过程。
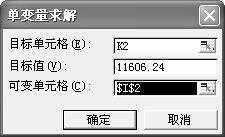
1.设定求解目标
对图1所示的股票交易工作表而言,我们的目标是确定支付了交易成本之后,“卖出金额”与“买入金额”相等时的“卖出价”应该是多少。以代码为000666的股票为例,K2就是目标单元格。选中K2单元格,单击“工具→单变量求解”命令,打开“单变量求解”对话框(图3),这时“目标单元格”框内显示为“K2”。根据上面确定的求解目标,“卖出金额”与“买入金额”至少要相等,所以“目标值”至少为11606.24。
提示:若要实现交易盈利,则“目标值”应该填入一个大于11606.24的值,预期的盈利越多,“目标值”就设得越大。
单击“可变单元格”框,然后选中图1中的I2使“$I$2”进入框中。它就是我们要寻找的“卖出金额”与“买入金额”相等时的卖出底价。
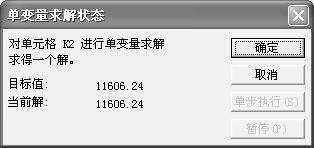
2.查看结果
如图3中的各项参数确定以后,单击“确定”按钮会弹出如图4所示的对话框,这说明单变量求解已经找到了符合约束条件的结果。这时图1中I2单元格中的数值就变成11.65285。也就是说支付了股票交易成本之后,000666号股票盈亏相抵的卖出底价应为11.65285,低于这个价格卖出股票肯定要亏本。
提示:如果不需要保存单变量求解的结果,那么,在看到I2单元格中的求解结果以后,只要单击图4中的“取消”按钮,就可以关闭对话框并将股票交易工作表中的数据复原。