趣味数学编程题解之牛顿的楼梯有多少种走法
IT商界
有时编程还需要点猜测和假想。
规律有时很简单,有时摆在了面前却混然不觉……
编程有时需要灵感,有时在找规律时需要有大胆猜测的勇气。下面的故事就是一例,你先自己猜测一下,看看能猜出它是什么。
题目:牛顿家的楼梯
牛顿家住在楼上,上楼自然要走楼梯。走的时间长了,牛顿忽然冒出一个想法,他家的18级楼梯对他来说有多少种走法呢?他一步可以走1级,也可以上2级,最多只能上3级。
级数和走法的关系
看的过程中,最重要的是看有没有什么规律可循。
级数 走法(总) 走法(分写)
1 1 1
2 2 2
3 4 4
4 7 4+2+1
5 13 7+4+2
……
从上面的分析中我们可以看出:
1、2、3级没什么规律,但4、5……就开始有规律了,后一级等于前面3个台阶走法的和,这正是它们的规律,也正是我们编程的依据。
方法一:循环法解牛顿的问题
正是因为有了上面的规律,我们可以以级数作为主线,一个一个地往下数,从1、2、3级一直到18级。OK,下面使用这种方法将它模拟出来,模拟过程如下:
Private Sub CmdCircle_Click() '循环法
Dim s1,s2,s,k,d As Long '定义各变量为长整型
Dim i As Integer '定义循环变量即级数为整型数
s1 = 1 '第一级1
s2 = 2 '第二级2
s = 4 '第三级4
For i = 4 To 18
k = s2 '保存头3级的值
d = s '保存头2级的值
s = s + s1 + s2 '头级的值参与运算
s1 = k '放入头2级的值
s2 = d '放入头3级的值
Next i
TxtOutput.Text = "循环法结果:" + Str(s) '输出
End Sub
方法二:递归法解牛顿的问题
我们再对上面的规律进行一下分析,会觉得该规律非常有趣,如同我们常听的一个故事:
山上有座庙,庙里有个老和尚,老和尚在讲故事。它讲的故事是,山上有座庙,庙里有个老和尚,老和尚在讲故事。它讲的故事是:……
故事中包含了故事本身。这不正是我们的递归吗?好了,就用它,上面的牛顿上楼梯的故事可描述如下:1、2、3级时分别是1、2、4种走法,从第5级开始,是前面三级的和,下面就是对“老和尚讲故事”的定义:
'递归法计算函数
Function Newrec(ByVal x As Integer) As Long '函数Newrec,参数x为整型,返回值为长整型,Newrec这个函数可能是用来返回新记录的。
If x <= 1 Then x = 1
If x = 1 Then Newrec = 1 '第一级1
If x = 2 Then Newrec = 2 '第二级2
If x = 3 Then Newrec = 4 '第三级4
If x >= 4 Then '第4阶及以后是前面三级的和
Newrec = Newrec(x - 1) + Newrec(x - 2) + Newrec(x - 3)
End If
End Function
而我们的主程序十分简洁,只有一个输出语句,将上面的函数调用并输出就OK了。
Private Sub CmdRecirsion_Click()
TxtOutput.Text = "递归法结果是:" + Str(Newrec(18)) '调用函数输出
End Sub
(以上程序在VB6.0、Windows200下调试成功)
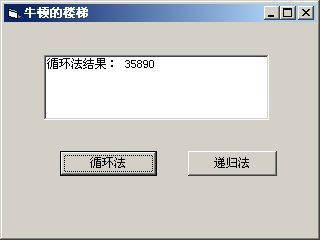
程序界面
界面非常简单,建立一标准EXE工程,其caption设为“牛顿的楼梯”,并加入两个命令按钮,将名称属性改为CmdRecirsion和CmdCircle,并将caption改为“递归法”和“循环法”,并在窗体上加一文本框TxtOutput,一切OK。我们将代码加给命令按钮_Click()(即各按钮的单击事件),将来运行时,我们只要用鼠标单击一下按钮,程序就执行相应的部分了。
一点补充
大家不妨在自己的机器上试试该程序,但要注意递归有时会了现栈溢出的问题,运行时的情况如图1所示。
从结果中我们不难看到,不论循环还是递归,得到的结果都是一样的。