趣味数学编程题解之两支蜡烛燃烧时间
IT商界
从上一篇《车牌号码之谜》中我们不难看出循环的重要作用,只要向电脑下一个命令,它就会“孜孜不倦”地执行了一万次。这种简洁的形式为我们解决趣味题中的多样性提供了可能。只要将循环这种形式掌握了,解决起趣味题来应该不难。
为了更好地在题目中应用循环这种形式,下面再对这种形式进行一下详细的研究。
循环有几种重要的形式,For循环只是循环的一种形式,这种形式的条件比较呆板,也比较好用。其实循环还有其他的形式,下面的题目,将通过另外一种循环形式来解决问题。通过对两种循环形式的比较,加深我们对该语句的理解,以便更好地来处理问题。
题目是苏联的著名数学家R·H·别莱利曼写的,他还是一位杰出的科普作家,在他的书中写过不少有意思的题目,下面的这道题目,是比较简单的一个,我们用编程方法来解一下看看。
题目:两支蜡烛
房间里电灯突然熄灭:保险丝烧断了。我点燃了书桌上备用的两支蜡烛,在蜡烛光下继续做我的工作,直到电灯修好。
第二天,需要确定昨晚断电共有多长时间。我当时没有注意断电开始的时刻,也没有注意是什么时候来的电。我也不知道蜡烛的原始长度。我只记得两支蜡烛是一样长短的,但粗细不同,其中粗的一支能用5小时(完全用完),细的一支4个小时用完。两支蜡烛都是经我点燃的新烛。我没找到蜡烛的剩余部分──家里人把它扔掉了。
──残烛几乎都烧光了,已不值得保留──家里人这样回答。
──你能记得残余部分有多长吗?
──两支蜡烛不一样。一支残烛的长度等于另一支残烛的四倍。
我无法知道得更多了,只好以上述资料为限,据此算出蜡烛的点燃时间。
如果是你,你应该怎样摆脱这个困境?
问题分析
两支蜡烛是同时点燃的,又是同时熄灭的,让我们根据其剩余尺寸的比例来判断它们究竟燃烧了多长时间,这就是题目所要的结果。但详细读一下题目,好像不确定的东东太多,那只有一点点来挖掘了。
要求出点燃的时间,我们先看一下时间的范围,范围是我们可估计出的,在0~4小时之间,但不可能是0或4,因为不可能是在没有燃烧时间的情况下(0)或者是有一支燃尽的情况下(4)发生题目中出现的现象,那究竟是经过多长时间它们被熄灭的呢?
最后熄灭时的条件是:一支残烛的长度等于另一支残烛的四倍。将这个条件再描述得详细一点,即粗的一支的长度是细的一支的四倍,这就是条件。故事虽然很长,给我们的编程信息只有这些。
处理过程详细说明
既然是在0~4小时中的某一时刻,我们可以通过循环来经过这个时间段的分分秒秒,然后在那每一个瞬间看是不是符合最后熄灭的条件。这种结构自然在程序的外部是一个循环语句,循环的增长值必须选择得足够小,不然可能会错过那个点或离实际的值太远。我们将这个时刻定义为X。可以通过For循环来完成,设一个足够小的步长值。
而什么时候我们没必要再继续下去呢?当符合上述的熄灭条件时。用语言来描述,条件就是这样的:
1-X/5=4*(1-X/4)
从上面的表达式中我们可以看到,两边得到的值可能都是小数,正是因为小数的存在,在计算的过程中等式两边很难出现完全相等的情况。所以我们最好通过另外一种循环的形式加以解决,即While循环的形式。这样,对于运算过程中出现的误差比较容易把握。
While语句和For语句有点相似,但又各有特点。
For 一般用于循环次数已知的循环,While则用于循环次数未知的循环,或者说循环的次数正是我们的所求。对于For的条件,例如:i=1 to 100,从这个条件中我们很容易判断其执行了100次,这个条件全部写完整如下:
i=1 to 100 step 1
也就是i从1递增到100,每次增加一个值,并且包括1和100,通过计算不难得到是100次。
While的条件则仅仅是一个表达式,当符合表达式的条件时就进入循环,不符合则退出。所以如果不前后进行联系,很难判断循环究竟执行了多少次。二者的具体形式如下:
(1)For 的形式
For 条件
循环体
Next
(2)While的形式
While 条件
循环体
Wend
For的条件比较好控制,从一个量到另一个量,次数通过量与量的大小差就可计算。
While的条件不能决定其循环究竟可执行多少次,但可在内部循环体中对它进行控制,以达到循环次数最终也是确定的。
所以通过For和While循环的特点,本题中还是选择While比较合适,条件是什么呢?从蜡烛的长短关系上,选择:1-x/5<4*(1-X/4)比较合适。
为什么不选择1-X/5>4*(1-X/4)的情况呢?再就是=号是不是需要加上呢?
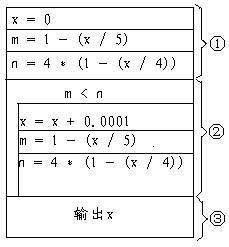
这要在X所在的范围0-4小时内对比关系运算符两边的值的大小情况,在他们的相等点之前,前面的值要小,在相等值之后,后面的值要小,而我们找的是相等点,只有从小到大,到相等的时候结束。所以选择了<符号。=在本题中无大影响,最多相差0.0001小时,可以忽略不计。其N—S图如图所示,图从整体上可分为如图所示的三部分。
动手做程序
(1)语言
程序中通过Virual BASIC6.0语言来实现。
(2)界面
界面非常简单,建立一标准EXE工程,其caption设为“两支蜡烛”。然后在窗体上放入一个文本框控件,其名称改为txtlist,将text属性改为“”,再在窗体上放一命令按钮,其属性name为cmdlist,caption为“计算”。一切OK。我们将代码加给cmdlist_Click()即按钮的单击事件,将来运行时我们只要用鼠标单击一下窗体,程序就执行了。
(3)源程序
从图中我们不难看到,程序的主要代码大体可分成三部分。
Option Explicit
Private Sub CmdSearch_Click()
Dim x As Single '记录燃烧的每一时刻
Dim m, n As Single
‘主要代码如下
‘①部分
X = 0
m = 1 - (X / 5)
n = 4 * (1 - (X / 4))
‘②部分,整体结构是循环
While m < n '对每一个很小的时间间隔进行判断
X = X + 0.0001 '每次增加的很小的时间间隔
m = 1 - (X / 5)
n = 4 * (1 - (X / 4))
Wend
‘③部分,输出
TxtList.Text = "两支蜡烛燃烧的时间是:" + Str(x) ’输出结果
‘上面是主要代码
End Sub
(上程序在VB6、Win2000下调试通过)
注:本题的输出结果放在文本框中,而不是像第一期中那样直接输出到窗体上。
编程小结
运行一下,结果出来了,两支蜡烛燃烧的时间是:3.750022 。代入等式两边,结果还可以,误差比较小,就是它。
条件就在题目中,挖出得越多,编程就越容易。本题中虽然看似条件模糊,实际上已经隐藏在其中了,这可能是这个题目有意思的地方之一吧。