用Authorware绘制椭圆
软件世界
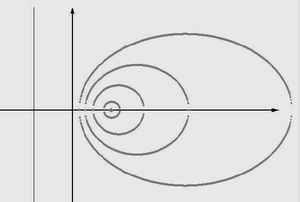
在高中数学解析几何中,椭圆的离心率的变化对椭圆形状的影响始终是一个难点。当初在教这个知识点的时候,费了我不少的口舌,可是学生却依旧似懂非懂。如果借助Authorware本身的系统函数和编程功能,我们可以很轻松地画出不同离心率情况下椭圆的形状,你的教学当然也会变得轻松了。
一、实现思路
我们知道,平面上到一定点的距离与到一定直线的距离之比为常数(大于0而小于1)的点的轨迹即椭圆。而这个常数其实就是椭圆的离心率。我们可以在屏幕上先设定定点和一定直线,然后根据上述椭圆离心率的定义,得到一个与离心率相关的椭圆上点的坐标计算公式,从而画出椭圆。利用循环过程,可依次画出离心率由小到大的不同椭圆。
二、实现过程
打开Authorware,新建一个文件,然后在流程线上拖一个计算图标,命名为“画椭圆”(做此课件,只要这一个图标就可以了)。双击这个计算图标,打开其输入窗口,在其中输入以下内容(【】中为注释内容):
h:=200
k:=240 【这两句的作用是设置椭圆的中心(即坐标系的坐标原点)在屏幕上的位置。屏幕左上角的坐标是(0,0)。h和k的值可以根据需要进行设置。】
SetLine(2) 【这个函数的作用是设置画线的方式:末端带箭头。】
Line(1,h-300,k,h+400,k)
Line(1,h,k+200,h,k-200) 【过屏幕上点(h,k)画两条相互垂直的带有箭头的直线,以此来代表直角坐标系中的横轴和纵轴。】
SetLine(0) 【这个函数的作用是设置画线的方式:不带箭头。】
Line(1,h-75,k-200,h-75,k+200) 【画一条直线表示椭圆概念中的“定直线”。此处的直线方程为x=-3。即在所作的坐标系中屏幕上每25个像素代表直角坐标系中一个单位长度。】
SetFill(1,RGB(255,0,0))
SetFrame(1,RGB(255,0,0)) 【这两个函数的作用是设置用红色的边框线画图,并用红色填充。】
Circle(2,h+75-4,k-4,h+75+4,k+4) 【画一个小圆表示椭圆概念中“定点”。此处定点在坐标系中的坐标是(3,0)】
a:=0.1【设置离心率的初值是0.1】
repeat while a<0.8
x:=25*(-3*(a-1)**2/(a**2-1)) 【设置画椭圆时x的初值。此处x的初值应当由所求得的椭圆方程计算得到。】
repeat while x<=25*(-3*(a+1)**2/(a**2-1)) 【设置循环的条件。此处x的最大值也应由所求得的椭圆方程计算得到。其实初值和最大值之间的值正是x的取值范围。】
y:=SQRT((a**2-1)*(x/25)**2+6*(a**2+1)*(x/25)+9*(a**2-1))*25+k【这就是我们得到在离心率为a的情况下椭圆上每一点坐标的计算公式。】
Circle(1,x+h-2,y-2,x+h+2,y+2) 【在每一点的坐标处画一个小圆代表轨迹上的点】
y:=-SQRT((a**2-1)*(x/25)**2+6*(a**2+1)*(x/25)+9*(a**2-1))*25+k
Circle(1,x+h-2,y-2,x+h+2,y+2) 【以上两句是y为负值的情况。仍旧是以画圆代表轨迹上的点】
x:=x+1
end repeat
a:=a+0.2【设置循环的频率,为画下一个椭圆设置离心率a值。】
end repeat【当满足条件后,结束循环。】
然后,保存(如果弹出对话框要求你设置变量的话,那么点“确认”即可。别的什么也甭做)。执行一下即大功告成(如(图1)所示),是不是很生动形象。